Non-classical logic challenges traditional binary frameworks by incorporating alternative truth values and reasoning methods, extending beyond true and false. This approach addresses paradoxes, uncertainty, and inconsistency, enhancing fields such as computer science and philosophy. Explore the rest of the article to discover how non-classical logic transforms problem-solving and decision-making.
Table of Comparison
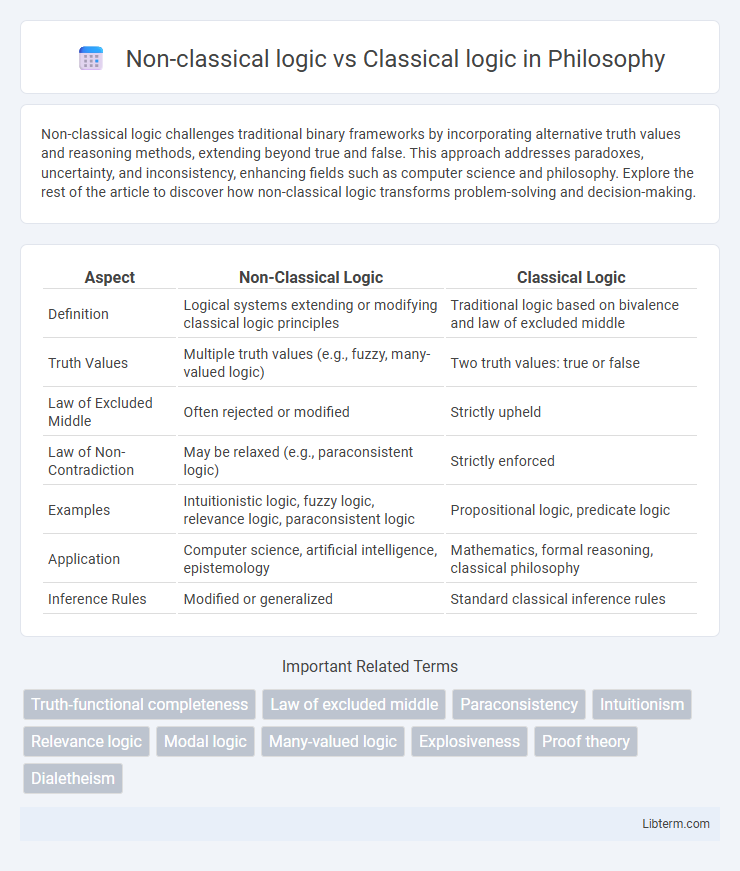
| Aspect | Non-Classical Logic | Classical Logic |
|---|---|---|
| Definition | Logical systems extending or modifying classical logic principles | Traditional logic based on bivalence and law of excluded middle |
| Truth Values | Multiple truth values (e.g., fuzzy, many-valued logic) | Two truth values: true or false |
| Law of Excluded Middle | Often rejected or modified | Strictly upheld |
| Law of Non-Contradiction | May be relaxed (e.g., paraconsistent logic) | Strictly enforced |
| Examples | Intuitionistic logic, fuzzy logic, relevance logic, paraconsistent logic | Propositional logic, predicate logic |
| Application | Computer science, artificial intelligence, epistemology | Mathematics, formal reasoning, classical philosophy |
| Inference Rules | Modified or generalized | Standard classical inference rules |
Introduction to Classical and Non-Classical Logic
Classical logic is based on principles such as the law of excluded middle and law of non-contradiction, ensuring every proposition is either true or false. Non-classical logic challenges these principles by introducing alternative frameworks like modal logic, fuzzy logic, or intuitionistic logic to handle concepts like uncertainty, vagueness, or incomplete information. These variations expand the scope of logical reasoning beyond classical binary constraints and better accommodate real-world complexities.
Historical Development of Logic Systems
Classical logic, rooted in Aristotle's syllogistic reasoning and formalized through Frege's predicate logic in the 19th century, established the foundation of truth-functional systems based on bivalence and the law of excluded middle. Non-classical logic emerged in the 20th century, driven by the need to address limitations in classical frameworks, introducing systems like modal logic, intuitionistic logic, and fuzzy logic that reject or modify classical principles to handle concepts such as uncertainty, possibility, and constructivism. The historical development of logic systems reflects a progression from absolute binary truth values toward more flexible and context-sensitive approaches, enabling advancements in mathematics, computer science, and philosophical logic.
Fundamental Principles of Classical Logic
Classical logic is grounded in fundamental principles such as the law of excluded middle, which asserts that every proposition is either true or false, and the law of non-contradiction, which prohibits a statement from being both true and false simultaneously. It operates on bivalent truth values and employs rigid inference rules like modus ponens to ensure consistency and completeness. Non-classical logic, by contrast, challenges these principles by allowing for multiple truth values, paraconsistency, or contextual interpretations to address limitations in classical frameworks.
Key Variants of Non-Classical Logic
Non-classical logic includes key variants such as modal logic, which introduces necessity and possibility operators, intuitionistic logic that rejects the law of excluded middle, and fuzzy logic allowing truth values between true and false. These variants address limitations of classical logic by handling ambiguity, uncertainty, and incomplete information more effectively. Their applications span computer science, artificial intelligence, and philosophical reasoning, enhancing problem-solving beyond classical frameworks.
Differences in Truth Values and Semantics
Non-classical logic extends beyond the binary true/false evaluation of classical logic by incorporating multiple or graded truth values, such as in fuzzy logic or intuitionistic logic, where truth can be uncertain or partial. Classical logic relies on bivalent semantics with strict laws like the law of excluded middle and non-contradiction, whereas non-classical logic often rejects or modifies these laws to handle vagueness, uncertainty, or incomplete information. The semantic frameworks of non-classical logics are designed to capture more nuanced interpretations of propositions, enabling reasoning in contexts where classical logic's rigid true/false dichotomy is insufficient.
Applications in Mathematics and Philosophy
Non-classical logic extends or modifies principles of classical logic, enabling the treatment of propositions involving uncertainty, vagueness, and paradoxes, which are crucial in advanced mathematical theories and philosophical inquiries. In mathematics, non-classical logics such as intuitionistic logic and fuzzy logic support constructive proofs and approximate reasoning, facilitating developments in topology, computer science, and formal verification. Philosophical applications of non-classical logic address the limitations of classical binary truth values, providing frameworks for modal logic, relevance logic, and many-valued logics that explore necessity, belief, and ethical reasoning.
Handling Contradictions: Classical vs Non-Classical Approaches
Classical logic strictly adheres to the law of non-contradiction, rejecting any statement that is simultaneously true and false, leading to triviality if contradictions occur. In contrast, non-classical logics such as paraconsistent logic allow conflicting statements to coexist without collapsing the system, enabling reasoning in the presence of inconsistencies. This approach is particularly useful in fields like knowledge representation and artificial intelligence, where real-world data often contains contradictory information.
Relevance in Computer Science and Artificial Intelligence
Non-classical logic, including modal, fuzzy, and relevance logics, addresses limitations of classical logic by incorporating uncertainty, partial truth, and context-sensitive inference, which are crucial for modeling real-world scenarios in Artificial Intelligence. Classical logic's rigid true/false dichotomy often fails in complex AI tasks such as reasoning, knowledge representation, and automated theorem proving, where non-monotonic reasoning and paraconsistency improve robustness and flexibility. Relevance logic specifically enhances computational efficiency by ensuring that only pertinent premises influence conclusions, optimizing algorithms in fields like natural language processing and expert systems.
Strengths and Limitations of Each Logic Type
Non-classical logic, including modal, fuzzy, and intuitionistic variants, excels in handling uncertainty, vagueness, and incomplete information, making it ideal for real-world applications like AI and decision theory, but it often lacks the universal applicability and simplicity of classical logic. Classical logic, characterized by binary truth values and well-established inference rules, provides a solid foundation for mathematics and computer science with clear, unambiguous reasoning, yet it struggles to model phenomena involving ambiguity or partial truth. The trade-off involves classical logic's precision and generality versus non-classical logic's flexibility and expressiveness in complex or uncertain contexts.
Future Directions in Logic Research
Future directions in logic research emphasize the integration of non-classical logic systems, such as intuitionistic, modal, and quantum logics, to address limitations of classical logic in dealing with uncertainty, vagueness, and dynamic information. Advances in computational logic are driving the development of hybrid frameworks that combine classical and non-classical principles, enhancing automated reasoning, artificial intelligence, and formal verification. Emerging research explores the applicability of non-classical logics in distributed systems, causal inference, and knowledge representation, aiming to create more robust and adaptable logical models for complex real-world problems.
Non-classical logic Infographic
 libterm.com
libterm.com