The contrapositive of a conditional statement reverses and negates both the hypothesis and conclusion, making it logically equivalent to the original statement. Understanding contrapositives is essential in mathematics and logic to prove statements more effectively by transforming complex assertions into simpler forms. Explore the article to discover how contrapositives enhance your reasoning and problem-solving skills.
Table of Comparison
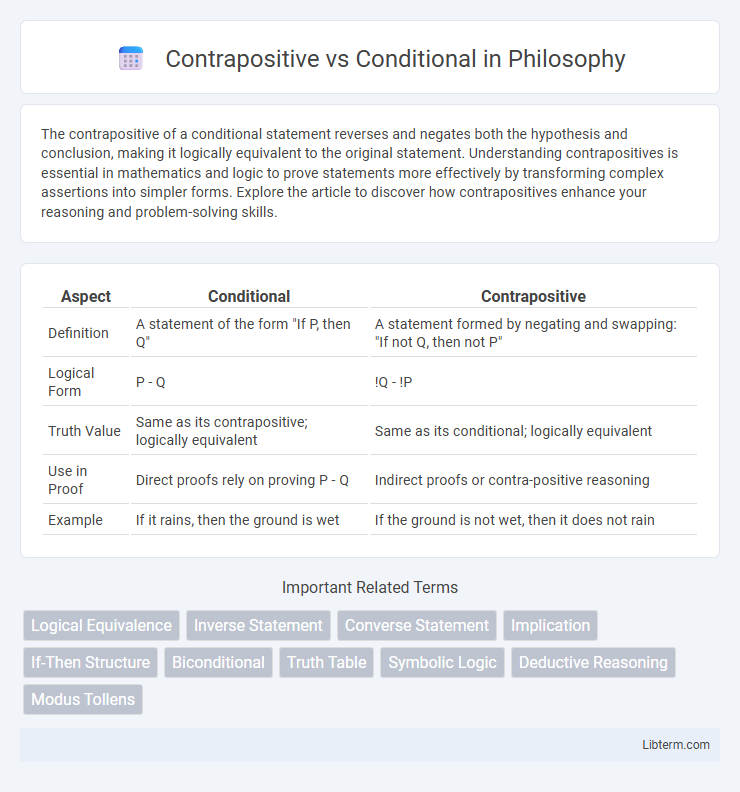
| Aspect | Conditional | Contrapositive |
|---|---|---|
| Definition | A statement of the form "If P, then Q" | A statement formed by negating and swapping: "If not Q, then not P" |
| Logical Form | P - Q | !Q - !P |
| Truth Value | Same as its contrapositive; logically equivalent | Same as its conditional; logically equivalent |
| Use in Proof | Direct proofs rely on proving P - Q | Indirect proofs or contra-positive reasoning |
| Example | If it rains, then the ground is wet | If the ground is not wet, then it does not rain |
Introduction to Conditional Statements
Conditional statements express a logical relationship where if a hypothesis is true, then a conclusion follows, typically written as "If P, then Q." The contrapositive of a conditional statement reverses and negates both parts, forming "If not Q, then not P," which is logically equivalent to the original. Understanding the structure and equivalence between these forms is crucial in mathematical proofs and logical reasoning.
Defining Contrapositive in Logic
The contrapositive of a conditional statement "If P, then Q" is logically equivalent to "If not Q, then not P," reversing and negating both the hypothesis and conclusion. In formal logic, this transformation preserves truth values, making the contrapositive a vital tool for proof techniques and logical deductions. Understanding the contrapositive enhances reasoning by confirming the equivalence between a conditional statement and its negated converse.
Key Differences Between Conditional and Contrapositive
A conditional statement follows the format "If P, then Q," establishing a direct relationship between condition P and consequence Q. The contrapositive of this statement reverses and negates both parts, resulting in "If not Q, then not P," which is logically equivalent to the original conditional. Understanding this key difference is crucial for valid logical reasoning and proofs, as the truth of the contrapositive guarantees the truth of the conditional statement.
Truth Values: How Contrapositives Work
The contrapositive of a conditional statement \( p \rightarrow q \) is \( \neg q \rightarrow \neg p \), and both share identical truth values, making them logically equivalent. When the original conditional is true, its contrapositive must also be true because the falsity of \( q \) guarantees the falsity of \( p \). This equivalence is fundamental in mathematical proofs and logic, enabling the validation of statements by proving their contrapositives.
Symbolic Representation: Conditional vs Contrapositive
The conditional statement is symbolically represented as \(p \to q\), meaning "if \(p\), then \(q\)." Its contrapositive is represented as \(\neg q \to \neg p\), which logically holds the same truth value as the original conditional. Understanding the symbolic form of the contrapositive is crucial in mathematical proofs and logic, as it provides an equivalent expression to the conditional statement that often simplifies reasoning.
Real-world Examples of Conditional Statements
Conditional statements often appear in daily decision-making, such as "If it rains, then the ground will be wet." The contrapositive of this statement, "If the ground is not wet, then it does not rain," remains logically equivalent and is used in scientific hypotheses or troubleshooting processes. In fields like computer programming, understanding conditional and contrapositive logic helps developers debug code by testing outcomes under specific conditions.
Constructing the Contrapositive: Step-by-Step Guide
Constructing the contrapositive involves first identifying the conditional statement's hypothesis (p) and conclusion (q). Next, negate both the hypothesis and conclusion, forming !q - !p. This process ensures logical equivalence between the original conditional statement and its contrapositive, preserving truth values in formal logic.
Importance in Mathematical Proofs
Understanding the contrapositive is crucial in mathematical proofs because it allows for the equivalence transformation of a conditional statement "If P, then Q" into "If not Q, then not P," preserving truth values and simplifying logical reasoning. Employing contrapositives often makes proving implications more straightforward, especially when direct proof of the original conditional is complex. Mastery of this logical equivalence enhances precision and efficiency in constructing valid mathematical arguments.
Common Misconceptions and Errors
Common misconceptions about contrapositive and conditional statements often involve confusing their truth values; many erroneously believe that a conditional statement and its converse are logically equivalent, though only the contrapositive shares the same truth value as the original conditional. Another frequent error is assuming the contrapositive negates the hypothesis and conclusion without reversing them, which misrepresents its logical structure: the contrapositive of "If P, then Q" is correctly expressed as "If not Q, then not P." Misunderstanding these relationships leads to flawed reasoning in proofs and arguments, underscoring the importance of correctly identifying and applying contrapositive statements in logical deduction.
Summary and Practical Applications
The contrapositive of a conditional statement reverses and negates both its hypothesis and conclusion, preserving logical equivalence and ensuring that if the conditional is true, its contrapositive is also true. In practical applications, understanding this relationship aids in mathematical proofs, computer science algorithms, and logical problem-solving by allowing alternative approaches to validate statements or identify contradictions. Mastery of contrapositive reasoning enhances critical thinking and decision-making in fields such as formal logic, software development, and analytical reasoning.
Contrapositive Infographic
 libterm.com
libterm.com