The associative property states that the way numbers are grouped in addition or multiplication does not affect the result, meaning (a + b) + c = a + (b + c) for addition and (a x b) x c = a x (b x c) for multiplication. This property simplifies complex calculations by allowing flexible grouping of terms without changing the outcome. Explore the rest of the article to understand how the associative property applies to different mathematical operations and practical examples.
Table of Comparison
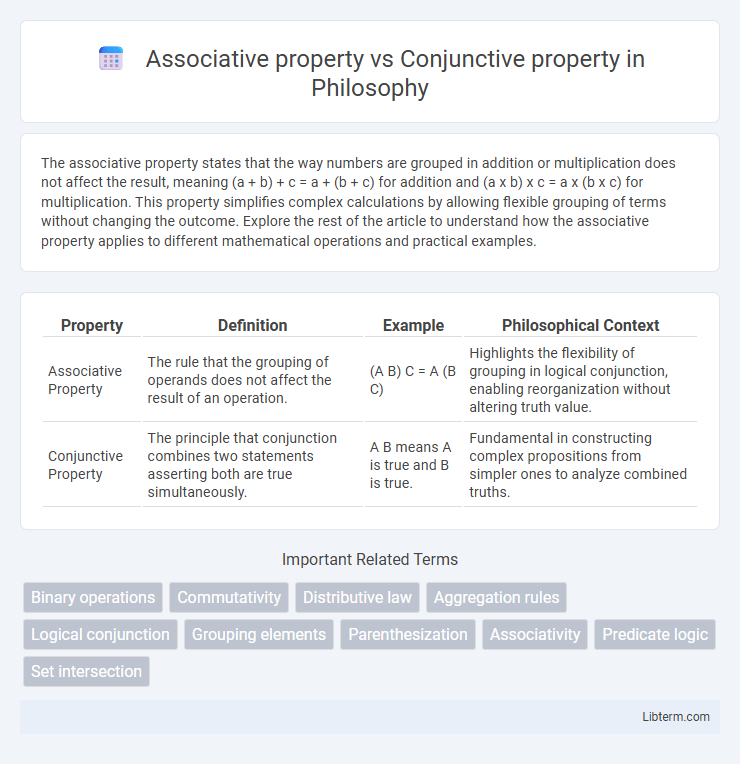
| Property | Definition | Example | Philosophical Context |
|---|---|---|---|
| Associative Property | The rule that the grouping of operands does not affect the result of an operation. | (A B) C = A (B C) | Highlights the flexibility of grouping in logical conjunction, enabling reorganization without altering truth value. |
| Conjunctive Property | The principle that conjunction combines two statements asserting both are true simultaneously. | A B means A is true and B is true. | Fundamental in constructing complex propositions from simpler ones to analyze combined truths. |
Understanding the Associative Property
The associative property in mathematics states that the way numbers are grouped in addition or multiplication does not affect the result, such as (a + b) + c = a + (b + c). This property is fundamental in simplifying expressions and performing calculations efficiently by regrouping terms without changing the outcome. In contrast, the conjunctive property is not a standard mathematical term, making the associative property a key concept for understanding operational consistency in arithmetic and algebra.
Defining the Conjunctive Property
The conjunctive property refers to the logical principle where two or more conditions must all be true simultaneously for a compound statement to be true, represented by the logical AND operator. Unlike the associative property, which deals with the grouping of elements without changing the outcome in operations like addition or multiplication, the conjunctive property emphasizes the necessity of every component condition being satisfied in logical conjunctions. This property is fundamental in mathematical logic, computer science, and set theory for constructing precise and reliable compound statements.
Key Differences Between Associative and Conjunctive Properties
The associative property refers to the rule in mathematics where the grouping of numbers does not affect the sum or product, such as (a + b) + c = a + (b + c), whereas the conjunctive property relates to logic, where a conjunction (AND operation) is true only if both conditions are true simultaneously. Key differences include their domains--associative property applies primarily in arithmetic and algebra, while conjunctive property is used in propositional logic. Additionally, the associative property involves rearranging parentheses without changing outcomes, whereas the conjunctive property focuses on the truth values of combined statements.
Mathematical Examples of Associative Property
The associative property in mathematics states that the way numbers are grouped in addition or multiplication does not affect the result, as shown by examples like (2 + 3) + 4 = 2 + (3 + 4) and (5 x 6) x 2 = 5 x (6 x 2). This property applies specifically to operations such as addition and multiplication, allowing for flexible grouping without changing the sum or product. Unlike the associative property, the conjunctive property is not a standard mathematical term and generally does not describe grouping or operational equivalences in arithmetic.
Mathematical Examples of Conjunctive Property
The conjunctive property in mathematics is demonstrated when two statements or conditions are combined using the logical AND operator, such as "x > 2 AND y < 5," ensuring both must be true simultaneously. For example, the system of inequalities x + y = 10 AND x - y = 4 shows two conditions that must hold together for a solution to exist. Unlike the associative property, which deals with the grouping of operations like (a + b) + c = a + (b + c), the conjunctive property emphasizes the simultaneous truth of multiple statements.
Importance in Algebraic Operations
The associative property is crucial in algebra as it allows the grouping of terms without changing the result, simplifying complex expressions and enhancing calculation efficiency. The conjunctive property, often linked to logic and set theory, emphasizes the combination of conditions or elements, playing a vital role in solving equations with multiple constraints. Mastery of these properties supports accurate manipulation of algebraic expressions and effective problem-solving strategies in mathematics.
Role in Logical Reasoning
The associative property in logical reasoning allows the grouping of operands to change without affecting the outcome, enabling simplification and restructuring of logical expressions in proofs. The conjunctive property focuses on the use of conjunctions (AND operations) to combine statements, ensuring that all combined conditions must be true for the whole expression to hold. Together, these properties facilitate the manipulation and evaluation of logical statements by clarifying how components relate and combine within arguments.
Common Misconceptions
Confusion often arises between the associative and conjunctive properties due to their similar-sounding names, but the associative property deals with the grouping of elements in operations like addition or multiplication without changing the result, while there is no widely recognized "conjunctive property" in standard mathematics. A common misconception is mistaking the associative property for the commutative property, which actually involves the order of elements rather than grouping. Clarifying these distinctions is crucial for a proper understanding of fundamental algebraic principles.
Real-life Applications
The associative property, which states that the grouping of numbers does not affect the sum or product (e.g., (a + b) + c = a + (b + c)), is commonly applied in budgeting and financial planning where transactions are grouped for simplification. The conjunctive property, related to logic and set theory, involves the combination of conditions or sets where both must be true or satisfied, often used in database queries and decision-making processes. These properties streamline complex calculations and data filtering in fields such as computer science, finance, and logistics.
Summary and Key Takeaways
The associative property in mathematics describes how the grouping of numbers does not affect the sum or product, such as in addition and multiplication (e.g., (a + b) + c = a + (b + c)). The conjunctive property typically pertains to logic, emphasizing the combination of statements that must both be true simultaneously, expressed as "A and B" in propositional logic. Understanding the associative property's role in algebraic operations and the conjunctive property's function in logical expressions helps clarify their distinct applications in math and logic.
Associative property Infographic
 libterm.com
libterm.com