Tautology occurs when a statement repeats the same idea using different words, leading to redundancy without adding new information. It can weaken arguments by making them less concise and impactful, often causing confusion or boredom. Explore the rest of the article to understand how avoiding tautology can improve your communication skills.
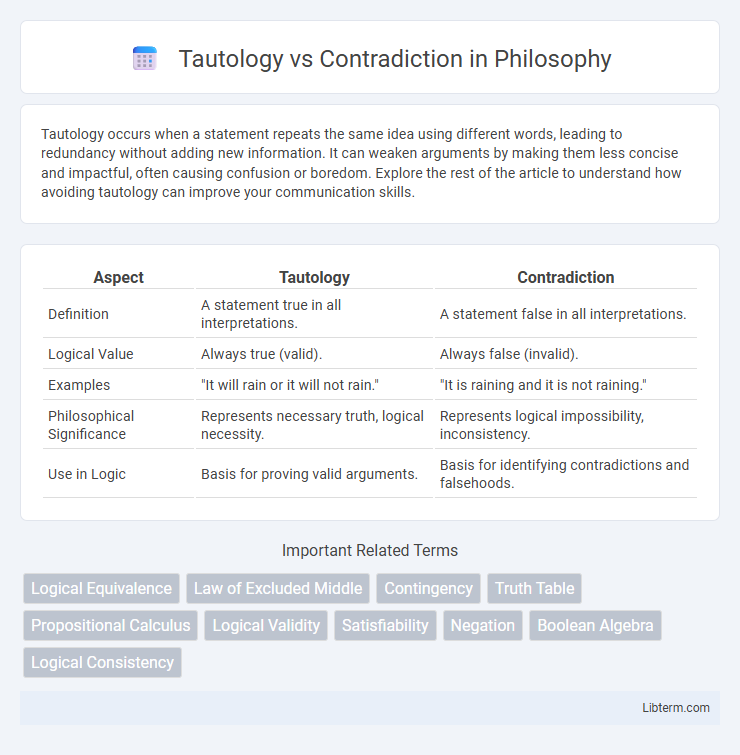
Table of Comparison
| Aspect | Tautology | Contradiction |
|---|---|---|
| Definition | A statement true in all interpretations. | A statement false in all interpretations. |
| Logical Value | Always true (valid). | Always false (invalid). |
| Examples | "It will rain or it will not rain." | "It is raining and it is not raining." |
| Philosophical Significance | Represents necessary truth, logical necessity. | Represents logical impossibility, inconsistency. |
| Use in Logic | Basis for proving valid arguments. | Basis for identifying contradictions and falsehoods. |
Introduction to Tautology and Contradiction
Tautology represents a statement in logic that is always true regardless of the truth values of its components, serving as a foundational concept in propositional logic and Boolean algebra. Contradiction, by contrast, is a logical statement that is always false, exemplifying inconsistency within logical expressions. Understanding tautologies and contradictions is critical for simplifying logical formulas, validating arguments, and developing algorithms in computer science and mathematics.
Defining Tautology in Logic
A tautology in logic is a formula or proposition that is universally true in every possible interpretation or valuation of its variables. It remains invariant under all truth assignments, guaranteeing an outcome of true regardless of the logical components involved. This concept is fundamental in propositional logic for evaluating the validity of logical statements and constructing proofs.
Understanding Contradiction in Logic
In logic, a contradiction occurs when a statement is inherently false under all possible interpretations, meaning it cannot be true in any circumstance. Contradictions are represented by formulas that evaluate to false regardless of the truth values of their components, such as (P !P). Understanding contradictions is crucial for identifying logical inconsistencies and establishing the validity of arguments by recognizing statements that cannot coexist logically.
Key Differences Between Tautology and Contradiction
Tautology is a logical statement that is always true regardless of the truth values of its components, while contradiction is always false under any interpretation. The key difference lies in their truth value consistency: tautology holds universal truth, whereas contradiction never holds true. Understanding these differences is crucial for logical proof construction and evaluating argument validity.
Importance in Propositional Logic
Tautology and contradiction are fundamental concepts in propositional logic that determine the validity and consistency of logical statements. A tautology is a formula that is true in every possible interpretation, making it a crucial tool for verifying logical proofs and ensuring sound reasoning. In contrast, a contradiction is a formula that is false in every interpretation, highlighting inconsistencies and errors within logical systems.
Examples of Tautologies
A tautology is a logical statement that is true in every possible interpretation, such as "It will rain or it will not rain," demonstrating its universal truth. Another example is the statement "Either the light is on or the light is off," which covers all logical possibilities without exception. These examples highlight tautologies as statements that cannot be false, in contrast to contradictions which are false in every interpretation.
Examples of Contradictions
Contradictions are logical statements that are always false regardless of the truth values of their components, such as "p !p," where "p" and "not p" cannot both be true simultaneously. Examples include formulas like "The sky is blue and the sky is not blue" or "It is raining and it is not raining at the same time." These contradictions violate the law of non-contradiction, making them essential in logic for identifying impossible or false conditions.
Real-Life Applications in Reasoning
Tautologies in real-life reasoning ensure statements or arguments are always true, providing a reliable foundation for logical decision-making and automated theorem proving systems. Contradictions identify inconsistencies within data sets or arguments, crucial for error detection in software debugging, legal reasoning, and database integrity checks. Using tautologies and contradictions enhances clarity and accuracy in critical thinking, enabling effective problem-solving and validation across various fields.
How to Identify Tautology and Contradiction
Identify a tautology by checking if a logical statement is true in every possible interpretation or truth value assignment, meaning it is universally valid in propositional logic. Detect a contradiction by determining if the statement is false under all truth value assignments, indicating it cannot be true in any scenario. Use truth tables or logical equivalences to systematically verify these properties for precise classification.
Conclusion: Significance in Logical Analysis
Tautologies represent statements that are always true, serving as foundational truths in logical proofs and ensuring the validity of arguments. Contradictions, which are statements always false, highlight inconsistencies and errors within reasoning, signaling invalid arguments. Understanding the distinction between tautology and contradiction is crucial for evaluating argument soundness and ensuring rigorous logical analysis.
Tautology Infographic
 libterm.com
libterm.com