Infinite possibilities exist when exploring the concept of infinity in mathematics and philosophy, stretching beyond finite understanding. This boundless nature challenges your perception of limits and encourages deeper contemplation of the universe. Dive into the article to uncover the fascinating dimensions of the infinite.
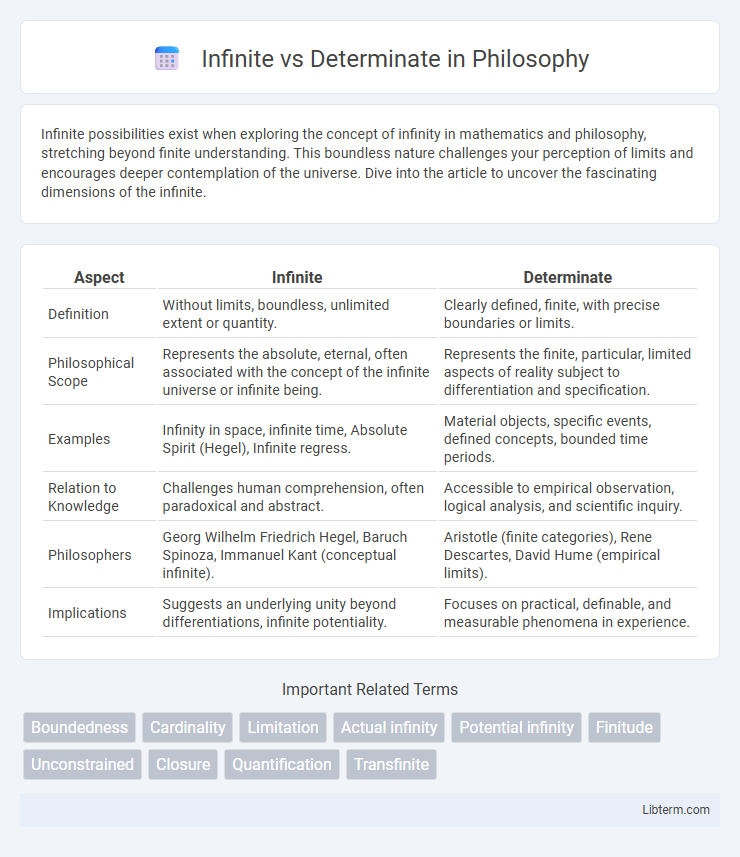
Table of Comparison
| Aspect | Infinite | Determinate |
|---|---|---|
| Definition | Without limits, boundless, unlimited extent or quantity. | Clearly defined, finite, with precise boundaries or limits. |
| Philosophical Scope | Represents the absolute, eternal, often associated with the concept of the infinite universe or infinite being. | Represents the finite, particular, limited aspects of reality subject to differentiation and specification. |
| Examples | Infinity in space, infinite time, Absolute Spirit (Hegel), Infinite regress. | Material objects, specific events, defined concepts, bounded time periods. |
| Relation to Knowledge | Challenges human comprehension, often paradoxical and abstract. | Accessible to empirical observation, logical analysis, and scientific inquiry. |
| Philosophers | Georg Wilhelm Friedrich Hegel, Baruch Spinoza, Immanuel Kant (conceptual infinite). | Aristotle (finite categories), Rene Descartes, David Hume (empirical limits). |
| Implications | Suggests an underlying unity beyond differentiations, infinite potentiality. | Focuses on practical, definable, and measurable phenomena in experience. |
Understanding Infinite and Determinate: Key Definitions
Infinite refers to something without any limits or end, often used in mathematics and philosophy to describe boundless quantities or concepts. Determinate means clearly defined, limited, or having exact boundaries, commonly applied in logic, law, and science to specify precise conditions or states. Understanding these key definitions helps distinguish between limitless possibilities and concrete, measurable criteria.
Historical Perspectives on Infinity and Determinacy
The concept of infinity has evolved from ancient Greek philosophers like Zeno and Aristotle, who viewed it as potential or actual infinity, to modern mathematics where infinity represents an abstract, unbounded quantity. Determinacy in logic and set theory emerged through the study of infinite games and descriptive set theory, particularly with contributions from mathematicians such as David Gale and Ronald Jensen in the 20th century. These historical developments highlight a shift from philosophical interpretations of infinity to rigorous formalizations of both infinite processes and determinate outcomes in mathematical frameworks.
Infinite vs Determinate in Mathematics
Infinite sets in mathematics contain an unending number of elements, such as the set of natural numbers, while determinate (finite) sets have a fixed, countable number of elements. The concept of infinity is fundamental in calculus, set theory, and number theory, where it distinguishes between countable and uncountable infinities. Determinate quantities allow precise enumeration and measurement, making them essential for combinatorics and discrete mathematics.
Philosophical Implications of Infinity and Determinacy
The philosophical implications of infinity and determinacy revolve around concepts of existence, knowledge, and reality's limits. Infinity challenges the notion of complete knowledge by introducing boundlessness, while determinacy emphasizes definable states and concrete outcomes essential for logical reasoning. Exploring these ideas informs metaphysics, epistemology, and the nature of the universe, highlighting tensions between endless potential and finite certainty.
Infinite Concepts in Science and Physics
Infinite concepts in science and physics explore quantities or entities without any bounds, such as the infinitely large size of the universe or the infinitely small scale of quantum particles. The mathematical notion of infinity is crucial in calculus and set theory, providing tools to describe unbounded behavior and continuity. Concepts like infinite divisibility of space and time challenge finite models, driving theories in cosmology and quantum mechanics to address the nature of infinite structures and phenomena.
Determinate States in Logic and Reasoning
Determinate states in logic and reasoning refer to well-defined conditions where propositions possess precise truth values, either true or false, enabling clear and unambiguous conclusions. These states contrast with infinite or indeterminate systems, providing a framework for rigorous proof construction and algorithmic decision-making. The concept underpins classical logic, ensuring decidability and consistency within mathematical and computational reasoning processes.
The Role of Infinity in Art and Literature
Infinity in art and literature serves as a powerful symbol to explore boundlessness, the eternal, and the unknowable. Works featuring infinite patterns, like M.C. Escher's tessellations or Jorge Luis Borges' stories, highlight themes of endlessness and infinite possibilities. This concept challenges finite human perception and invites deeper reflection on existence and the universe.
Real-World Applications: When to Use Infinite or Determinate Models
Infinite models are ideal for large-scale systems where resource constraints or limits are negligible, such as telecommunications networks or cloud computing, where customers or tasks can arrive without bound. Determinate models suit scenarios with fixed capacities or limited resources, like manufacturing lines or inventory systems, where the exact number of entities must be controlled and managed. Selecting between infinite or determinate models depends on the system's scalability, resource availability, and operational constraints to accurately predict performance and optimize efficiency.
Challenges in Interpreting Infinite and Determinate
Interpreting infinite concepts presents challenges such as paradoxes and the inability to fully comprehend unbounded sets or processes, often requiring abstract mathematical frameworks like calculus and set theory. Determinate concepts, while seemingly more concrete, face difficulties in defining precise boundaries and conditions, especially in complex systems with ambiguous or fuzzy parameters. Both infinite and determinate interpretations demand rigorous logical analysis to avoid misrepresentations in fields such as philosophy, mathematics, and computer science.
Future Directions: Bridging Infinite and Determinate Concepts
Future directions in bridging infinite and determinate concepts emphasize developing hybrid frameworks that integrate infinite potentialities with finite constraints, enabling scalable and adaptable models. Research explores formalizing transitions between determinate states and infinite possibilities through advanced mathematical structures such as category theory and topology. These approaches aim to enhance applications in artificial intelligence, dynamic systems, and computational theory by harmonizing determinacy with unbounded growth.
Infinite Infographic
 libterm.com
libterm.com