Nominalism challenges the existence of universal forms, arguing that only particular objects are real and that general terms are mere names without inherent meaning. This philosophy influences various fields such as metaphysics, epistemology, and the philosophy of language, shaping debates about the nature of reality and concepts. Explore the rest of this article to understand how nominalism impacts your perception of universals and particulars.
Table of Comparison
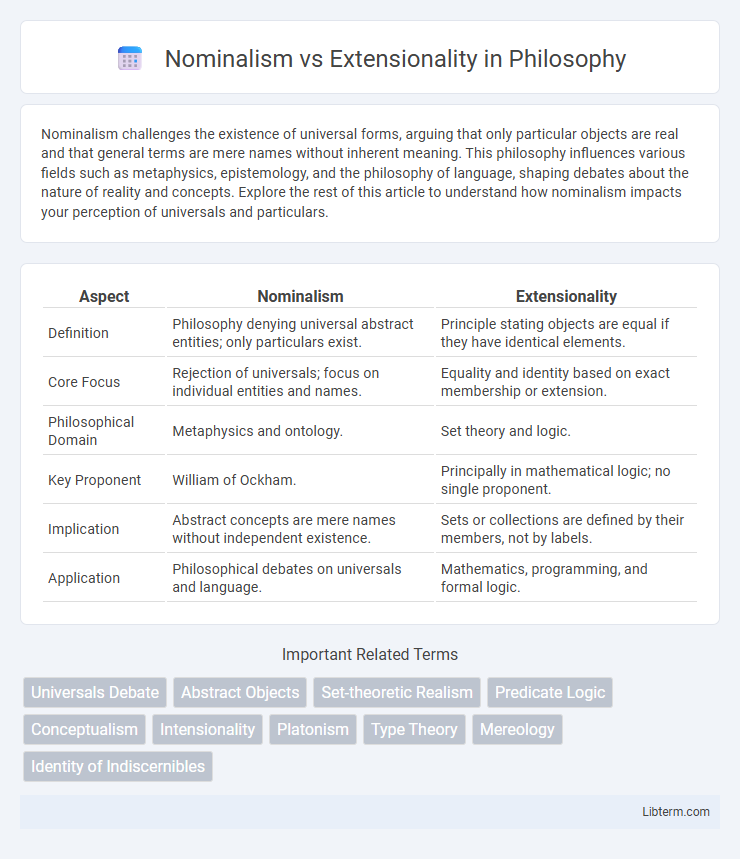
| Aspect | Nominalism | Extensionality |
|---|---|---|
| Definition | Philosophy denying universal abstract entities; only particulars exist. | Principle stating objects are equal if they have identical elements. |
| Core Focus | Rejection of universals; focus on individual entities and names. | Equality and identity based on exact membership or extension. |
| Philosophical Domain | Metaphysics and ontology. | Set theory and logic. |
| Key Proponent | William of Ockham. | Principally in mathematical logic; no single proponent. |
| Implication | Abstract concepts are mere names without independent existence. | Sets or collections are defined by their members, not by labels. |
| Application | Philosophical debates on universals and language. | Mathematics, programming, and formal logic. |
Introduction to Nominalism and Extensionality
Nominalism rejects the existence of abstract objects, asserting that only particular, concrete entities are real, while extensionality emphasizes the identity of sets based solely on their members. In philosophy and logic, nominalism challenges universals and abstract entities, focusing on individual instances instead. Extensionality, fundamental to set theory, dictates that two sets are equal if and only if they have precisely the same elements, highlighting the importance of membership over intrinsic properties.
Historical Background of Nominalism
Nominalism emerged in the late medieval period as a response to the debate on universals, challenging the existence of abstract entities independent of particular objects. Rooted in the works of philosophers like William of Ockham, it rejected the realist view that universals have an objective reality outside individual instances. This historical background positioned Nominalism as a foundation for later developments in logic, language theory, and the philosophy of science.
Foundations of Extensionality in Philosophy
Foundations of extensionality in philosophy emphasize the principle that objects or concepts are determined solely by their external properties and observable relations, contrasting with nominalism's rejection of abstract universals. Extensionality supports the view that mathematical and logical entities can be fully characterized by their membership or extension, promoting a clear, objective framework for semantic and ontological analysis. This foundation underpins formal systems in logic and mathematics by enabling precise criteria for identity and equality based on observable extensions rather than intrinsic or conceptual attributes.
Key Concepts and Definitions
Nominalism asserts that universals are merely names without independent existence, emphasizing individual objects as primary entities. Extensionality, chiefly in logic and set theory, defines equality by identical members or elements within sets or relations. These concepts diverge on whether abstract entities like properties have real existence or are simply linguistic constructs related to collections of objects.
Nominalism: Main Principles and Arguments
Nominalism asserts that universals and abstract objects do not exist independently of particular things, emphasizing that only individual entities are real. This position challenges extensionality by denying the existence of inherent properties shared among objects, arguing that such commonalities are mere names or linguistic constructs without ontological status. Nominalists argue that treating universals as real leads to metaphysical inflation, and their approach promotes a parsimonious ontology focused exclusively on concrete particulars.
Extensionality: Core Ideas and Theoretical Support
Extensionality asserts that the identity of sets is determined solely by their elements, emphasizing that two sets are identical if and only if they contain exactly the same members. This principle underpins classical set theory and supports the notion of extensional equality, which contrasts with nominalism's rejection of abstract objects. Foundational results in logic and mathematics, such as Zermelo-Fraenkel set theory, provide theoretical support for extensionality by formalizing how set membership defines set identity without invoking nominalistic constraints.
Comparative Analysis: Nominalism vs Extensionality
Nominalism asserts that universals or abstract concepts do not exist independently but are mere names without corresponding entities, emphasizing the specificity of individual objects. Extensionality, particularly in set theory and logic, defines equality of sets or functions based strictly on their elements or output values, disregarding any internal structure or naming conventions. Comparing Nominalism and Extensionality highlights a contrast between the rejection of abstract universals and the formal mathematical principle that identifies entities solely by their extensions or members.
Implications for Logic and Mathematics
Nominalism denies the existence of abstract entities, challenging the classical logical framework that relies on set theory and extensionality principles, which identify objects by their members. This perspective reshapes mathematical ontology by rejecting infinite sets as actual objects, impacting the interpretation of quantifiers and predicates in formal systems. Consequently, logic under nominalism favors syntactic or constructivist approaches, emphasizing concrete representations and avoiding commitment to abstract collections or extensional identity.
Criticisms and Challenges
Nominalism faces criticism for its inability to account for the objective existence of universals, leading to difficulties in explaining the commonalities between particular objects. Extensionality, especially in the context of set theory and logic, encounters challenges regarding the identity of indiscernibles and the treatment of intensional contexts. Both positions struggle with balancing ontological economy and explanatory power, sparking ongoing debates in metaphysics and the philosophy of language.
Contemporary Relevance and Applications
Nominalism's influence persists in contemporary philosophy of language and logic by emphasizing the rejection of abstract entities and focusing on concrete linguistic expressions, which informs theories in computational linguistics and artificial intelligence. Extensionality remains crucial in computer science and database theory, where the principle ensures that functions and predicates are defined solely by their output or extension, facilitating data consistency and optimization in query processing. Both concepts underpin semantic web technologies, enabling more precise ontology designs and improving automated reasoning systems' accuracy and interoperability.
Nominalism Infographic
 libterm.com
libterm.com