Intuitionistic logic rejects the law of excluded middle, emphasizing constructive proof where a statement is only true if there is a direct proof. This logic system is foundational in computer science and mathematics, particularly in type theory and proof verification. Explore the rest of the article to understand how intuitionistic logic shapes formal reasoning and computation.
Table of Comparison
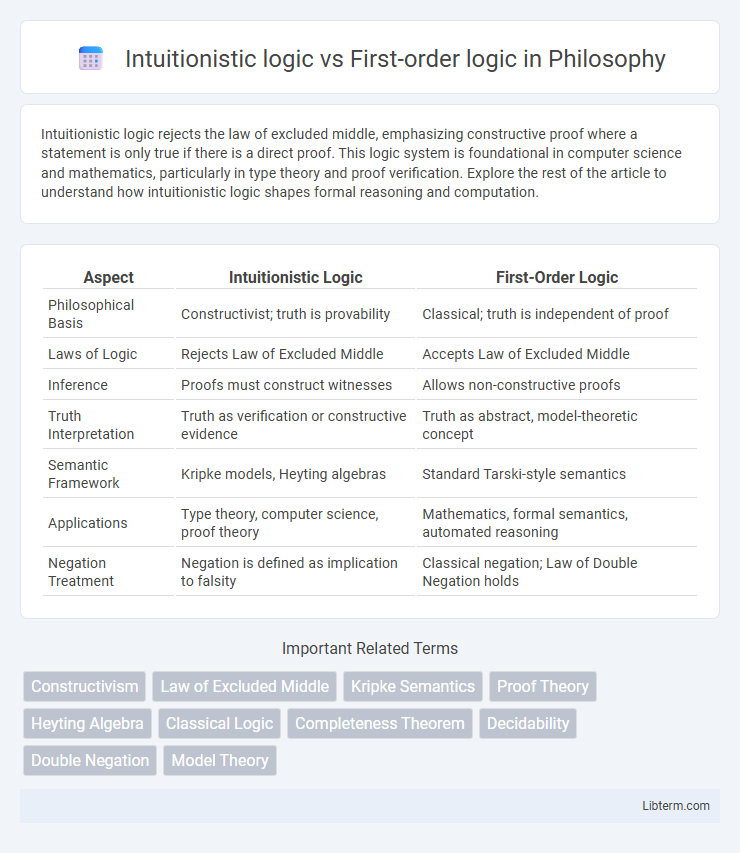
| Aspect | Intuitionistic Logic | First-Order Logic |
|---|---|---|
| Philosophical Basis | Constructivist; truth is provability | Classical; truth is independent of proof |
| Laws of Logic | Rejects Law of Excluded Middle | Accepts Law of Excluded Middle |
| Inference | Proofs must construct witnesses | Allows non-constructive proofs |
| Truth Interpretation | Truth as verification or constructive evidence | Truth as abstract, model-theoretic concept |
| Semantic Framework | Kripke models, Heyting algebras | Standard Tarski-style semantics |
| Applications | Type theory, computer science, proof theory | Mathematics, formal semantics, automated reasoning |
| Negation Treatment | Negation is defined as implication to falsity | Classical negation; Law of Double Negation holds |
Introduction to Intuitionistic Logic and First-Order Logic
Intuitionistic logic, rooted in constructive mathematics, emphasizes proof construction and rejects the law of excluded middle, contrasting with classical first-order logic which allows non-constructive proofs and includes this law. First-order logic provides a formal framework for quantification over individual variables with well-defined syntax and semantics, enabling analysis of properties and relations in mathematical structures. Intuitionistic logic modifies these foundations by restricting inference rules to preserve constructivity, impacting theorem proving and computational interpretations.
Core Principles: Constructivism vs Classical Reasoning
Intuitionistic logic emphasizes constructivism, requiring proof of existence through explicit construction and rejecting the law of excluded middle, which states that every proposition is either true or false. First-order logic, grounded in classical reasoning, accepts the law of excluded middle and allows reasoning based on indirect proof, including proof by contradiction. The fundamental difference lies in intuitionistic logic's demand for constructive proofs versus first-order logic's acceptance of non-constructive methods.
Syntax and Semantics: Key Differences
Intuitionistic logic differs from first-order logic primarily in its treatment of truth, where syntax restricts proofs to constructive evidence, rejecting the law of excluded middle and double negation elimination accepted in classical first-order systems. Semantically, intuitionistic logic employs Kripke models or Heyting algebras, emphasizing proof verification across possible worlds with an intuitionistic ordering, contrasting with classical first-order semantics grounded in Tarskian absolute truth valuations. These syntactic and semantic distinctions underscore intuitionistic logic's foundation in constructive mathematics, demanding explicit witness construction for existential statements and disallowing non-constructive proofs typical in first-order frameworks.
Proof Systems Compared: Natural Deduction and Hilbert Calculi
Intuitionistic logic and first-order logic differ significantly in their proof systems, particularly within Natural Deduction and Hilbert calculi frameworks. Intuitionistic natural deduction emphasizes constructivist proofs, avoiding the law of excluded middle, whereas first-order logic permits classical reasoning principles. Hilbert calculi for intuitionistic logic use axioms tailored to exclude non-constructive principles, contrasting with the classical axiomatic schema of first-order logic that includes classical tautologies.
Law of Excluded Middle: Acceptance and Rejection
Intuitionistic logic rejects the Law of Excluded Middle, asserting that a statement is only true if there is constructive proof, unlike first-order logic, which accepts the law as a fundamental principle allowing statements to be either true or false regardless of proof. This rejection by intuitionistic logic reflects its emphasis on proofs and constructive methods, contrasting with the classical, truth-valued semantics of first-order logic. The difference impacts proof theory and model theory, where intuitionistic logic requires explicit evidence for disjunctions and existential claims, while first-order logic permits nonconstructive arguments.
Quantifiers and Predicate Handling
Intuitionistic logic interprets quantifiers constructively, requiring explicit proof of existence for existential quantifiers and providing intuitionistic truth conditions for universal quantifiers, unlike classical first-order logic which relies on a bivalent truth valuation. Predicate handling in intuitionistic logic demands constructive evidence for predicates' satisfaction, reflecting a proof-oriented semantics rather than truth-functional evaluation typical in first-order logic. This fundamental difference affects model theory and proof systems, where intuitionistic logic's predicates and quantifiers align with constructive mathematics principles.
Applications in Mathematics and Computer Science
Intuitionistic logic underpins constructive mathematics and type theory, enabling proof systems that guarantee computable witnesses useful in automated theorem proving and programming language design. First-order logic serves as the foundation of classical mathematics, supporting model theory and formal verification by expressing and analyzing properties across structures. Computer science leverages intuitionistic logic in functional programming languages like Haskell and Coq, while first-order logic is extensively applied in database theory, artificial intelligence, and verification of hardware and software systems.
Expressive Power and Limitations
Intuitionistic logic restricts the law of excluded middle, leading to a constructive interpretation that limits some classical equivalences found in first-order logic, affecting its expressive power. While first-order logic fully supports classical semantics enabling a broader range of quantifications and negations, intuitionistic logic emphasizes proof construction and verification, which constrains certain formula derivations. This distinction results in first-order logic having greater expressiveness for classical statements, whereas intuitionistic logic excels in contexts demanding constructive proofs but cannot express all classical truths.
Philosophical Implications and Foundations
Intuitionistic logic rejects the law of excluded middle, emphasizing constructive proof as a foundation for mathematical truth, contrasting with classical first-order logic's acceptance of non-constructive proofs. This philosophical shift foregrounds verification and computability, influencing foundational perspectives on mathematics and knowledge. Intuitionistic logic aligns with a Brouwerian view of mathematics as mental constructions, reshaping notions of truth and existence in formal systems.
Practical Examples and Use Cases
Intuitionistic logic underpins constructive mathematics and computer science applications such as type theory and program extraction, where proofs correspond directly to algorithms, ensuring verifiable computations. First-order logic dominates formal verification, database theory, and artificial intelligence for expressing and reasoning about relationships among objects with quantifiers and predicates. Practical use cases for intuitionistic logic include proof assistants like Coq and Agda, while first-order logic is prevalent in automated theorem proving and model checking tools like Z3 and Prover9.
Intuitionistic logic Infographic
 libterm.com
libterm.com