Modal logic explores the concepts of necessity and possibility, extending classical logic by incorporating modal operators such as "necessarily" and "possibly." This branch of logic has applications in computer science, philosophy, linguistics, and artificial intelligence, providing tools for reasoning about knowledge, belief, time, and obligation. Discover how modal logic can deepen your understanding of these complex ideas by reading the rest of the article.
Table of Comparison
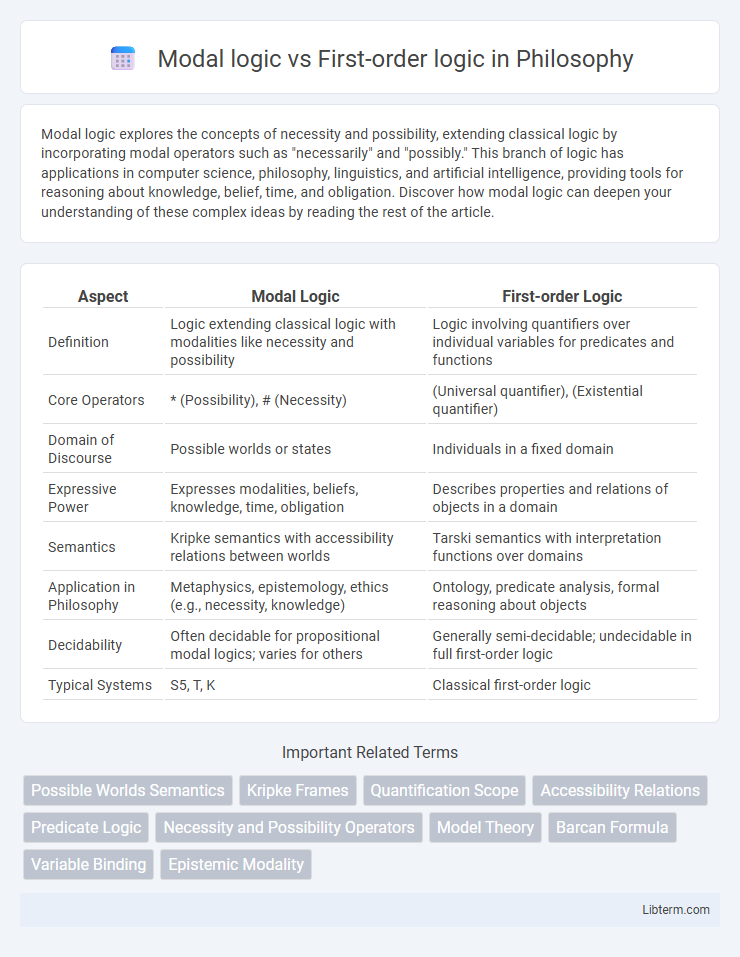
| Aspect | Modal Logic | First-order Logic |
|---|---|---|
| Definition | Logic extending classical logic with modalities like necessity and possibility | Logic involving quantifiers over individual variables for predicates and functions |
| Core Operators | * (Possibility), # (Necessity) | (Universal quantifier), (Existential quantifier) |
| Domain of Discourse | Possible worlds or states | Individuals in a fixed domain |
| Expressive Power | Expresses modalities, beliefs, knowledge, time, obligation | Describes properties and relations of objects in a domain |
| Semantics | Kripke semantics with accessibility relations between worlds | Tarski semantics with interpretation functions over domains |
| Application in Philosophy | Metaphysics, epistemology, ethics (e.g., necessity, knowledge) | Ontology, predicate analysis, formal reasoning about objects |
| Decidability | Often decidable for propositional modal logics; varies for others | Generally semi-decidable; undecidable in full first-order logic |
| Typical Systems | S5, T, K | Classical first-order logic |
Introduction to Modal Logic and First-Order Logic
Modal logic extends classical logic by incorporating modalities such as necessity and possibility, providing a framework to reason about various modes of truth beyond mere factual statements. First-order logic, in contrast, focuses on quantification over individuals and predicates, enabling precise formalization of statements about objects and their relationships within a domain. The introduction to modal logic emphasizes possible worlds semantics and accessibility relations, while first-order logic centers on quantifiers like (for all) and (there exists) to express propositions involving variable elements.
Foundations: Syntax and Semantics
Modal logic extends classical first-order logic by introducing modal operators such as * (possibly) and # (necessarily), enriching the syntax with these operators alongside standard quantifiers and connectives. Semantically, modal logic is grounded in possible world semantics, where truth values depend on accessibility relations between worlds, contrasting with first-order logic's interpretation over static domains and fixed variable assignments. This foundational difference allows modal logic to express nuanced modalities while first-order logic remains focused on quantification over individuals within a single domain.
Expressive Power Comparison
Modal logic excels in expressing concepts related to necessity, possibility, and temporal or epistemic modalities through modal operators, making it ideal for reasoning about knowledge, beliefs, and time. First-order logic offers greater expressive power by allowing quantification over individuals and relations, enabling detailed descriptions of objects and their interrelationships within a domain. While modal logic is more specialized and less expressive overall, first-order logic can encode modal reasoning by using relational structures, thus providing a broader framework for representing complex information.
Key Operators and Quantifiers
Modal logic employs key operators such as * (possibility) and # (necessity) to express modalities like possibility and necessity across possible worlds. First-order logic utilizes quantifiers (universal) and (existential) to handle statements about all or some elements within a domain. The fundamental distinction lies in modal logic's focus on states or worlds versus first-order logic's emphasis on individual elements and their properties.
Modeling Possibility and Necessity
Modal logic specializes in expressing concepts of possibility and necessity through modal operators, enabling nuanced modeling of statements that reflect potentiality and certainty. First-order logic primarily handles quantification over individuals and relations but cannot inherently capture modalities without extensions. The use of modal logic enhances formal systems by directly representing possible worlds semantics, making it indispensable for reasoning about knowledge, belief, and temporal modalities.
Applications in Computer Science and Philosophy
Modal logic enhances first-order logic by incorporating modalities like necessity and possibility, making it essential in computer science for verifying systems through model checking and reasoning about knowledge in artificial intelligence. In philosophy, modal logic provides tools for analyzing metaphysical concepts, such as possibility, necessity, and counterfactuals, addressing problems in epistemology and ontology. First-order logic remains foundational for formalizing mathematical theories and database query languages but lacks the expressive power to handle modal contexts inherent in many philosophical and computational scenarios.
Limitations and Decidability
Modal logic, emphasizing necessity and possibility, often struggles with expressiveness, limiting its ability to capture complex quantification found in first-order logic. First-order logic offers greater expressive power with quantifiers but faces undecidability in general, as many decision problems become algorithmically unsolvable. Modal logic's decidability varies by specific systems, typically enjoying better computational properties compared to the undecidable nature of full first-order logic.
Translating Between Modal and First-Order Logic
Translating between modal logic and first-order logic involves embedding modal operators like necessity (#) and possibility (*) into first-order structures using accessibility relations. In first-order logic, modal formulas are represented via relational predicates that correspond to possible world semantics, enabling rigorous interpretation and proof techniques. This translation preserves the expressiveness of modal statements within a classical logic framework, facilitating automated reasoning and model checking.
Common Use Cases and Examples
Modal logic excels in reasoning about necessity, possibility, and time, making it ideal for applications in computer science such as verifying system properties and modeling knowledge in artificial intelligence. First-order logic is widely used in mathematics, database theory, and formal verification due to its ability to express relations and quantify over individuals. For example, modal logic can model temporal sequences in program verification, while first-order logic is essential for expressing complex queries in relational databases.
Conclusion: Choosing the Right Logic System
Modal logic excels in expressing necessity and possibility, making it ideal for reasoning about knowledge, belief, and temporal events. First-order logic provides a robust framework for quantifying over individuals and expressing relations, suitable for precise mathematical and computational tasks. Selecting the right logic system depends on the specific requirements of expressiveness and domain relevance, with modal logic favored for modalities and first-order logic preferred for detailed structural analysis.
Modal logic Infographic
 libterm.com
libterm.com