The excluded middle principle states that for any proposition, either that proposition is true or its negation is true, with no middle ground. This fundamental law of classical logic underpins binary reasoning and decision-making processes, ensuring clarity and consistency in arguments. Explore the rest of the article to understand how this principle applies across various fields and why it is essential to your logical reasoning skills.
Table of Comparison
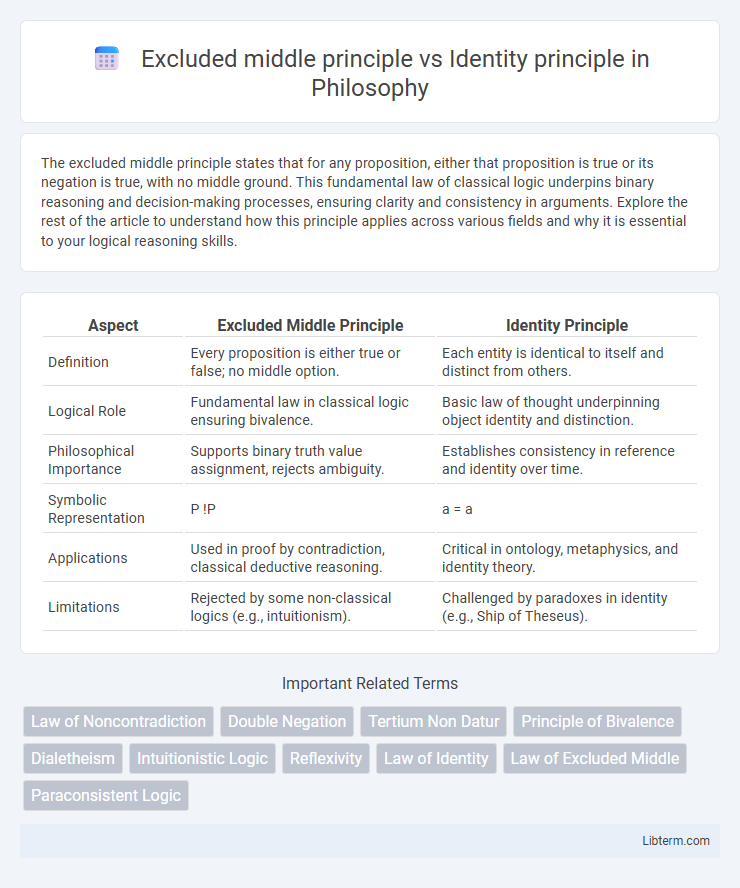
| Aspect | Excluded Middle Principle | Identity Principle |
|---|---|---|
| Definition | Every proposition is either true or false; no middle option. | Each entity is identical to itself and distinct from others. |
| Logical Role | Fundamental law in classical logic ensuring bivalence. | Basic law of thought underpinning object identity and distinction. |
| Philosophical Importance | Supports binary truth value assignment, rejects ambiguity. | Establishes consistency in reference and identity over time. |
| Symbolic Representation | P !P | a = a |
| Applications | Used in proof by contradiction, classical deductive reasoning. | Critical in ontology, metaphysics, and identity theory. |
| Limitations | Rejected by some non-classical logics (e.g., intuitionism). | Challenged by paradoxes in identity (e.g., Ship of Theseus). |
Understanding the Excluded Middle Principle
The Excluded Middle Principle asserts that for any proposition, either that proposition is true or its negation is true, emphasizing binary truth values without middle alternatives. It contrasts with the Identity Principle, which states that each thing is identical to itself, focusing on self-consistency rather than truth dichotomy. Understanding the Excluded Middle Principle is crucial in classical logic, where it underpins proof techniques like reductio ad absurdum by eliminating intermediate truth states.
Defining the Identity Principle
The Identity Principle asserts that each entity is identical to itself, establishing a foundational rule in classical logic that for any proposition A, A is A. This principle provides a clear criterion for object permanence and consistency in logical reasoning, distinguishing entities by their inherent properties. Understanding the Identity Principle clarifies how objects or concepts maintain their distinct identities despite changing conditions.
Historical Origins of Both Principles
The Excluded Middle Principle, tracing back to Aristotle's classical logic in the 4th century BCE, asserts that for any proposition, either it or its negation must be true, establishing a foundation for binary truth values. The Identity Principle, also rooted in Aristotelian logic, holds that every entity is identical to itself, serving as a fundamental axiom in classical metaphysics and formal reasoning. Both principles emerged from early Greek philosophical inquiries into the nature of truth and existence, influencing the development of Western logic and epistemology.
Core Differences Between Excluded Middle and Identity
The Excluded Middle principle asserts that for any proposition, either it or its negation must be true, emphasizing binary truth values without intermediate options. The Identity principle states that an entity is identical to itself, stressing self-consistency over logical dichotomy. Core differences lie in Excluded Middle addressing truth valuation of propositions, while Identity centers on the inherent sameness of an object or concept.
Philosophical Significance in Formal Logic
The Excluded Middle Principle asserts that for any proposition, either it is true or its negation is true, emphasizing binary truth values fundamental to classical logic. The Identity Principle, focused on self-sameness, states that every entity is identical to itself, serving as a core axiom ensuring consistency and clarity in logical expressions. Their philosophical significance lies in structuring formal logic by establishing foundational rules for truth evaluation and the coherence of entities within logical systems.
Applications in Mathematical Reasoning
The excluded middle principle asserts that every proposition is either true or false, which is essential for classical logic proofs and verification in mathematical reasoning. The identity principle, stating that each entity is identical to itself, underpins the consistent use of symbols and variables across equations and theorems. Both principles guide the formulation and validation of proofs, ensuring clarity and rigor in deductive mathematics.
Implications for Computer Science and Programming
The Excluded Middle principle asserts that every proposition is either true or false, which underpins classical logic frameworks used in algorithm design and decision-making processes in programming. The Identity principle emphasizes that an entity is identical to itself, supporting data consistency and object identity management in software development. Understanding these principles aids in optimizing logical reasoning engines, improving type systems, and enhancing compiler correctness in computer science.
Common Misconceptions Compared
The Excluded Middle Principle asserts that a statement is either true or false, rejecting any middle ground, while the Identity Principle states that each thing is identical to itself, emphasizing self-consistency. Common misconceptions confuse the Excluded Middle with strict binary logic and overlook contexts like fuzzy logic where truth values may vary. Misinterpretations of the Identity Principle often involve conflating it with equivalence relations, failing to recognize its foundational role in preserving object distinction in classical logic.
Influence on Modern Logic Systems
The Excluded Middle principle asserts that every proposition is either true or false, forming a basis for classical logic systems and enabling binary decision-making in computational frameworks. The Identity principle maintains that each entity is identical to itself, underpinning the coherence of logical expressions and consistency in reasoning processes. These principles critically influence modern logic systems by establishing foundational rules that support formal verification, automated theorem proving, and algorithmic logic design.
Summary: Contrasting Roles in Logical Theory
The Excluded Middle Principle asserts that for any proposition, either it or its negation must be true, establishing a binary framework essential for classical logic. In contrast, the Identity Principle maintains that each entity is identical to itself, grounding the concept of self-sameness and coherence in logical expressions. Together, these principles serve distinct yet complementary roles: the Excluded Middle enforces decisiveness in truth values, while the Identity Principle ensures consistency in referencing and reasoning about objects.
Excluded middle principle Infographic
 libterm.com
libterm.com