Bayesian inference is a statistical method that updates the probability of a hypothesis based on new evidence or data. It combines prior knowledge with observed information to make more accurate predictions and decisions. Discover how Bayesian inference can enhance your data analysis and improve model accuracy by reading the full article.
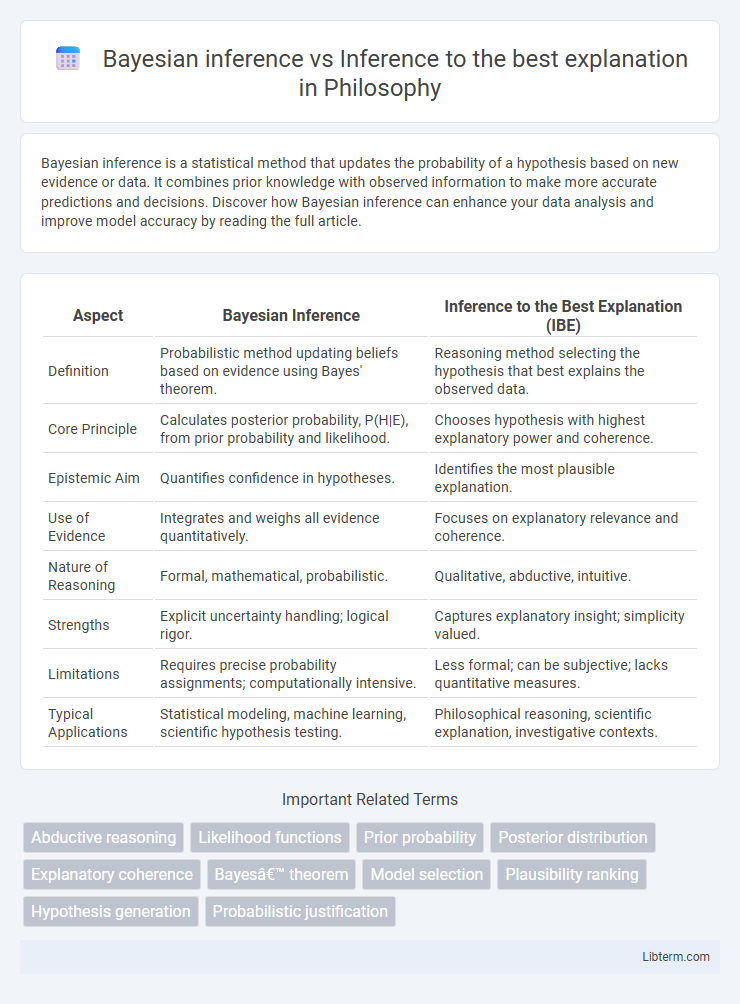
Table of Comparison
| Aspect | Bayesian Inference | Inference to the Best Explanation (IBE) |
|---|---|---|
| Definition | Probabilistic method updating beliefs based on evidence using Bayes' theorem. | Reasoning method selecting the hypothesis that best explains the observed data. |
| Core Principle | Calculates posterior probability, P(H|E), from prior probability and likelihood. | Chooses hypothesis with highest explanatory power and coherence. |
| Epistemic Aim | Quantifies confidence in hypotheses. | Identifies the most plausible explanation. |
| Use of Evidence | Integrates and weighs all evidence quantitatively. | Focuses on explanatory relevance and coherence. |
| Nature of Reasoning | Formal, mathematical, probabilistic. | Qualitative, abductive, intuitive. |
| Strengths | Explicit uncertainty handling; logical rigor. | Captures explanatory insight; simplicity valued. |
| Limitations | Requires precise probability assignments; computationally intensive. | Less formal; can be subjective; lacks quantitative measures. |
| Typical Applications | Statistical modeling, machine learning, scientific hypothesis testing. | Philosophical reasoning, scientific explanation, investigative contexts. |
Introduction to Bayesian Inference
Bayesian inference is a statistical method that updates the probability of a hypothesis based on new evidence by applying Bayes' theorem, integrating prior knowledge with observed data. It contrasts with Inference to the Best Explanation (IBE), which selects the hypothesis that most plausibly accounts for the evidence without formal probabilistic updating. Bayesian inference provides a mathematically rigorous framework for quantifying uncertainty and refining beliefs, making it essential in fields such as machine learning, statistics, and decision theory.
Overview of Inference to the Best Explanation (IBE)
Inference to the Best Explanation (IBE) is a method of reasoning that selects the hypothesis providing the most coherent and comprehensive account of observed data. IBE emphasizes explanatory virtues such as simplicity, scope, and plausibility to evaluate competing hypotheses. This approach contrasts with Bayesian inference by prioritizing the explanatory quality over probabilistic calculations.
Historical Context and Philosophical Foundations
Bayesian inference, rooted in Thomas Bayes' 18th-century work, formalizes probability updating based on evidence using Bayes' theorem. Inference to the best explanation, championed by philosophers like Charles Sanders Peirce and Gilbert Harman in the 20th century, emphasizes selecting hypotheses that provide the most coherent and plausible explanation. Bayesianism relies on mathematical probability axioms, while IBE is grounded in explanatory virtues such as simplicity and coherence within epistemology.
Key Principles of Bayesian Reasoning
Bayesian inference relies on updating the probability of a hypothesis based on prior knowledge and new evidence using Bayes' theorem, emphasizing a quantitative approach to uncertainty. It calculates posterior probabilities by combining prior probabilities with likelihoods derived from observed data, allowing for continuous refinement of beliefs. In contrast, inference to the best explanation selects hypotheses based on explanatory power without formal probability calculations, focusing on which explanation most plausibly accounts for the evidence.
Core Elements of IBE Methodology
Inference to the best explanation (IBE) emphasizes selecting the hypothesis that most plausibly accounts for the observed data based on criteria such as coherence, simplicity, and explanatory power. Its core elements include abductive reasoning, where explanatory hypotheses are evaluated contextually without strict probabilistic quantification. Bayesian inference, by contrast, relies on updating probabilities of hypotheses through Bayes' theorem, integrating prior beliefs with new evidence quantitatively, whereas IBE prioritizes qualitative assessment and explanatory virtues.
Bayesian vs IBE: Similarities and Differences
Bayesian inference and Inference to the Best Explanation (IBE) both aim to evaluate hypotheses but differ in methodology and emphasis. Bayesian inference uses probabilistic reasoning to update the likelihood of hypotheses based on evidence, quantifying uncertainty through prior and posterior probabilities. In contrast, IBE selects the hypothesis that best explains the available data, emphasizing explanatory power and coherence rather than formal probability measures.
Strengths and Limitations of Bayesian Inference
Bayesian inference excels in quantifying uncertainty by updating probabilities with new evidence, providing a rigorous mathematical framework for decision-making under uncertainty. Its strength lies in incorporating prior knowledge and delivering precise posterior probabilities, but it requires well-defined priors which can introduce subjective bias and computational complexity. Limitations of Bayesian inference include sensitivity to the choice of priors and challenges in managing large datasets or complex models without extensive computational resources.
Strengths and Limitations of IBE
Inference to the Best Explanation (IBE) excels in its ability to leverage explanatory power to guide hypothesis choice, making it highly intuitive for scientific reasoning where data is complex or incomplete. Its strength lies in prioritizing hypotheses that provide coherent and comprehensive narratives, but it lacks the formal probabilistic framework of Bayesian inference, which can lead to subjective judgments and biases. IBE's limitation is its vulnerability to competing explanations of equal plausibility without a clear metric, unlike Bayesian inference's quantitative likelihood assessments.
Real-World Applications: Case Studies and Examples
Bayesian inference is widely applied in medical diagnostics and machine learning, where probabilistic models update beliefs based on new evidence, such as in predicting disease outcomes or enhancing speech recognition. Inference to the best explanation (IBE) excels in forensic science and historical research by selecting hypotheses that most coherently account for observed facts, like reconstructing crime sequences or interpreting archaeological findings. Case studies in climate science demonstrate Bayesian methods quantifying uncertainty in model predictions, whereas IBE guides the formulation of theories that best explain complex environmental data patterns.
Conclusion: Choosing the Right Inference Approach
Selecting the appropriate inference method depends on the context of the problem and the nature of the data available. Bayesian inference provides a probabilistic framework ideal for updating beliefs with new evidence, especially when quantifying uncertainty is crucial. Inference to the best explanation excels in generating hypotheses that best account for observed phenomena, making it valuable when dealing with complex or incomplete data sets.
Bayesian inference Infographic
 libterm.com
libterm.com