The Law of Noncontradiction is a fundamental principle in classical logic stating that contradictory statements cannot both be true in the same sense at the same time. This rule underpins rational discourse and critical thinking by ensuring consistency and coherence in arguments and beliefs. Explore the rest of the article to deepen your understanding of how this law influences various fields of philosophy and reasoning.
Table of Comparison
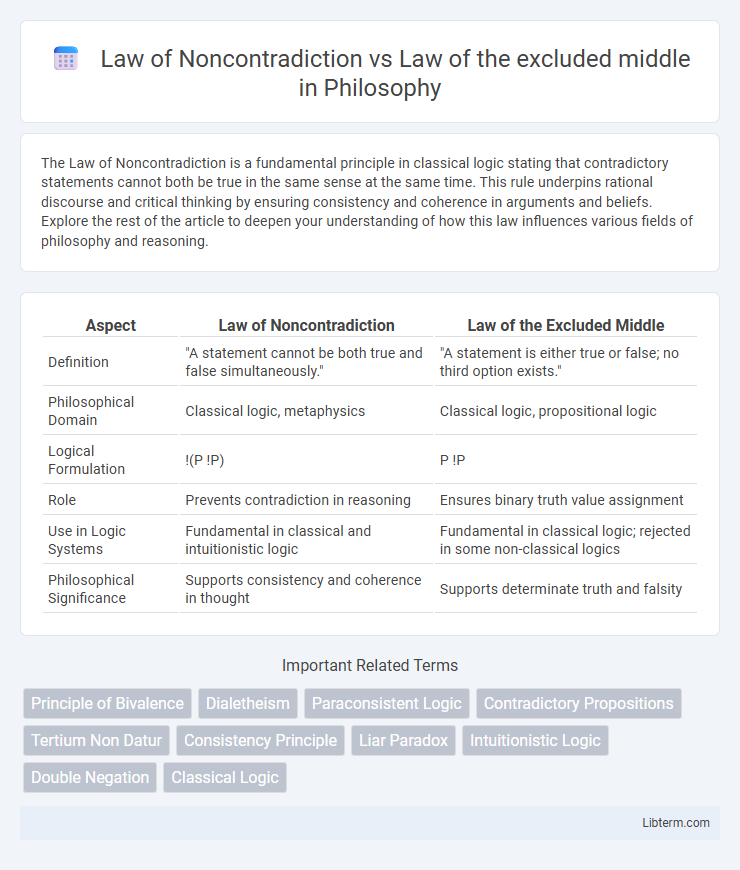
| Aspect | Law of Noncontradiction | Law of the Excluded Middle |
|---|---|---|
| Definition | "A statement cannot be both true and false simultaneously." | "A statement is either true or false; no third option exists." |
| Philosophical Domain | Classical logic, metaphysics | Classical logic, propositional logic |
| Logical Formulation | !(P !P) | P !P |
| Role | Prevents contradiction in reasoning | Ensures binary truth value assignment |
| Use in Logic Systems | Fundamental in classical and intuitionistic logic | Fundamental in classical logic; rejected in some non-classical logics |
| Philosophical Significance | Supports consistency and coherence in thought | Supports determinate truth and falsity |
Introduction to Classical Laws of Thought
The Law of Noncontradiction asserts that a proposition cannot be both true and false simultaneously, forming a fundamental principle in classical logic and reasoning. The Law of the Excluded Middle states that for any proposition, either it or its negation must be true, embodying a binary truth value system essential to classical law of thought. Together, these laws establish the foundational framework for classical logic, ensuring consistency and decisiveness in deductive reasoning processes.
Defining the Law of Noncontradiction
The Law of Noncontradiction asserts that a statement and its negation cannot both be true simultaneously, establishing a fundamental principle for classical logic. This principle ensures consistency by prohibiting contradictory properties from coexisting in the same subject at the same time. In contrast, the Law of the Excluded Middle states that any proposition must be either true or false, with no third option, emphasizing bivalence rather than contradiction avoidance.
Understanding the Law of the Excluded Middle
The Law of the Excluded Middle asserts that for any proposition, either that proposition is true or its negation is true, leaving no middle ground or third option. This principle is fundamental in classical logic, ensuring binary truth values and enabling definitive conclusions in logical proofs. Understanding this law highlights the stark contrast with the Law of Noncontradiction, which prohibits a statement from being both true and false simultaneously.
Historical Origins and Philosophical Foundations
The Law of Noncontradiction, tracing back to Aristotle's "Metaphysics," asserts that contradictory statements cannot both be true simultaneously, forming a foundational principle in classical logic and metaphysics. The Law of the Excluded Middle, also rooted in Aristotelian logic, states that for any proposition, either that proposition or its negation must be true, emphasizing binary truth values in classical reasoning. Both laws underpin Western philosophical traditions, with the former addressing the coherence of truth claims and the latter establishing the framework for definitive logical evaluation.
Core Differences Between the Two Laws
The Law of Noncontradiction states that a proposition cannot be both true and false simultaneously, emphasizing the impossibility of contradictory states coexisting. In contrast, the Law of the Excluded Middle asserts that for any proposition, either it is true or its negation is true, eliminating any middle or third option. The core difference lies in the Law of Noncontradiction forbidding simultaneous truth and falsity, while the Law of the Excluded Middle demands a binary truth value without intermediate possibilities.
Logical Implications and Applications
The Law of Noncontradiction asserts that a proposition cannot be both true and false simultaneously, ensuring consistency in logical reasoning and preventing paradoxes in formal systems. The Law of the Excluded Middle states that for any proposition, either it or its negation must be true, which underpins classical binary logic and enables definitive truth-value assignments in proofs and algorithmic reasoning. Logical implications of these laws influence computational logic, automated theorem proving, and the development of logical frameworks, while their applications extend to software verification, artificial intelligence, and mathematical logic.
Common Misconceptions and Clarifications
The Law of Noncontradiction states that a proposition cannot be both true and false simultaneously, while the Law of the Excluded Middle asserts that any proposition is either true or false, with no middle option. A common misconception is that these laws imply rigid binary thinking, but the Law of Noncontradiction only prohibits direct contradictions, and the Law of the Excluded Middle applies primarily in classical logic, not in intuitionistic or fuzzy logic frameworks. Clarifying these distinctions helps prevent misunderstandings in logical reasoning and highlights the nuanced application of these foundational principles in different logical systems.
Relevance in Modern Logic and Debate
The Law of Noncontradiction, asserting that contradictory statements cannot both be true in the same context, remains fundamental in classical logic, ensuring coherence and consistency in arguments and mathematical proofs. The Law of the Excluded Middle, positing that every proposition is either true or false with no middle ground, underpins binary decision-making but encounters challenges in intuitionistic and fuzzy logics, reflecting debates on truth values beyond absolutes. Modern logic and philosophical debate engage with both laws critically, exploring their limitations and applicability in areas such as quantum computing, where classical binary logic may not fully capture complex phenomena.
Challenges and Critiques from Non-Classical Logics
The Law of Noncontradiction, stating that contradictory propositions cannot both be true simultaneously, faces challenges in paraconsistent logics where contradictions are tolerable without entailing triviality. The Law of the Excluded Middle, asserting every proposition is either true or false, is critiqued by intuitionistic logic which denies this binary status by requiring constructive proof for truth claims. Non-classical logics like dialetheism further complicate these principles by allowing true contradictions and rejecting strict bivalence, prompting a reevaluation of classical logical foundations.
Conclusion: Harmonizing the Laws in Reasoning
The Law of Noncontradiction asserts that contradictory statements cannot both be true simultaneously, ensuring consistency in logical arguments, while the Law of the Excluded Middle dictates that any statement must be either true or false, eliminating ambiguity. Harmonizing these laws reinforces robust reasoning by establishing clear boundaries for truth values, preventing logical fallacies, and supporting definitive conclusions. This integration enhances formal logic systems by validating that propositions are either confirmed or denied without contradiction, crucial for effective problem-solving and decision-making processes.
Law of Noncontradiction Infographic
 libterm.com
libterm.com