Paraconsistent logic challenges traditional principles by allowing contradictions to coexist without collapsing into complete inconsistency, making it valuable for handling paradoxes in complex systems. This approach benefits fields like computer science, artificial intelligence, and philosophy by providing robust frameworks for reasoning in uncertain or conflicting information environments. Explore the rest of the article to understand how paraconsistent logic can enhance your critical thinking and problem-solving skills.
Table of Comparison
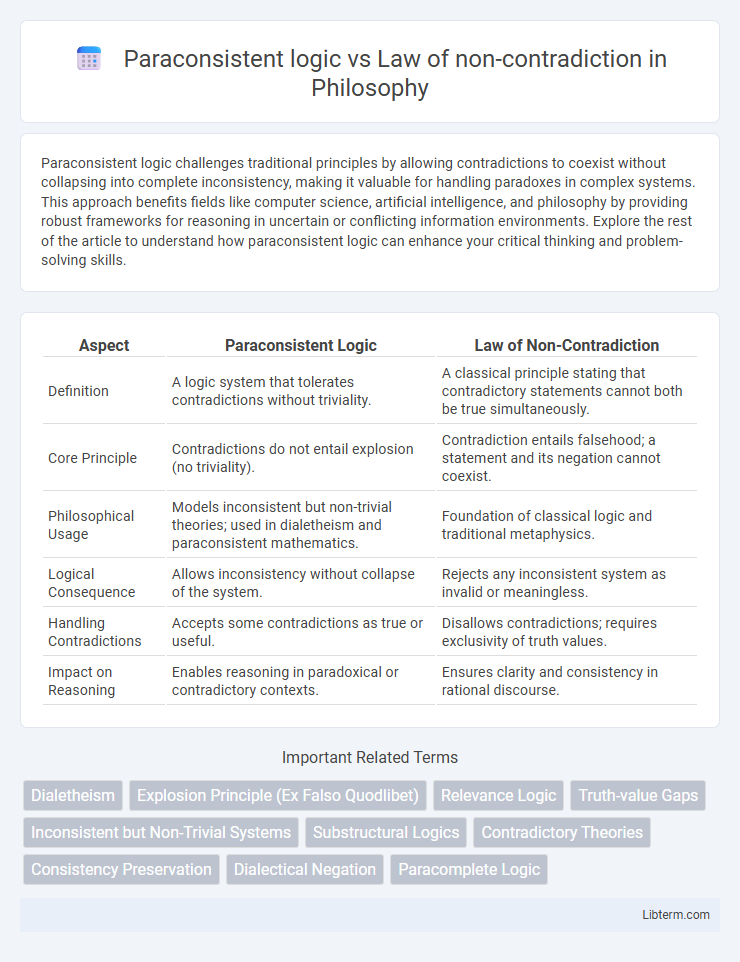
| Aspect | Paraconsistent Logic | Law of Non-Contradiction |
|---|---|---|
| Definition | A logic system that tolerates contradictions without triviality. | A classical principle stating that contradictory statements cannot both be true simultaneously. |
| Core Principle | Contradictions do not entail explosion (no triviality). | Contradiction entails falsehood; a statement and its negation cannot coexist. |
| Philosophical Usage | Models inconsistent but non-trivial theories; used in dialetheism and paraconsistent mathematics. | Foundation of classical logic and traditional metaphysics. |
| Logical Consequence | Allows inconsistency without collapse of the system. | Rejects any inconsistent system as invalid or meaningless. |
| Handling Contradictions | Accepts some contradictions as true or useful. | Disallows contradictions; requires exclusivity of truth values. |
| Impact on Reasoning | Enables reasoning in paradoxical or contradictory contexts. | Ensures clarity and consistency in rational discourse. |
Introduction to Paraconsistent Logic
Paraconsistent logic challenges the Law of Non-Contradiction by allowing contradictory statements to coexist without leading to triviality. It provides a formal framework where contradictions do not entail every proposition, enabling reasoning in contexts with inconsistent or incomplete information. This logic is crucial for applications in artificial intelligence, knowledge representation, and legal reasoning where classical binary logic falls short.
Understanding the Law of Non-Contradiction
The Law of Non-Contradiction states that contradictory statements cannot both be true simultaneously, serving as a fundamental principle in classical logic. Paraconsistent logic challenges this by allowing contradictions without collapsing into triviality, enabling reasoning in contexts where inconsistencies exist. Understanding the Law of Non-Contradiction highlights its role in maintaining logical coherence while paraconsistent logic expands the boundaries of classical reasoning frameworks.
Historical Development of Contradiction Handling
Paraconsistent logic emerged in the mid-20th century as a formal framework designed to handle contradictions without descending into trivialism, directly challenging the classical Law of Non-Contradiction established by Aristotle, which asserts that contradictory statements cannot both be true simultaneously. Historically, classical logic strictly upheld this law, limiting the capacity to manage inconsistent or incomplete information, whereas paraconsistent systems, initiated by logicians like Stanislaw Jaskowski and Newton da Costa, allow contradictions to coexist without collapsing deductive reasoning. This shift marked a significant evolution in philosophical logic and applications in fields such as computer science and knowledge representation, where inconsistent data is common but must be reasoned about effectively.
Key Principles of Paraconsistent Logic
Paraconsistent logic challenges the Law of Non-Contradiction by allowing contradictory statements to coexist without collapsing the system into triviality. It introduces key principles such as the rejection of explosion, meaning that from a contradiction, not every statement can be inferred, preserving meaningful reasoning in inconsistent information environments. This logic is essential in handling paradoxes, inconsistent databases, and real-world applications where classical logic's strict non-contradiction requirement fails.
Comparing Paraconsistent Logic and Classical Logic
Paraconsistent logic challenges the Law of Non-Contradiction by allowing contradictory statements to coexist without collapsing into triviality, unlike classical logic which strictly forbids contradictions. Classical logic maintains that a contradiction implies any statement can be true, whereas paraconsistent logic employs specialized inference rules to isolate contradictions and prevent explosion. This makes paraconsistent logic particularly useful in fields dealing with inconsistent or incomplete information, such as artificial intelligence and legal reasoning.
Philosophical Implications of Rejecting the Law of Non-Contradiction
Rejecting the Law of Non-Contradiction in paraconsistent logic challenges classical metaphysics by allowing contradictory statements to coexist without collapsing into triviality. This philosophical shift undermines traditional binary truth values, enabling the modeling of real-world scenarios marked by vagueness, paradox, and inconsistency. Embracing paraconsistent frameworks promotes a more nuanced epistemology where truth is not strictly dichotomous, expanding the scope of logical discourse and ontological inquiry.
Practical Applications of Paraconsistent Reasoning
Paraconsistent logic enables reasoning in the presence of contradictory information without descending into triviality, unlike classical logic which strictly adheres to the law of non-contradiction. Practical applications of paraconsistent reasoning include robust knowledge-based systems, fault-tolerant computing, and handling inconsistent data in artificial intelligence and databases. This approach allows systems to function effectively even when faced with conflicting inputs, improving decision-making and error management in complex environments.
Criticisms and Challenges Facing Paraconsistent Logic
Paraconsistent logic challenges the Law of Non-Contradiction by allowing contradictions without triviality, which faces criticism for undermining classical reasoning principles foundational to mathematics and philosophy. Critics argue that paraconsistent logic complicates proof theory and lacks intuitive clarity, making it difficult to reconcile with established logical frameworks. Furthermore, integrating paraconsistent systems into practical applications is challenging due to limited consensus on handling contradictions in computational and epistemic contexts.
Notable Theorists and Major Debates
Paraconsistent logic, pioneered by Newton da Costa and further developed by Graham Priest, challenges the universal applicability of the Law of Non-Contradiction, traditionally upheld by classical logicians such as Aristotle and Frege. Major debates center on whether contradictions must be strictly excluded from rational discourse, with paraconsistent theorists arguing for a logic system tolerating contradictions without collapse, while classical logicians defend the necessity of non-contradiction for coherent reasoning. This discourse profoundly impacts fields like philosophy, mathematics, and computer science, where handling inconsistent data without triviality is crucial.
Future Directions in Logic and Contradiction Research
Future research in paraconsistent logic concentrates on refining frameworks that tolerate contradictions without collapsing into triviality, challenging the classical law of non-contradiction. Innovations include the development of adaptive logical systems capable of operating in inconsistent information environments, enhancing applications in artificial intelligence and knowledge representation. Emphasis on integrating paraconsistent principles with computational models aims to unlock new paradigms for reasoning under uncertainty and contradictory data.
Paraconsistent logic Infographic
 libterm.com
libterm.com