Classical music embodies timeless harmonies and intricate compositions that have influenced countless genres. Its rich textures and disciplined structure offer a profound listening experience that can enhance your appreciation for musical artistry. Explore the rest of the article to uncover the enduring impact and beauty of classical music.
Table of Comparison
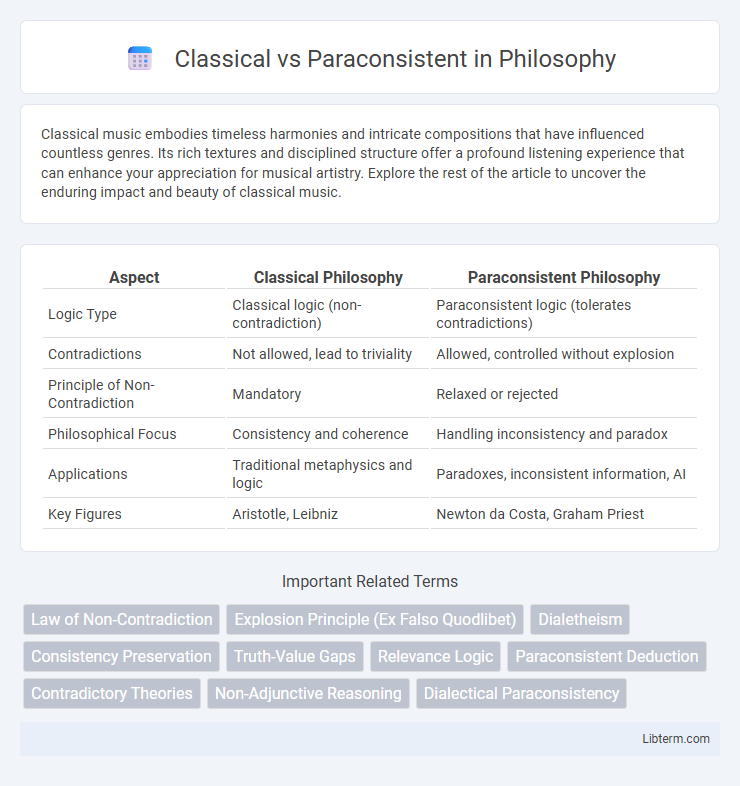
| Aspect | Classical Philosophy | Paraconsistent Philosophy |
|---|---|---|
| Logic Type | Classical logic (non-contradiction) | Paraconsistent logic (tolerates contradictions) |
| Contradictions | Not allowed, lead to triviality | Allowed, controlled without explosion |
| Principle of Non-Contradiction | Mandatory | Relaxed or rejected |
| Philosophical Focus | Consistency and coherence | Handling inconsistency and paradox |
| Applications | Traditional metaphysics and logic | Paradoxes, inconsistent information, AI |
| Key Figures | Aristotle, Leibniz | Newton da Costa, Graham Priest |
Introduction to Classical and Paraconsistent Logic
Classical logic operates on the principle of non-contradiction, where statements are either true or false, ensuring consistency but limiting the handling of contradictions. Paraconsistent logic relaxes this principle by allowing contradictions to coexist without leading to triviality, enabling reasoning in inconsistent but non-trivial systems. These logics provide foundational frameworks for varying approaches to truth, inference, and contradiction management in formal reasoning and computational applications.
Defining Classical Logic: Foundations and Principles
Classical logic is founded on principles such as the law of non-contradiction and the law of excluded middle, asserting that propositions are either true or false with no middle ground. It operates under bivalent semantics where every statement has a definitive truth value, and inference rules like modus ponens preserve truth across valid arguments. These foundational aspects enable classical logic to serve as the standard framework for mathematical reasoning and formal deduction.
Understanding Paraconsistent Logic: Key Concepts
Paraconsistent logic challenges classical logic by allowing contradictions to exist without collapsing into triviality, ensuring that contradictory statements do not entail every proposition. Key concepts include the rejection of the principle of explosion, which in classical logic states that from a contradiction, any statement can be derived. Paraconsistent frameworks are crucial for reasoning in inconsistent but non-trivial information systems, enabling more nuanced and flexible logical analysis.
Historical Evolution of Both Logics
Classical logic, originating from Aristotle's syllogistic framework and further formalized by Frege and Russell in the late 19th and early 20th centuries, establishes a bivalent system where every proposition is either true or false, underpinning most traditional mathematical and philosophical reasoning. Paraconsistent logic emerged in the mid-20th century as a response to inconsistencies in formal systems and real-world reasoning, pioneered by logicians like Jaskowski and da Costa to tolerate contradictions without collapsing into triviality. The historical evolution reflects a shift from rigid binary truth values in classical logic to more flexible systems in paraconsistent logic that accommodate contradiction and incomplete information.
Core Differences: Consistency and Contradiction
Classical logic strictly enforces the principle of consistency, where any contradiction implies every statement is true, known as the principle of explosion. Paraconsistent logic rejects this principle, allowing contradictions to coexist without collapsing into triviality, enabling reasoning in contexts with inconsistent information. This core divergence makes paraconsistent logic essential for handling paradoxes and real-world data where contradictions naturally arise.
Applications of Classical Logic
Classical logic underpins digital circuit design, formal verification, and database query languages due to its clear binary truth values ensuring precise computational outcomes. It is fundamental in mathematical theorem proving and artificial intelligence algorithms where deterministic reasoning is essential. Despite limitations in handling contradictions, classical logic remains the backbone of most programming languages and automated reasoning systems.
Applications of Paraconsistent Logic
Paraconsistent logic is widely applied in artificial intelligence for handling contradictory information without collapsing into triviality, making it essential in fault-tolerant systems and knowledge-based databases. In legal reasoning, paraconsistent logic allows for the modeling of conflicting laws or evidence, enabling more robust and realistic decision-making processes. Its use in medical diagnosis supports the integration of uncertain or contradictory symptoms, improving diagnostic accuracy and patient outcomes.
Advantages and Limitations of Classical Logic
Classical logic offers a well-established framework with clear rules for truth values, supporting consistent reasoning and definitive proof construction in mathematics and computer science. Its limitation lies in handling contradictions, as classical logic adheres to the principle of non-contradiction, causing any contradiction to lead to triviality, where any statement can be proved true. In contrast, paraconsistent logic is designed to manage contradictory information without collapse, making it advantageous in scenarios involving inconsistent or incomplete data.
Strengths and Challenges of Paraconsistent Logic
Paraconsistent logic excels in handling contradictory information without descending into triviality, making it crucial for applications in knowledge databases and AI systems where inconsistencies naturally occur. Its strength lies in allowing reasoning within inconsistent datasets while preserving meaningful conclusions, unlike classical logic which collapses under contradictions. Challenges include the complexity of developing intuitive proof systems and the limited standardization, which can hinder widespread adoption in practical computing environments.
Classical vs Paraconsistent Logic: Future Perspectives
Classical logic, founded on bivalent truth values and strict consistency, contrasts sharply with paraconsistent logic, which tolerates contradictions without triviality, enabling reasoning in inconsistent but non-trivial systems. Future perspectives emphasize integrating paraconsistent frameworks into artificial intelligence, database management, and knowledge representation to handle real-world data's inherent inconsistencies more robustly than classical frameworks. Enhanced computational models leveraging paraconsistent logic promise advances in error-resilient algorithms and flexible reasoning systems, driving innovation beyond the limitations of traditional classical logic.
Classical Infographic
 libterm.com
libterm.com