Likelihood measures the probability or chance that a specific event will occur based on available evidence and data. It plays a crucial role in statistics, decision-making, and risk assessment by helping you predict outcomes and make informed choices. Discover how understanding likelihood can enhance your analytical skills by reading the full article.
Table of Comparison
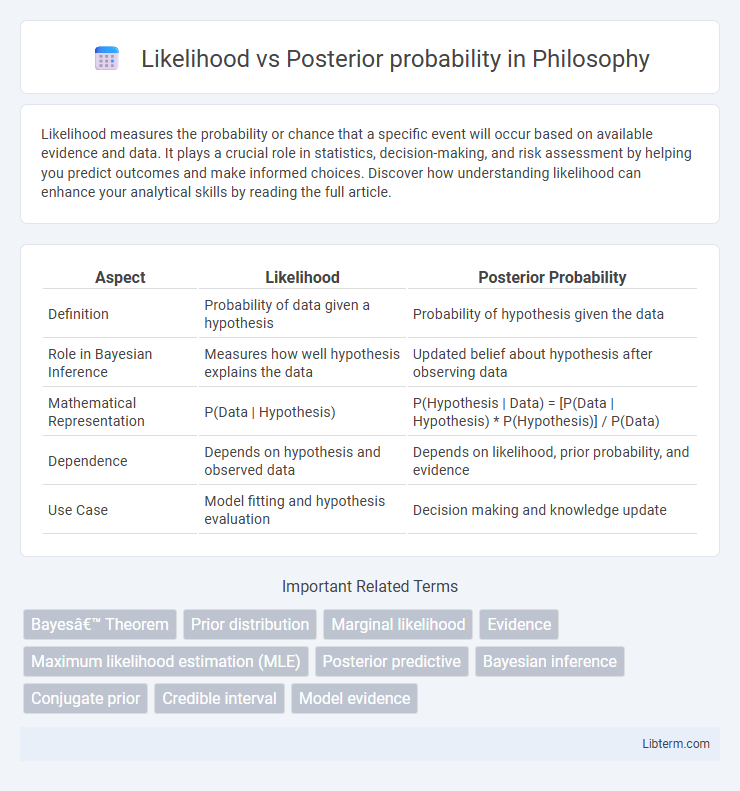
| Aspect | Likelihood | Posterior Probability |
|---|---|---|
| Definition | Probability of data given a hypothesis | Probability of hypothesis given the data |
| Role in Bayesian Inference | Measures how well hypothesis explains the data | Updated belief about hypothesis after observing data |
| Mathematical Representation | P(Data | Hypothesis) | P(Hypothesis | Data) = [P(Data | Hypothesis) * P(Hypothesis)] / P(Data) |
| Dependence | Depends on hypothesis and observed data | Depends on likelihood, prior probability, and evidence |
| Use Case | Model fitting and hypothesis evaluation | Decision making and knowledge update |
Understanding Likelihood and Posterior Probability
Likelihood measures the plausibility of observed data given specific parameter values, serving as a function in statistical inference. Posterior probability updates prior beliefs about parameters by incorporating observed data through Bayes' theorem, reflecting the probability of parameters given the data. Understanding the distinction helps in applying maximum likelihood estimation and Bayesian inference effectively for parameter estimation and decision-making.
Mathematical Definitions of Likelihood and Posterior
Likelihood is a fundamental concept in statistical inference, representing the probability of observed data given specific parameter values, mathematically expressed as L(th|x) = P(x|th). Posterior probability combines prior distribution and likelihood through Bayes' theorem, defined as P(th|x) = [P(x|th) * P(th)] / P(x), where P(th|x) denotes the updated belief about parameter th after observing data x. These definitions underpin parameter estimation in Bayesian statistics, distinguishing likelihood as a function of parameters for fixed data and posterior as a probability distribution of parameters given data.
The Role of Prior in Bayesian Inference
The likelihood function quantifies the probability of observed data given specific parameter values, while posterior probability updates these beliefs by combining the likelihood with prior knowledge through Bayes' theorem. The role of the prior in Bayesian inference is essential as it encodes existing information or assumptions about parameters before observing data, influencing the shape and location of the posterior distribution. Strong informative priors can significantly sway posterior estimates, especially in cases of limited data, whereas non-informative priors allow the likelihood to dominate the inference.
Likelihood Function: Concept and Applications
The Likelihood Function quantifies how probable observed data is given specific parameter values in a statistical model, serving as a foundational component in parameter estimation. It plays a crucial role in maximizing parameters to explain data patterns, especially in Maximum Likelihood Estimation (MLE). Applications span fields such as machine learning, bioinformatics, and signal processing, where assessing model fit to data guides decision-making and inference.
Posterior Probability: Meaning and Calculation
Posterior probability represents the updated probability of a hypothesis after observing new evidence, calculated using Bayes' theorem as the product of the likelihood and prior probability, normalized by the marginal likelihood. It quantifies the degree of belief in a hypothesis by integrating prior knowledge with observed data. This concept is fundamental in Bayesian inference, enabling dynamic updating of probabilities as more information becomes available.
Key Differences between Likelihood and Posterior
Likelihood measures the probability of observed data given specific parameter values, serving as a foundational concept in frequentist statistics. Posterior probability updates the belief about parameter values after observing data, combining prior information with the likelihood via Bayes' theorem. Key differences include that likelihood is not a probability distribution over parameters, whereas posterior probability is a true probability distribution reflecting updated uncertainty.
Illustrative Examples in Bayesian Statistics
In Bayesian statistics, the likelihood represents the probability of observing the data given a specific parameter value, such as the probability of flipping three heads in five coin tosses assuming a fair coin. Posterior probability updates this belief by combining the likelihood with a prior distribution, resulting in the probability of the parameter given the observed data, like revising the fairness of the coin after the tosses. For example, starting with a uniform prior on coin bias, the posterior after observing three heads out of five tosses is calculated using Bayes' theorem, showing how evidence refines parameter estimates.
Common Misconceptions about Likelihood vs Posterior
Likelihood measures the probability of observed data given a specific parameter value, whereas posterior probability updates the belief about the parameter after considering the observed data and prior information. A common misconception is treating likelihood as if it reflects the probability of the parameter itself, which it does not, since likelihood is not a probability distribution over parameters. Another frequent error is assuming posterior probability can be calculated without incorporating prior probabilities, ignoring the essential Bayes' theorem relationship that combines likelihood with priors.
Practical Implications in Data Analysis
Likelihood measures how well a statistical model explains observed data given fixed parameters, crucial for model fitting and parameter estimation techniques like maximum likelihood estimation (MLE). Posterior probability integrates prior knowledge with observed data through Bayes' theorem, providing updated parameter distributions essential for Bayesian inference and decision-making under uncertainty. Understanding the distinction shapes practical data analysis strategies, with likelihood optimizing model parameters from data alone, while posterior probability enables incorporating prior beliefs and quantifying parameter uncertainty.
Summary Table: Likelihood vs Posterior Probability
Likelihood measures the probability of observed data given specific model parameters, quantifying how well parameters explain the data, while posterior probability updates this likelihood by incorporating prior beliefs to reflect the probability of parameters given the observed data. In Bayesian inference, likelihood serves as the data-driven component, and posterior probability combines this with prior distributions to yield updated parameter estimates. This summary emphasizes likelihood as a data-focused measure and posterior probability as the integrative result reflecting updated knowledge after observing data.
Likelihood Infographic
 libterm.com
libterm.com