Actual infinities refer to completed, infinite quantities or collections that exist in reality, rather than just as abstract concepts. This idea challenges traditional notions of infinity, as it implies the existence of endless sets or magnitudes fully realized, influencing fields such as mathematics, cosmology, and philosophy. Explore the rest of this article to understand how actual infinities impact your perspective on the universe and beyond.
Table of Comparison
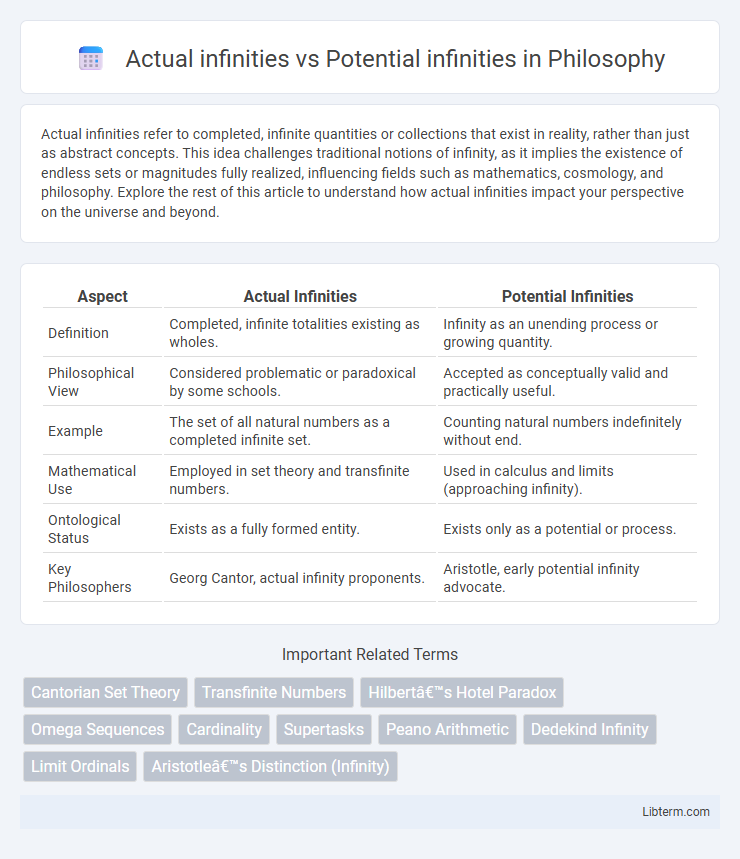
| Aspect | Actual Infinities | Potential Infinities |
|---|---|---|
| Definition | Completed, infinite totalities existing as wholes. | Infinity as an unending process or growing quantity. |
| Philosophical View | Considered problematic or paradoxical by some schools. | Accepted as conceptually valid and practically useful. |
| Example | The set of all natural numbers as a completed infinite set. | Counting natural numbers indefinitely without end. |
| Mathematical Use | Employed in set theory and transfinite numbers. | Used in calculus and limits (approaching infinity). |
| Ontological Status | Exists as a fully formed entity. | Exists only as a potential or process. |
| Key Philosophers | Georg Cantor, actual infinity proponents. | Aristotle, early potential infinity advocate. |
Introduction to Actual and Potential Infinities
Actual infinities refer to completed, infinite quantities existing as whole entities, such as the set of all natural numbers, whereas potential infinities describe processes that can continue indefinitely without ever reaching a final infinite total. The distinction originates from Aristotle's philosophy, where actual infinity implies an infinite magnitude present all at once, while potential infinity is an unending, never-completed progression. Understanding this difference is essential in set theory, calculus, and the philosophy of mathematics to clarify concepts of infinite sets and sequences.
Defining Actual Infinity
Actual infinity refers to a completed totality containing infinitely many elements simultaneously, often conceptualized as a set with an unbounded number of members. This contrasts with potential infinity, which denotes a process that grows without limit but never reaches an infinite quantity at any finite stage. In mathematics and philosophy, actual infinities underpin theories like set theory's infinite cardinalities, where infinite sets such as the set of natural numbers are treated as whole, completed entities.
Understanding Potential Infinity
Potential infinity refers to a process that can continue indefinitely without ever reaching a final infinite quantity, exemplified by the endless counting of natural numbers where numbers increase without bound but never form a completed infinite set. It contrasts with actual infinity, which considers infinity as a completed, unchanging totality, such as the set of all natural numbers viewed as an already complete entity. Understanding potential infinity involves recognizing it as a dynamic, never-fulfilled growth, essential in calculus and mathematical logic for concepts like limits and infinite sequences.
Historical Perspectives on Infinity
Throughout history, philosophers such as Aristotle distinguished actual infinities as completed, infinite totalities, while potential infinities were seen as processes that could grow without limit but never completed. Medieval scholars like Thomas Aquinas largely rejected actual infinity in physical reality, aligning with Aristotle's views, while early modern mathematicians began exploring potential infinity through limits and sequences. The 19th-century work of Georg Cantor revolutionized the understanding of infinity by rigorously defining actual infinities via set theory, introducing transfinite numbers that challenged prior historical perspectives.
Philosophical Arguments: Actual vs Potential Infinity
Philosophical debates on actual infinity versus potential infinity center on whether infinite quantities exist as completed entities or only as processes approaching infinity. Actual infinity posits that infinite sets or totals are fully formed and existent, a concept embraced in classical set theory but challenged for leading to paradoxes like Hilbert's hotel. Potential infinity views infinity as an endless progression without completion, aligning with Aristotelian thought and avoiding contradictions by treating infinity as a limit rather than a completed whole.
Mathematical Frameworks for Infinities
Actual infinities represent completed infinite totalities, such as the set of all natural numbers in set theory, while potential infinities denote processes that grow without bound but are never complete, exemplified in limits and sequences in calculus. Mathematical frameworks like Cantor's transfinite numbers rigorously define and manipulate actual infinities, establishing cardinalities and ordinals to classify different sizes of infinite sets. In contrast, foundational systems in analysis rely on potential infinity concepts through infinite sequences and series, emphasizing convergence and limiting behavior without asserting the existence of completed infinite entities.
Infinity in Set Theory: Cantor’s Contributions
Cantor's exploration of infinity in set theory distinguished between actual infinities, which are completed infinite sets, and potential infinities, representing never-ending processes. He introduced the concept of different sizes of infinite sets through cardinality, proving that the set of real numbers (continuum) is uncountably infinite and strictly larger than the countable infinity of natural numbers. Cantor's diagonal argument and the hierarchy of infinite cardinal numbers revolutionized mathematical understanding of infinite sets and their properties.
Real-World Implications of Infinite Concepts
Actual infinities represent completed infinite quantities, such as the set of all natural numbers, whereas potential infinities describe processes that can grow without bound, like counting indefinitely. In physics and cosmology, actual infinities challenge the understanding of space and time, suggesting paradoxes like infinite density in black holes, while potential infinities influence models of approximation and limits in real-world calculations. The distinction impacts theories in mathematics, cosmology, and computer science, shaping how infinite concepts are applied to solve practical problems and comprehend the universe's structure.
Criticisms and Limitations of Infinite Models
Actual infinities, representing completed infinite sets, face criticism for leading to paradoxes such as Hilbert's Hotel and violating intuitive notions of size and measure, challenging their applicability in physical reality. Potential infinities, viewed as never-ending processes, avoid these paradoxes but are limited in representing totalities, restricting their use in certain mathematical and physical models. Both infinite models encounter limitations in formal consistency and empirical validation, raising debates about their foundational roles in mathematics and physics.
Conclusion: Reconciling Actual and Potential Infinities
Reconciling actual and potential infinities requires understanding actual infinities as completed totalities, exemplified by the set of all natural numbers, whereas potential infinities represent endless processes or unbounded growth. Modern set theory and mathematical frameworks allow actual infinities to be handled rigorously, while calculus and analysis primarily utilize potential infinities to model limits and convergence. This dual approach harmonizes the conceptual and practical applications of infinity across mathematics and philosophy.
Actual infinities Infographic
 libterm.com
libterm.com