Intuitionistic logic is a framework that emphasizes constructive proof, rejecting the law of excluded middle and double negation elimination found in classical logic. It has profound applications in computer science, particularly in type theory and programming languages, where proof and computation intertwine. Discover how intuitionistic logic can transform your understanding of mathematical reasoning in the full article.
Table of Comparison
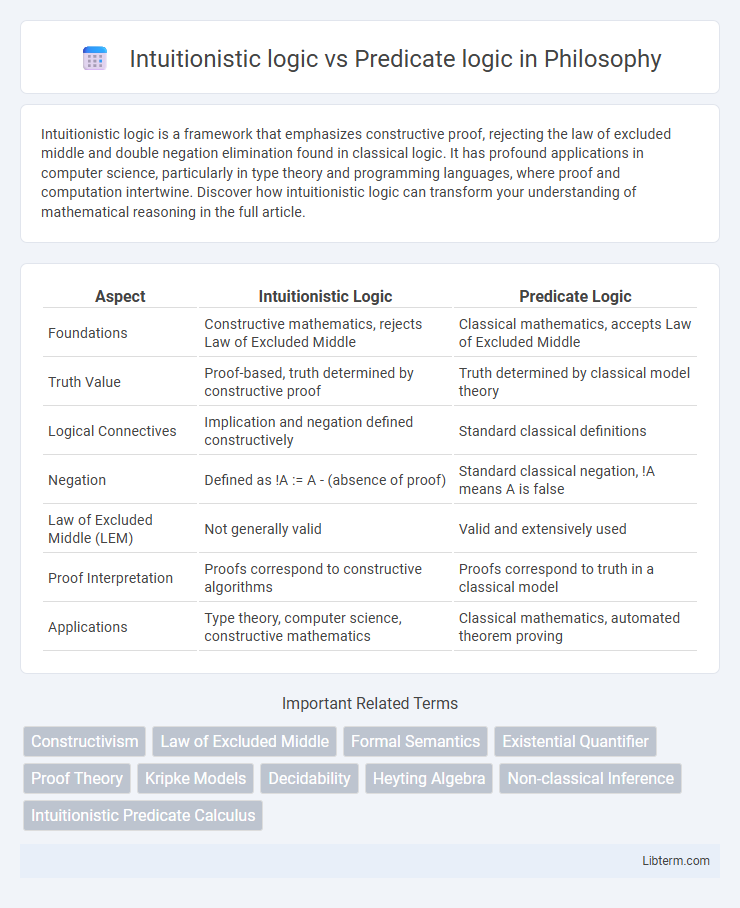
| Aspect | Intuitionistic Logic | Predicate Logic |
|---|---|---|
| Foundations | Constructive mathematics, rejects Law of Excluded Middle | Classical mathematics, accepts Law of Excluded Middle |
| Truth Value | Proof-based, truth determined by constructive proof | Truth determined by classical model theory |
| Logical Connectives | Implication and negation defined constructively | Standard classical definitions |
| Negation | Defined as !A := A - (absence of proof) | Standard classical negation, !A means A is false |
| Law of Excluded Middle (LEM) | Not generally valid | Valid and extensively used |
| Proof Interpretation | Proofs correspond to constructive algorithms | Proofs correspond to truth in a classical model |
| Applications | Type theory, computer science, constructive mathematics | Classical mathematics, automated theorem proving |
Introduction to Intuitionistic and Predicate Logic
Intuitionistic logic emphasizes constructivist proof principles, rejecting the law of excluded middle and double negation elimination, unlike classical predicate logic, which assumes these principles universally. Predicate logic extends propositional logic by incorporating quantifiers and variables to express statements about objects within a domain, forming the foundation of formal reasoning in mathematics and computer science. Intuitionistic predicate logic adapts these quantifiers under constructive interpretation, impacting proof methods and the semantics of logical formulas.
Historical Development and Philosophical Roots
Intuitionistic logic originated in the early 20th century through the work of L.E.J. Brouwer, emphasizing constructive proof and rejecting the law of excluded middle, contrasting with classical predicate logic developed by Frege and Peano, which allowed non-constructive reasoning. This shift was rooted in Brouwer's philosophical stance on mathematics as mental constructions rather than abstract entities, influencing the development of intuitionism as a foundational framework. Predicate logic formalized classical logic's universal and existential quantifiers, while intuitionistic logic modified these operations to align with its constructive interpretation, marking a fundamental philosophical divergence.
Formal Syntax: Structures and Symbols
Intuitionistic logic employs a formal syntax similar to predicate logic but restricts classical principles like the law of excluded middle, emphasizing constructivist interpretations of symbols. Both logics use quantifiers (, ), logical connectives (, , -, !), and variables, yet intuitionistic logic's proof system requires evidence for assertions rather than truth values. The syntactic structures in intuitionistic predicate logic maintain standard formation rules but differ semantically in proof interpretation, impacting inference rules and validation processes.
Semantics: Meaning and Interpretation
Intuitionistic logic's semantics emphasize constructive proofs, interpreting truth as the existence of explicit evidence rather than classical truth values, often formalized through Kripke models or Heyting algebras. Predicate logic relies on classical Tarski semantics, assigning fixed truth values to predicates over a domain, assuming the law of excluded middle and bivalence. This fundamental semantic difference shapes how meaning and interpretation function in each logic system, with intuitionistic logic rejecting non-constructive existence proofs that predicate logic accepts.
The Law of Excluded Middle: Acceptance and Rejection
Intuitionistic logic rejects the Law of Excluded Middle, which states that for any proposition P, either P is true or its negation !P is true, emphasizing constructive proof over classical binary truth values. Predicate logic, grounded in classical logic, accepts the Law of Excluded Middle as a fundamental principle, allowing proofs by contradiction and non-constructive arguments. This divergence impacts proof techniques and the interpretation of truth in formal systems, with intuitionistic logic requiring explicit evidence for assertions rather than relying on excluded middle's binary assumption.
Quantifiers in Intuitionistic vs. Predicate Logic
In intuitionistic logic, quantifiers are interpreted constructively, requiring explicit evidence for existential claims and a function-based approach to universals, contrasting with classical predicate logic's reliance on truth values independent of proof. The existential quantifier () in intuitionistic logic demands a witness, ensuring the constructibility of an element satisfying the property, while classical predicate logic allows for truth without such constructive evidence. Universally quantified statements () in intuitionistic logic require a method to transform any given instance into a proof, emphasizing computational content absent in classical predicate logic.
Constructive Proofs vs. Classical Proofs
Intuitionistic logic emphasizes constructive proofs, requiring explicit witness construction for existential claims, contrasting with predicate logic's classical proofs that accept non-constructive methods like the law of excluded middle. Constructive proofs in intuitionistic logic ensure verifiable computational content, making them foundational in areas like type theory and programming semantics. Classical predicate logic allows reasoning with proof by contradiction and omitted constructive detail, broadening theorem applicability but sacrificing guaranteed explicit constructions.
Applications in Mathematics and Computer Science
Intuitionistic logic underpins constructive mathematics by emphasizing proof existence, making it vital for type theory and formal verification in computer science. Predicate logic, with its classical truth-values framework, drives automated theorem proving and knowledge representation essential in artificial intelligence and database query languages. Both logics complement each other in bridging rigorous mathematical proof systems with practical computational algorithms.
Advantages and Limitations of Each Logic System
Intuitionistic logic offers advantages in constructive mathematics by emphasizing proof existence and avoiding the law of excluded middle, making it suitable for computer science applications like type theory and program verification. Predicate logic excels in expressiveness and classical reasoning, allowing robust handling of quantifiers and offering wide applicability in formal semantics and automated theorem proving. However, intuitionistic logic's rejection of classical principles can limit its expressiveness and complicate certain proofs, while predicate logic's reliance on classical truth values may not align with constructive or computational interpretations.
Conclusion: Choosing Between Intuitionistic and Predicate Logic
Choosing between intuitionistic logic and predicate logic depends on the nature of the reasoning task and philosophical stance; intuitionistic logic emphasizes constructivist principles, rejecting the law of excluded middle and requiring constructive proofs, making it suitable for computational interpretations and proof verification. Predicate logic, grounded in classical logic, accepts non-constructive proofs and is widely used in mathematics and formal semantics for expressing generality and quantification without constructivist constraints. The decision hinges on whether one prioritizes constructive validity and algorithmic interpretability (intuitionistic) or broader expressive power with classical interpretation (predicate logic).
Intuitionistic logic Infographic
 libterm.com
libterm.com