Propositional logic is the branch of logic that deals with propositions and their relationships through logical connectives such as AND, OR, and NOT. It forms the foundation for Boolean algebra and is essential for understanding logical reasoning in mathematics and computer science. Explore the rest of the article to deepen your understanding of propositional logic and its practical applications.
Table of Comparison
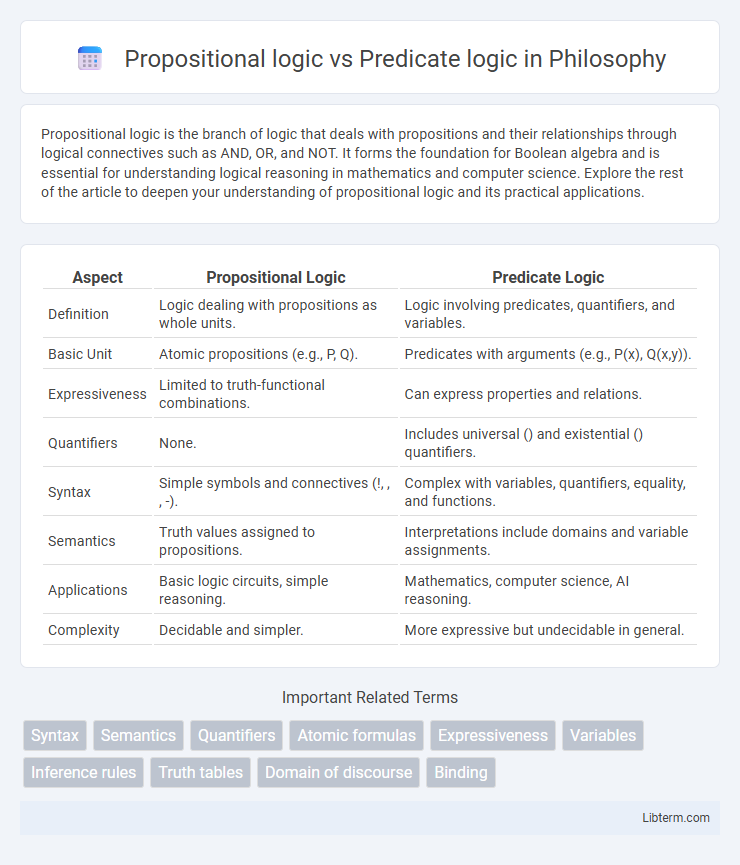
| Aspect | Propositional Logic | Predicate Logic |
|---|---|---|
| Definition | Logic dealing with propositions as whole units. | Logic involving predicates, quantifiers, and variables. |
| Basic Unit | Atomic propositions (e.g., P, Q). | Predicates with arguments (e.g., P(x), Q(x,y)). |
| Expressiveness | Limited to truth-functional combinations. | Can express properties and relations. |
| Quantifiers | None. | Includes universal () and existential () quantifiers. |
| Syntax | Simple symbols and connectives (!, , , -). | Complex with variables, quantifiers, equality, and functions. |
| Semantics | Truth values assigned to propositions. | Interpretations include domains and variable assignments. |
| Applications | Basic logic circuits, simple reasoning. | Mathematics, computer science, AI reasoning. |
| Complexity | Decidable and simpler. | More expressive but undecidable in general. |
Introduction to Propositional and Predicate Logic
Propositional logic analyzes statements as whole units using variables that represent simple propositions, focusing on their truth values and logical connectives such as AND, OR, and NOT. Predicate logic extends propositional logic by incorporating quantifiers and predicates that express properties of objects and relationships between them, enabling more detailed and structured representations of statements. This foundational difference makes predicate logic more expressive for formal reasoning, especially in mathematics, computer science, and linguistics.
Overview of Propositional Logic
Propositional logic, also known as sentential logic, deals with propositions that are either true or false and uses logical connectives such as AND, OR, NOT, and IMPLIES to form complex statements. It lacks the ability to express relationships between objects or quantify over them, which distinguishes it from predicate logic that introduces predicates and quantifiers like "for all" and "there exists." Propositional logic serves as the foundation for classical logic systems and is primarily used in fields like computer science, mathematics, and digital circuit design for reasoning about truth-functional statements.
Fundamentals of Predicate Logic
Predicate logic extends propositional logic by incorporating quantifiers and predicates, allowing statements about objects and their properties rather than merely whole propositions. It introduces variables, predicates, and quantifiers such as "forall" () and "exists" (), enabling the expression of more complex and precise logical relationships. The fundamentals of predicate logic include understanding syntax (terms, formulas), semantics (interpretations, models), and inference rules that facilitate reasoning about individual elements within a domain.
Syntax Differences
Propositional logic consists of simple, indivisible propositions represented by variables and logical connectives without internal structure analysis. Predicate logic extends propositional logic by including quantifiers, variables, predicates, and terms, enabling expressions about objects and their properties within a domain. Syntax in predicate logic incorporates function symbols, constants, and variables, allowing more complex statements than the flat, variable-only syntax of propositional logic.
Semantic Distinctions
Propositional logic deals with simple, declarative statements whose truth values are fixed, lacking internal structure to express relationships between objects. Predicate logic enhances expressiveness by incorporating quantifiers and predicates, allowing detailed representation of properties, relations, and object variables within a domain. The semantic distinction lies in predicate logic's ability to evaluate statements over individual elements, while propositional logic evaluates entire statements as atomic units without internal semantic content.
Expressive Power Comparison
Propositional logic represents statements as whole units with limited expressive power, unable to capture the internal structure of statements or quantify over elements. Predicate logic enhances expressive capacity by incorporating quantifiers and predicates, allowing detailed representation of relationships and properties within a domain. This increased expressiveness enables predicate logic to model complex reasoning tasks, such as those involving variables and quantification, which are beyond the scope of propositional logic.
Common Use Cases
Propositional logic is commonly used in digital circuit design, software testing, and simple decision-making systems where statements are clear and discrete without internal structure. Predicate logic is essential for knowledge representation in artificial intelligence, natural language processing, and database query systems, enabling reasoning about objects and their properties with quantifiers. While propositional logic handles straightforward true/false evaluations, predicate logic allows for more expressive modeling of real-world scenarios involving relationships and variables.
Advantages and Limitations
Propositional logic offers simplicity and ease of implementation, making it suitable for problems involving true or false statements without internal structure, but it lacks the expressive power to handle relationships or quantify variables. Predicate logic provides greater expressive capabilities by incorporating quantifiers and predicates, enabling detailed representation of objects and their properties, yet it is computationally more complex and often undecidable in general cases. The choice between propositional and predicate logic depends on the required level of expressiveness versus computational tractability in applications such as automated theorem proving and knowledge representation.
Practical Applications
Propositional logic is widely used in digital circuit design and simple automated reasoning tasks where statements are either true or false without internal structure. Predicate logic extends these capabilities by handling variables and quantifiers, making it essential for knowledge representation, database query languages, and artificial intelligence for expressing more complex relationships. Automated theorem proving and formal verification systems heavily rely on predicate logic to model real-world scenarios with precision and flexibility.
Conclusion and Key Takeaways
Propositional logic deals with simple, declarative statements and their truth values, making it suitable for basic logical operations but limited in expressing detailed relationships. Predicate logic extends propositional logic by incorporating quantifiers and predicates, enabling more precise representation of objects and their properties in complex reasoning. Key takeaway: predicate logic offers greater expressiveness and is essential for formalizing arguments involving variables and quantifiers, where propositional logic falls short.
Propositional logic Infographic
 libterm.com
libterm.com