Weak implication in logic describes a relationship where one statement suggests another with minimal certainty, often allowing the latter to be false even if the former is true. This concept contrasts with strong implication, which guarantees the truth of the consequent whenever the antecedent holds. Explore the full article to understand how weak implication influences reasoning and decision-making processes.
Table of Comparison
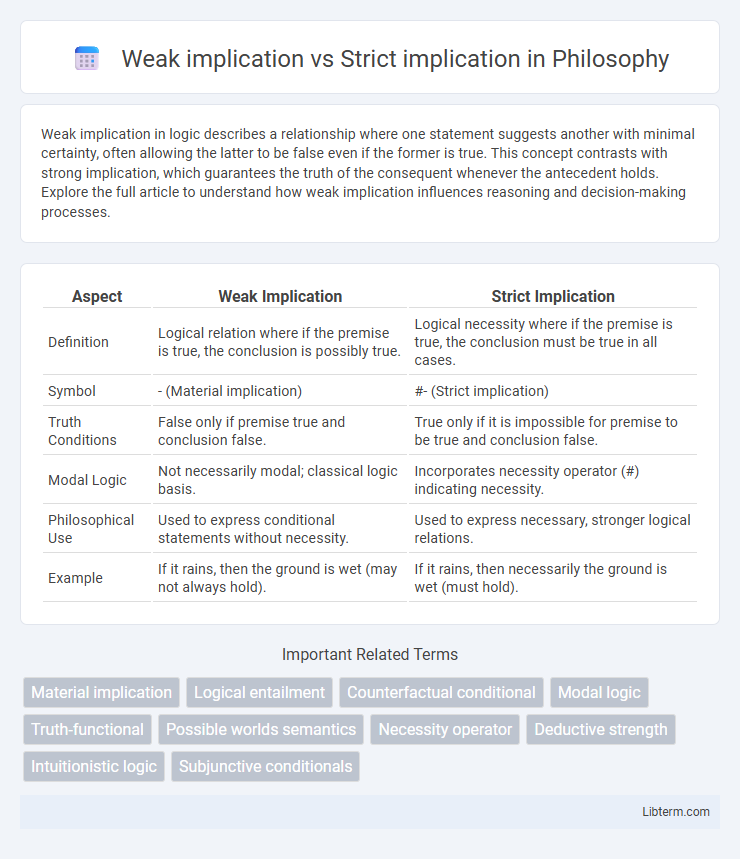
| Aspect | Weak Implication | Strict Implication |
|---|---|---|
| Definition | Logical relation where if the premise is true, the conclusion is possibly true. | Logical necessity where if the premise is true, the conclusion must be true in all cases. |
| Symbol | - (Material implication) | #- (Strict implication) |
| Truth Conditions | False only if premise true and conclusion false. | True only if it is impossible for premise to be true and conclusion false. |
| Modal Logic | Not necessarily modal; classical logic basis. | Incorporates necessity operator (#) indicating necessity. |
| Philosophical Use | Used to express conditional statements without necessity. | Used to express necessary, stronger logical relations. |
| Example | If it rains, then the ground is wet (may not always hold). | If it rains, then necessarily the ground is wet (must hold). |
Introduction to Logical Implication
Logical implication distinguishes between weak implication, where the truth of the antecedent does not guarantee the truth of the consequent but disallows the antecedent being true while the consequent is false, and strict implication, which requires that it is necessary for the consequent to be true whenever the antecedent is true across all possible worlds. Weak implication corresponds to material implication in classical logic, expressed as "if P then Q," and is false only when P is true and Q is false. Strict implication involves modal logic, embedding necessity, and is represented as "it is necessarily the case that if P then Q," emphasizing a stronger, more rigid logical connection.
Defining Weak Implication
Weak implication, in formal logic, refers to a conditional relationship where the truth of the antecedent does not guarantee the truth of the consequent but allows for it to be possibly true. It is defined by the semantic condition that if the antecedent is true, the consequent need not be true; however, if the antecedent is false, the implication is always true. Weak implication differs from strict implication, which demands a necessary connection ensuring the consequent must be true whenever the antecedent is true, reflecting a stronger modal or inferential relation.
Understanding Strict Implication
Strict implication in logic demands that if the antecedent is true, then the consequent must necessarily be true in all possible models, reflecting a stronger relationship than weak implication. Unlike weak implication, which allows for truth preservation under classical conditions, strict implication enforces a modal necessity, often represented in modal logic frameworks like S4 or S5. This ensures that strict implication captures necessity and not just truth-functional dependency, making it essential for formal systems requiring rigorous entailment criteria.
Key Differences Between Weak and Strict Implication
Weak implication in logic refers to a relationship where the truth of one statement suggests, but does not guarantee, the truth of another, while strict implication requires that if the first statement is true, the second must necessarily be true. Weak implication allows for cases where the antecedent may be false without affecting the implication, whereas strict implication aligns more closely with a necessity operator, emphasizing a stronger conditional connection. Key differences include the modal strength, with strict implication embodying necessity and weak implication embodying material or classical implication, and their use in different logical systems, such as modal logic for strict implication versus propositional logic for weak implication.
Formal Notation and Symbols
Weak implication, often denoted as \( \Rightarrow \), signifies a logical connective where if the antecedent is true, the consequent must be true, but it does not assert necessity beyond truth preservation. Strict implication, symbolized as \( \Box (p \rightarrow q) \) in modal logic, emphasizes necessity by asserting that in all possible worlds where \( p \) holds, \( q \) also holds, embedding a modal operator \( \Box \) that represents necessity. The formal distinction lies in weak implication's material conditional \( p \rightarrow q \) compared to strict implication's modalized form \( \Box (p \rightarrow q) \), which captures stronger semantic conditions beyond mere truth-functional evaluation.
Common Use Cases in Logic
Weak implication is often used in classical logic for statements where truth preservation is necessary but not guaranteed under all interpretations, such as in conditional proofs and hypothetical reasoning. Strict implication, common in modal logic, requires necessity of truth transfer between propositions, making it suitable for formal verification, knowledge representation, and reasoning about necessity and possibility. These distinctions guide applications in automated theorem proving and semantic analysis, where weak implication handles general inference and strict implication ensures stronger logical validity.
Examples Illustrating Each Implication
Weak implication can be illustrated by the statement "If it rains, the ground gets wet," where rain often causes wet ground but not necessarily in all cases due to other factors. Strict implication is exemplified by mathematical logic, such as "If a number is divisible by 4, then it is divisible by 2," which holds true in every instance without exception. These examples highlight that weak implication allows for exceptions or probable outcomes, while strict implication demands absolute certainty in the relationship.
Advantages and Limitations
Weak implication allows for more flexible logical inference by permitting conclusions based on partial or probabilistic evidence, making it useful in uncertain or approximate reasoning contexts. Strict implication, grounded in formal logic, ensures precise and unequivocal conclusions, which is advantageous for rigorous proof systems but can be overly restrictive for real-world scenarios. The main limitation of weak implication lies in its potential for ambiguity and lack of guarantee in truth preservation, whereas strict implication's rigidity often leads to difficulties in capturing nuanced or incomplete information.
Application in Mathematical Reasoning
Weak implication in mathematical reasoning allows for conclusions to hold under broader conditions, often used in proofs involving necessary but not sufficient conditions. Strict implication requires stronger, bidirectional logical equivalence, making it essential in establishing precise theorems and formal system axioms. Applications in formal logic, type theory, and automated theorem proving leverage strict implication to ensure rigorous deductive steps, while weak implication supports more flexible hypothesis testing and inference generation.
Conclusion and Summary
Weak implication allows conclusions that hold in some but not all interpretations, making it less definitive in logical reasoning. Strict implication requires that the conclusion follow necessarily from the premise across all possible worlds, ensuring stronger logical certainty. Understanding the distinction is crucial for applying appropriate inference rules in formal logic and computational reasoning.
Weak implication Infographic
 libterm.com
libterm.com