Linear algorithms process input data in a sequential manner, making them efficient for solving problems with a straightforward, step-by-step approach. Their simplicity ensures predictable performance, ideal for tasks where speed and clarity are essential. Explore the rest of the article to understand how linear methods can enhance your computational strategies.
Table of Comparison
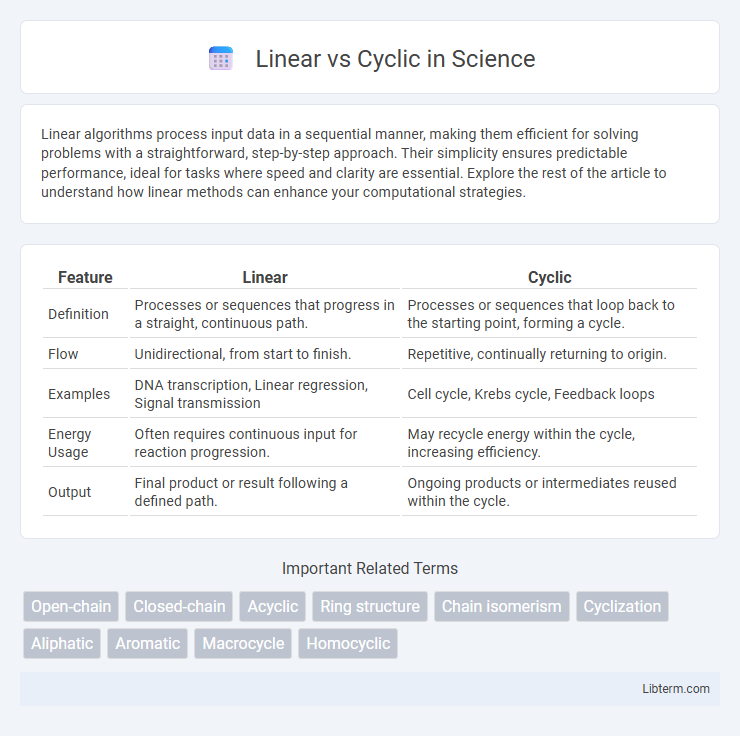
| Feature | Linear | Cyclic |
|---|---|---|
| Definition | Processes or sequences that progress in a straight, continuous path. | Processes or sequences that loop back to the starting point, forming a cycle. |
| Flow | Unidirectional, from start to finish. | Repetitive, continually returning to origin. |
| Examples | DNA transcription, Linear regression, Signal transmission | Cell cycle, Krebs cycle, Feedback loops |
| Energy Usage | Often requires continuous input for reaction progression. | May recycle energy within the cycle, increasing efficiency. |
| Output | Final product or result following a defined path. | Ongoing products or intermediates reused within the cycle. |
Introduction to Linear and Cyclic Structures
Linear structures organize elements sequentially in a straight line, facilitating straightforward access and traversal, such as arrays and linked lists. Cyclic structures form closed loops where the last element connects back to the first, enabling continuous iteration without a defined beginning or end, examples include circular linked lists and cyclic graphs. Understanding the distinction between linear and cyclic structures is essential for optimizing data storage and algorithm efficiency in computer science.
Fundamental Differences Between Linear and Cyclic Forms
Linear forms represent structures or processes arranged sequentially in a straight, unidirectional path, emphasizing a clear beginning and end, such as in linear equations or linear workflows. Cyclic forms, in contrast, are characterized by repetition and recurrence, forming closed loops where the end connects back to the beginning, exemplified by cyclic processes like the Krebs cycle or cyclic redundancy checks. The fundamental difference lies in linear forms progressing in one direction without repetition, while cyclic forms continuously loop, enabling ongoing repetition and regeneration.
Chemical Properties: Linear vs Cyclic Compounds
Linear compounds typically exhibit higher reactivity due to the presence of accessible terminal functional groups and less steric hindrance, which facilitates chemical interactions. Cyclic compounds often possess enhanced stability from ring strain and conjugation effects, influencing their electron distribution and reaction pathways. The distinct spatial arrangements in linear and cyclic structures significantly impact their chemical properties such as acidity, basicity, and reactivity toward nucleophiles and electrophiles.
Structural Stability: Linear Versus Cyclic Molecules
Linear molecules generally exhibit lower structural stability compared to cyclic molecules due to the absence of ring strain and enhanced orbital overlap found in cyclic structures. Cyclic molecules benefit from ring tension and conjugation effects, which contribute to increased rigidity and stability. The stability of cyclic molecules is often attributed to their ability to delocalize electrons across the ring, reducing overall energy and enhancing molecular robustness compared to their linear counterparts.
Biological Roles of Linear and Cyclic Molecules
Linear molecules, such as fatty acids and DNA strands, play crucial biological roles including energy storage, genetic information transmission, and structural functions within cells. Cyclic molecules, like glucose in its ring form and cyclic peptides, often exhibit enhanced stability and unique reactivity important for metabolic processes and signaling pathways. The distinct conformations of linear and cyclic molecules influence their interactions with enzymes and receptors, thereby determining their specific biological activities.
Synthesis Methods: Linear and Cyclic Pathways
Linear synthesis methods involve a sequential addition of monomers to form polymers with a straightforward chain growth, typically resulting in predictable molecular weights and structures. Cyclic synthesis pathways create ring-shaped polymers through intramolecular reactions, enhancing properties such as thermal stability and resistance to degradation. Techniques like ring-closing metathesis are pivotal in cyclic synthesis, while step-growth and chain-growth polymerizations are commonly employed in linear polymer formation.
Physical Properties Comparison: Linear vs Cyclic Structures
Linear molecular structures exhibit higher flexibility and lower steric hindrance compared to cyclic structures, resulting in greater elongation and tensile strength under stress. Cyclic compounds possess enhanced rigidity, leading to increased melting points and chemical stability due to ring strain and restricted rotational freedom. The compact geometry of cyclic molecules also influences solubility and intermolecular interactions, differentiating their physical properties significantly from linear analogs.
Applications in Industry: Linear vs Cyclic Uses
Linear processes dominate in industries requiring straightforward, step-by-step operations, such as automotive assembly lines and traditional manufacturing where sequential tasks ensure efficiency. Cyclic processes excel in sectors like pharmaceuticals and chemical production, where repetitive cycles facilitate quality control and continuous product output. Both methods optimize resource usage, but selection depends on industry-specific demands for precision, scalability, and workflow complexity.
Advantages and Limitations of Linear and Cyclic Systems
Linear systems offer straightforward implementation and predictable performance, making them ideal for applications requiring simplicity and ease of analysis, but they often suffer from limited flexibility and scalability. Cyclic systems provide enhanced adaptability and better resource utilization through repetition and feedback mechanisms, yet they can introduce complexity and require more sophisticated control strategies. Understanding the trade-offs between the simplicity of linear systems and the dynamic advantages of cyclic systems is crucial for optimizing system design based on specific operational needs.
Conclusion: Choosing Between Linear and Cyclic Designs
Selecting between linear and cyclic designs depends on project goals and data characteristics; linear designs excel in straightforward, sequential processes with clear cause-effect relationships, while cyclic designs are ideal for iterative, evolving systems requiring continuous feedback and refinement. Linear approaches provide simplicity and ease of analysis, whereas cyclic models enhance adaptability and ongoing improvement through repeated cycles. The decision hinges on whether predictability or flexibility is paramount for the given application and environment.
Linear Infographic
 libterm.com
libterm.com