Map projection transforms the Earth's three-dimensional surface onto a two-dimensional plane, balancing distortions in area, shape, distance, or direction. Different types of projections, such as Mercator, Robinson, and Lambert, serve various purposes depending on the geographic needs and accuracy required. Discover how understanding map projections enhances your ability to interpret maps accurately by reading the rest of this article.
Table of Comparison
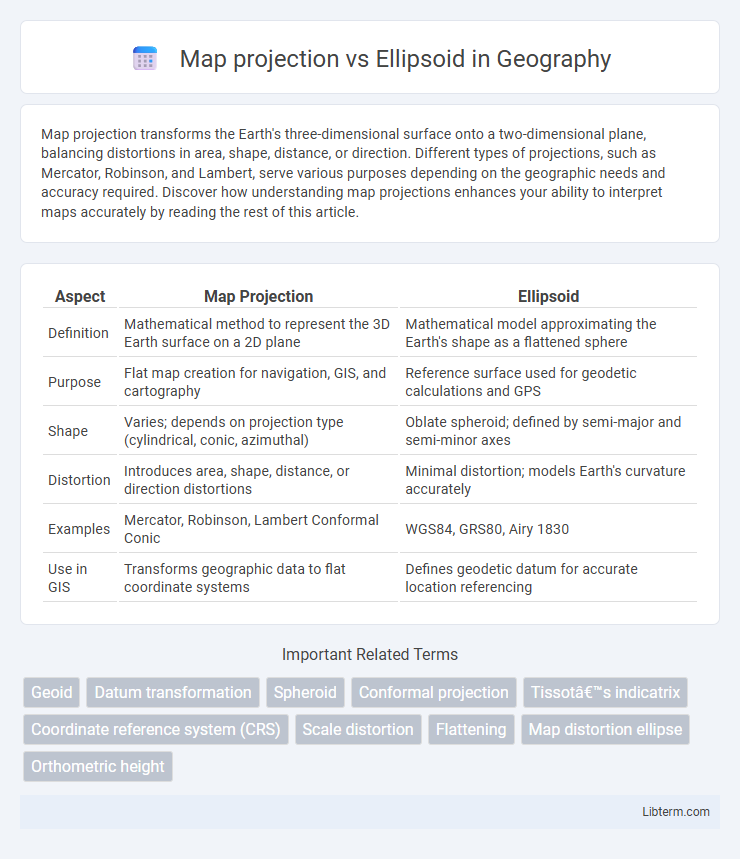
| Aspect | Map Projection | Ellipsoid |
|---|---|---|
| Definition | Mathematical method to represent the 3D Earth surface on a 2D plane | Mathematical model approximating the Earth's shape as a flattened sphere |
| Purpose | Flat map creation for navigation, GIS, and cartography | Reference surface used for geodetic calculations and GPS |
| Shape | Varies; depends on projection type (cylindrical, conic, azimuthal) | Oblate spheroid; defined by semi-major and semi-minor axes |
| Distortion | Introduces area, shape, distance, or direction distortions | Minimal distortion; models Earth's curvature accurately |
| Examples | Mercator, Robinson, Lambert Conformal Conic | WGS84, GRS80, Airy 1830 |
| Use in GIS | Transforms geographic data to flat coordinate systems | Defines geodetic datum for accurate location referencing |
Introduction to Map Projections and Ellipsoids
Map projections are mathematical techniques used to represent the curved surface of the Earth onto a flat map, each with varying degrees of distortion in area, shape, distance, or direction. Ellipsoids are simplified, mathematical representations of the Earth's shape, approximating its slightly flattened sphere form to serve as a reference surface for geodetic calculations. Understanding the relationship between map projections and ellipsoids is essential for accurate spatial data representation and geographic information systems (GIS).
Defining Map Projections
Map projections are mathematical methods used to transform the curved surface of the Earth, represented by an ellipsoid, onto a flat plane. These projections involve systematically transferring latitudes and longitudes from the ellipsoid model to a two-dimensional map, inherently introducing distortions in area, shape, distance, or direction. The choice of map projection depends on balancing these distortions to best suit the specific geographic and analytical needs of the map's purpose.
Understanding Geodetic Ellipsoids
A geodetic ellipsoid is a mathematically defined surface approximating the shape of the Earth, serving as a reference for latitude, longitude, and elevation measurements in mapping and geodesy. Map projections transform this three-dimensional ellipsoid onto a two-dimensional plane, introducing distortions in area, shape, distance, or direction. Understanding geodetic ellipsoids is crucial for accurate coordinate systems and spatial data representation, as they define the baseline for the projection's distortion characteristics.
Key Differences Between Map Projections and Ellipsoids
Map projections transform the Earth's three-dimensional ellipsoid surface into a two-dimensional plane, causing unavoidable distortions in area, shape, distance, or direction. Ellipsoids represent an idealized, mathematically defined shape of the Earth that approximates its geoid, used as a reference for geographic coordinate systems. Unlike ellipsoids that model the Earth's shape, map projections enable practical mapping by converting curved surfaces to flat maps, each with specific distortion characteristics tailored to different mapping needs.
Purpose and Importance of Map Projections
Map projections transform the curved surface of an ellipsoid, which approximates Earth's shape, onto a flat plane for practical use in maps and spatial analysis. This process is crucial for accurate distance, direction, and area representation in cartography, enabling navigation, geographic information systems (GIS), and land surveying. Understanding the distortions introduced by different projections allows specialists to select the most appropriate method for specific geographic applications and preserve essential spatial properties.
Role of Ellipsoids in Geodesy
Ellipsoids serve as mathematical models approximating Earth's shape to accurately represent its curved surface in geodesy, providing a standardized reference for latitude, longitude, and elevation measurements. Unlike map projections, which transform the ellipsoid's curved surface onto a flat plane, ellipsoids maintain the three-dimensional integrity essential for precise geodetic calculations and satellite positioning systems. The choice of an ellipsoid affects the accuracy of geospatial data and underpins global navigation frameworks such as WGS84 and GRS80.
Common Types of Map Projections
Map projections are mathematical methods used to represent the curved surface of the Earth (modeled as an ellipsoid) on a flat map, causing distortions in area, shape, distance, or direction. Common types of map projections include Mercator, which preserves angles for navigation but distorts size near poles; Lambert Conformal Conic, ideal for mid-latitude regions maintaining shape; and Robinson projection, which offers a compromise by reducing overall distortion. The choice of projection depends on the map's purpose, balancing the ellipsoid's geometric accuracy with the desired spatial properties on a two-dimensional plane.
Frequently Used Ellipsoid Models
Frequently used ellipsoid models such as WGS84, GRS80, and Airy1830 provide standardized mathematical representations of the Earth's shape, crucial for accurate geospatial data referencing. Map projections transform these ellipsoidal coordinates onto flat surfaces, each projection optimizing for specific spatial properties like area, shape, distance, or direction. Selecting an appropriate ellipsoid model ensures consistency and precision in global positioning systems, satellite navigation, and cartographic mapping applications.
Impact on Geographic Data Accuracy
Map projections transform the curved surface of an ellipsoid-shaped Earth into a flat plane, inherently introducing distortions in scale, area, shape, or distance. The choice of ellipsoid, defined by its semi-major and semi-minor axes, directly influences the baseline accuracy of geographic coordinates before projection. Variations between different ellipsoids can cause discrepancies of several meters in positioning, which are further compounded by distortions from the chosen map projection, impacting precision in applications such as surveying and navigation.
Choosing the Right Map Projection and Ellipsoid
Choosing the right map projection depends on the specific purpose of the map, such as preserving area, shape, distance, or direction, while selecting the appropriate ellipsoid is crucial for accurate geodetic calculations based on the Earth's shape. Popular ellipsoids like WGS84, GRS80, and Clarke 1866 provide different parameters for flattening and ellipsoid radii, impacting spatial accuracy and fit to the geoid in various regions. Combining a suitable ellipsoid with an appropriate map projection, such as Mercator for navigation or Albers Equal-Area for regional planning, ensures optimal representation and minimal spatial distortion.
Map projection Infographic
 libterm.com
libterm.com