A coordinate system allows you to precisely locate points in space using numerical values, typically represented as pairs or triples of coordinates. Understanding how each axis functions and interacts is essential for applications in mathematics, physics, engineering, and computer graphics. Explore the rest of this article to uncover detailed explanations and practical examples of coordinate systems in action.
Table of Comparison
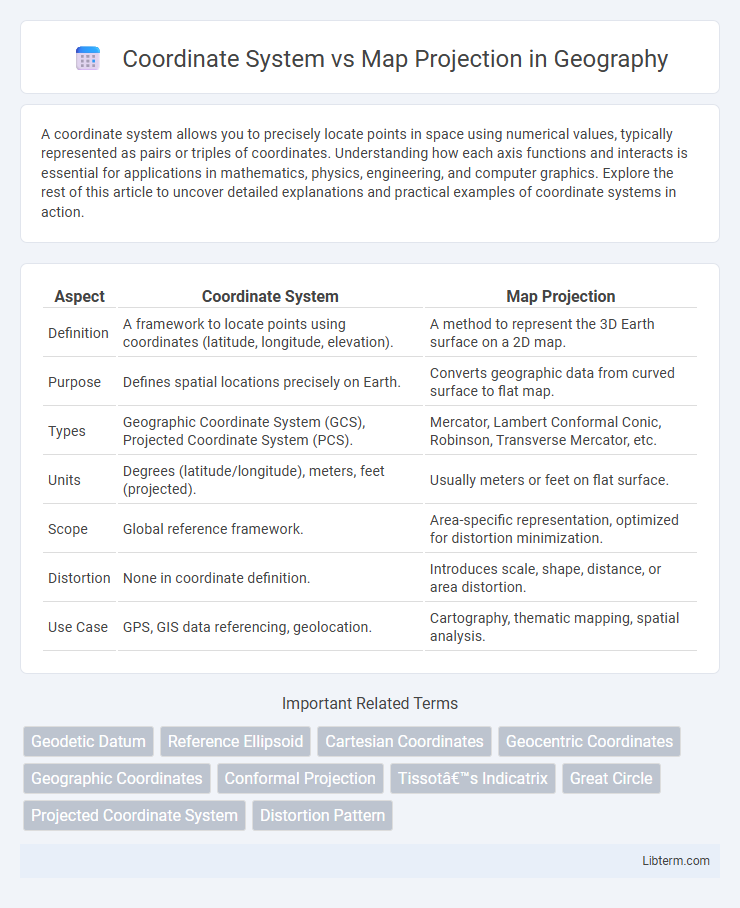
| Aspect | Coordinate System | Map Projection |
|---|---|---|
| Definition | A framework to locate points using coordinates (latitude, longitude, elevation). | A method to represent the 3D Earth surface on a 2D map. |
| Purpose | Defines spatial locations precisely on Earth. | Converts geographic data from curved surface to flat map. |
| Types | Geographic Coordinate System (GCS), Projected Coordinate System (PCS). | Mercator, Lambert Conformal Conic, Robinson, Transverse Mercator, etc. |
| Units | Degrees (latitude/longitude), meters, feet (projected). | Usually meters or feet on flat surface. |
| Scope | Global reference framework. | Area-specific representation, optimized for distortion minimization. |
| Distortion | None in coordinate definition. | Introduces scale, shape, distance, or area distortion. |
| Use Case | GPS, GIS data referencing, geolocation. | Cartography, thematic mapping, spatial analysis. |
Introduction to Coordinate Systems and Map Projections
Coordinate systems are frameworks that use numerical values, such as latitude and longitude, to precisely locate points on the Earth's surface. Map projections transform the three-dimensional Earth into a two-dimensional representation, preserving specific spatial properties like area, shape, distance, or direction based on the chosen projection method. Understanding the relationship between coordinate systems and map projections is essential for accurate geographic data visualization and spatial analysis.
Defining Coordinate Systems
Defining coordinate systems involves establishing a framework for specifying locations on the Earth's surface through latitude, longitude, and elevation values based on a reference datum like WGS84 or NAD83. These systems provide a consistent method to measure and represent spatial data, enabling accurate geographic positioning and navigation. Unlike map projections, which transform the curved Earth's surface into a flat map, coordinate systems serve as the fundamental basis for spatial referencing and georeferencing in GIS applications.
Understanding Map Projections
Map projections are methods used to represent the curved surface of the Earth on a flat plane, transforming geographic coordinates from a spherical coordinate system into a two-dimensional map. Each projection introduces distortions in area, shape, distance, or direction, with common types including Mercator, Robinson, and Lambert conformal conic projections, each tailored for specific mapping purposes. Understanding the selection and limitations of map projections is crucial in geospatial analysis to ensure accurate spatial representation and interpretation.
Key Differences Between Coordinate Systems and Map Projections
Coordinate systems define how locations are represented using numeric coordinates, typically in a three-dimensional space such as latitude, longitude, and elevation, while map projections transform the curved surface of the Earth onto a flat plane, causing distortions in area, shape, distance, or direction. Coordinate systems serve as a foundational reference framework for spatial data, whereas map projections manipulate that data to create flat maps optimized for specific purposes like navigation or analysis. Understanding these distinctions is crucial for selecting the appropriate spatial reference method in geospatial applications and cartography.
Types of Coordinate Systems
Types of coordinate systems include geographic coordinate systems (GCS), which use latitude and longitude based on a spherical model of the Earth, and projected coordinate systems (PCS), which transform the curved surface into a flat map using mathematical projections. Geographic coordinate systems provide global positioning using angular measurements, while projected coordinate systems offer planar coordinates such as eastings and northings tailored for specific regions. Common examples of projected systems include Universal Transverse Mercator (UTM) and State Plane Coordinate System (SPCS), designed to minimize distortions on flat maps.
Common Map Projection Methods
Common map projection methods include Mercator, Robinson, and Lambert Conformal Conic, each designed to represent the curved surface of the Earth on a flat map with varying levels of distortion in area, shape, distance, or direction. The Mercator projection preserves angles and shapes near the equator, making it useful for navigation, while the Robinson projection balances size and shape distortion for visually appealing world maps. Lambert Conformal Conic projection is widely used for aeronautical charts and mid-latitude regions due to its accurate representation of shapes and distances along standard parallels.
Applications of Coordinate Systems in GIS
Coordinate systems in GIS provide a framework for precisely locating geographic features on the Earth's surface, essential for spatial data integration and analysis. They enable accurate measurement, navigation, and spatial querying by defining coordinates through latitude and longitude or other units, facilitating applications like urban planning, environmental monitoring, and disaster management. Effective use of coordinate systems ensures consistency and interoperability across diverse GIS datasets and mapping platforms.
Impact of Map Projections on Spatial Accuracy
Map projections significantly impact spatial accuracy by transforming the curved surface of the Earth onto a flat plane, introducing distortions in area, shape, distance, or direction. Common projections like Mercator preserve angles but distort size, causing misrepresentation of landmass proportions, particularly near the poles. Choosing an appropriate map projection based on the intended use, such as equal-area or conformal, is crucial for maintaining spatial accuracy in geographic analyses and cartographic representations.
Choosing the Right Coordinate System and Map Projection
Choosing the right coordinate system and map projection depends on the geographic area, purpose, and scale of the project, ensuring accurate spatial data representation. Coordinate systems like Geographic Coordinate System (GCS) use latitude and longitude for global reference, while Projected Coordinate Systems (PCS) such as UTM or State Plane provide flat, two-dimensional maps with minimized distortion. Evaluating factors like projection type (conformal, equal-area, equidistant), distortion tolerance, and application requirements ensures optimal spatial analysis and mapping precision.
Conclusion: Integrating Coordinate Systems with Map Projections
Integrating coordinate systems with map projections is essential for accurately representing the Earth's curved surface on flat maps, ensuring spatial data consistency and precision. Coordinate systems provide a framework for locating points globally using latitude, longitude, and elevation, while map projections translate these three-dimensional coordinates onto two-dimensional planes by minimizing distortions in area, shape, distance, or direction. Effective geographic data analysis relies on selecting compatible coordinate systems and map projections tailored to specific regional or thematic mapping needs.
Coordinate System Infographic
 libterm.com
libterm.com