Lie algebra, a fundamental concept in abstract algebra, studies algebraic structures essential for understanding continuous transformation groups and symmetries in mathematics and physics. Its applications range from quantum mechanics to differential geometry, providing tools for analyzing complex systems. Explore the article to uncover how Lie algebra can deepen your grasp of mathematical structures and their real-world implications.
Table of Comparison
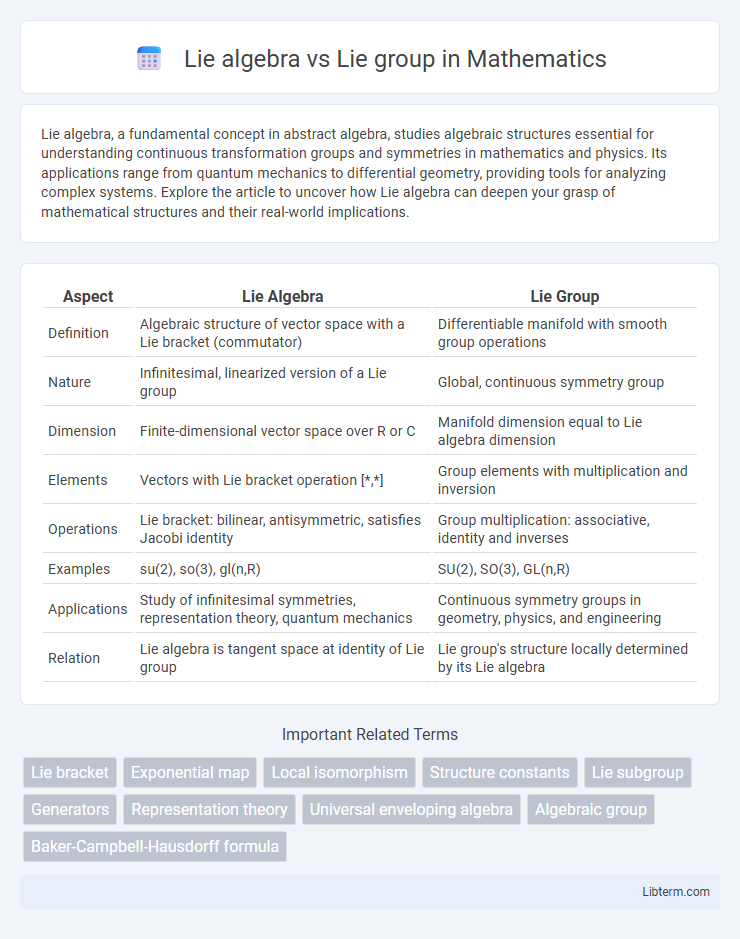
| Aspect | Lie Algebra | Lie Group |
|---|---|---|
| Definition | Algebraic structure of vector space with a Lie bracket (commutator) | Differentiable manifold with smooth group operations |
| Nature | Infinitesimal, linearized version of a Lie group | Global, continuous symmetry group |
| Dimension | Finite-dimensional vector space over R or C | Manifold dimension equal to Lie algebra dimension |
| Elements | Vectors with Lie bracket operation [*,*] | Group elements with multiplication and inversion |
| Operations | Lie bracket: bilinear, antisymmetric, satisfies Jacobi identity | Group multiplication: associative, identity and inverses |
| Examples | su(2), so(3), gl(n,R) | SU(2), SO(3), GL(n,R) |
| Applications | Study of infinitesimal symmetries, representation theory, quantum mechanics | Continuous symmetry groups in geometry, physics, and engineering |
| Relation | Lie algebra is tangent space at identity of Lie group | Lie group's structure locally determined by its Lie algebra |
Introduction to Lie Algebras and Lie Groups
Lie algebras and Lie groups are fundamental structures in mathematics and theoretical physics, with Lie groups representing continuous symmetry transformations and Lie algebras capturing their infinitesimal properties through vector spaces equipped with a Lie bracket. The correspondence between Lie groups and Lie algebras is established by the exponential map, linking Lie algebra elements to local group elements near the identity, allowing for the study of group behavior via algebraic methods. Lie algebras provide a linearized, algebraic framework to analyze the local structure of Lie groups, facilitating classification, representation theory, and applications in geometry and quantum mechanics.
Definitions: What Are Lie Algebras?
Lie algebras are algebraic structures consisting of a vector space equipped with a bilinear, antisymmetric operation called the Lie bracket, which satisfies the Jacobi identity. They serve as the tangent space at the identity element of a Lie group, capturing the group's infinitesimal symmetries. Lie algebras provide a linearized framework for studying the local behavior and structure of Lie groups.
Definitions: What Are Lie Groups?
Lie groups are smooth manifolds equipped with group operations of multiplication and inversion that are differentiable, combining algebraic and geometric structures. They serve as continuous symmetry groups instrumental in analyzing differential equations, geometry, and physics. Lie algebras arise as tangent spaces at the identity element of Lie groups, encoding the infinitesimal structure and facilitating the study of their local properties.
Historical Development of Lie Theory
The historical development of Lie theory began in the late 19th century with Sophus Lie's work on continuous transformation groups, where Lie algebras emerged as the algebraic structures underlying Lie groups. Early contributions by Wilhelm Killing and Elie Cartan further established the classification and structure theory of Lie algebras, enhancing the understanding of Lie groups in geometry and physics. The interplay between Lie groups and Lie algebras became foundational for modern developments in differential geometry, representation theory, and theoretical physics.
Structural Differences Between Lie Algebras and Lie Groups
Lie algebras are algebraic structures characterized by a vector space equipped with a Lie bracket, encapsulating infinitesimal symmetries, while Lie groups are smooth manifolds with a group structure representing continuous symmetries. The key structural difference lies in Lie groups possessing a global nonlinear structure allowing group operations, whereas Lie algebras capture local linearized behavior near the identity element through commutation relations. Lie algebras serve as the tangent space at the identity of Lie groups, providing a linear approximation of the group's structure but lacking the global topological and manifold properties inherent to Lie groups.
Algebraic Properties: Commutators vs Group Operations
Lie algebras encode the algebraic structure of Lie groups through commutators, which measure the non-commutativity of elements in an infinitesimal neighborhood of the identity. Lie group operations follow smooth manifold structures with associative multiplication and inverses, while their Lie algebras capture local linear approximations via the Lie bracket. The commutator in Lie algebras reflects the infinitesimal generators of group operations, providing a linearized framework to study continuous symmetries and group dynamics.
Role of Lie Algebra as Tangent Space of Lie Group
Lie algebra serves as the tangent space at the identity element of a Lie group, capturing the group's local infinitesimal structure through a vector space equipped with a Lie bracket. This correspondence allows the exponential map to link Lie algebra elements to Lie group elements, enabling the study of global group properties via local algebraic data. The tangent space framework provides a powerful tool for analyzing continuous symmetries and differential geometric aspects of Lie groups.
Applications in Mathematics and Physics
Lie algebras provide a powerful algebraic framework for studying the local structure of Lie groups, enabling mathematicians to analyze continuous symmetry through infinitesimal generators. In physics, Lie groups describe global symmetries of physical systems, such as rotational invariance in quantum mechanics, while their corresponding Lie algebras facilitate the computation of conserved quantities and the formulation of gauge theories. The interplay between Lie groups and Lie algebras underpins advanced topics including particle classification, symmetry breaking, and the integration of differential equations in both classical and quantum field theories.
Examples: Classic Lie Groups and Their Algebras
Classic Lie groups include the rotation group SO(3), representing rotations in three-dimensional space, and its associated Lie algebra so(3), consisting of skew-symmetric 3x3 matrices. The special linear group SL(n, R), composed of nxn real matrices with determinant one, corresponds to the Lie algebra sl(n, R), characterized by traceless nxn matrices. These examples illustrate the connection between Lie groups as smooth manifolds with group structures and Lie algebras as their tangent spaces at the identity element, encoding infinitesimal symmetries.
Summary: When to Use Lie Algebras vs Lie Groups
Lie algebras are utilized primarily for analyzing the infinitesimal structure and local properties of continuous symmetry groups represented by Lie groups, providing a linearized framework that simplifies complex calculations. Lie groups, on the other hand, capture the global geometric and topological aspects of continuous symmetries, making them essential for studying finite transformations and group actions on manifolds. Use Lie algebras when working with differential equations, local behavior, or representations, and employ Lie groups for global symmetry considerations and nonlinear transformations.
Lie algebra Infographic
 libterm.com
libterm.com