Arithmetic mean is the sum of a set of numerical values divided by the number of values in the set, providing a measure of central tendency. It is widely used in statistics to analyze data distributions and summarize key information efficiently. Explore the rest of the article to understand how arithmetic mean applies to your data and its practical implications.
Table of Comparison
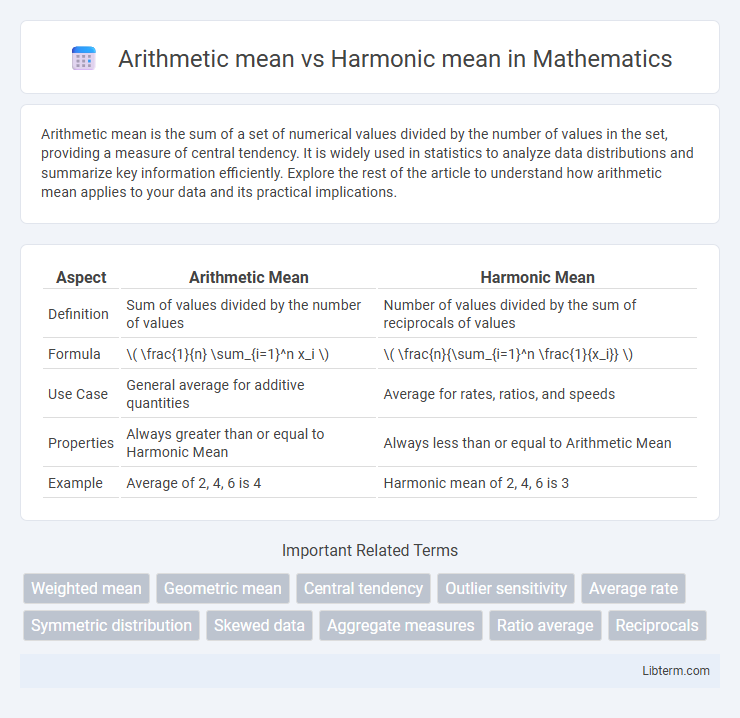
| Aspect | Arithmetic Mean | Harmonic Mean |
|---|---|---|
| Definition | Sum of values divided by the number of values | Number of values divided by the sum of reciprocals of values |
| Formula | \( \frac{1}{n} \sum_{i=1}^n x_i \) | \( \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \) |
| Use Case | General average for additive quantities | Average for rates, ratios, and speeds |
| Properties | Always greater than or equal to Harmonic Mean | Always less than or equal to Arithmetic Mean |
| Example | Average of 2, 4, 6 is 4 | Harmonic mean of 2, 4, 6 is 3 |
Introduction to Arithmetic Mean and Harmonic Mean
The arithmetic mean is a measure of central tendency calculated by summing a set of values and dividing by their count, often used for data with additive relationships. The harmonic mean, in contrast, is the reciprocal of the average of reciprocals, best suited for rates and ratios such as speeds or densities. Understanding when to apply the arithmetic mean versus the harmonic mean is essential for accurate data analysis in fields like finance, physics, and statistics.
Defining Arithmetic Mean
The arithmetic mean, often called the average, is calculated by summing all values in a dataset and dividing by the number of observations. It provides a central measure that represents the typical value of a set of numbers, especially useful for data with additive properties. Unlike the harmonic mean, which is more appropriate for rates and ratios, the arithmetic mean is sensitive to outliers and larger values.
Understanding Harmonic Mean
Harmonic mean is a measure of central tendency calculated as the reciprocal of the arithmetic mean of the reciprocals of a data set, making it particularly useful for rates and ratios such as speed or density. Unlike the arithmetic mean, which sums values directly, the harmonic mean gives greater weight to smaller numbers, providing a more accurate average when dealing with quantities that are inversely related. This characteristic makes the harmonic mean essential in fields like finance, physics, and engineering where averaging rates or ratios is required for meaningful analysis.
Key Differences Between Arithmetic and Harmonic Means
Arithmetic mean calculates the average by summing all values and dividing by the number of values, emphasizing equal weight for each data point. Harmonic mean, on the other hand, is computed as the reciprocal of the average of reciprocals of the data set, which gives greater weight to smaller values. Key differences include arithmetic mean being suitable for additive data, while harmonic mean is ideal for rates and ratios, especially when averaging quantities like speed or density.
Mathematical Formulas and Calculation Methods
The arithmetic mean is calculated by summing all values and dividing by the number of values, represented as \(\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\). The harmonic mean is defined as the reciprocal of the average of the reciprocals of the values, given by \(H = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}}\). While the arithmetic mean emphasizes equal weighting of values, the harmonic mean is particularly useful for rates and ratios, giving more weight to smaller values in the dataset.
Practical Applications of Arithmetic Mean
The arithmetic mean is widely used in practical applications such as calculating average income, test scores, and population growth rates, providing a straightforward measure of central tendency for data sets. It helps in making financial decisions by averaging costs or returns over time, which is essential for budgeting and investment analysis. Unlike the harmonic mean, which is more suited for rates and ratios, the arithmetic mean is ideal for additive data and gives a balanced representation of typical values.
When to Use Harmonic Mean
The harmonic mean is most appropriate for averaging rates or ratios, especially when dealing with quantities like speeds or densities where the denominator varies. It provides a more accurate average when the data involves rates over a fixed unit, such as average speed over multiple segments or cost per unit. Use the harmonic mean to avoid skewed results that can occur with the arithmetic mean when averaging values with unequal denominators.
Case Studies: Comparing Both Means in Real Scenarios
Case studies comparing arithmetic mean and harmonic mean often highlight differences in accuracy depending on data type; for example, harmonic mean provides better insights in rate-based scenarios like average speed or fuel efficiency where reciprocal relationships dominate. When calculating average prices or simple data averages, the arithmetic mean accurately reflects central tendency, but it can misrepresent values in proportional datasets where harmonic mean offers more precise aggregation. Real-world applications such as financial cost averaging and performance evaluation demonstrate that choosing between arithmetic and harmonic means significantly impacts analysis outcomes and decision-making.
Advantages and Limitations of Each Mean
The arithmetic mean provides a straightforward average that is easy to compute and interpret, making it ideal for datasets with values of similar magnitude and no extreme outliers. Its limitation lies in sensitivity to large outliers, which can skew the result and misrepresent the central tendency. The harmonic mean excels in averaging rates or ratios, such as speeds or densities, offering a more accurate central value when dealing with reciprocal quantities, but it becomes less meaningful or undefined when the dataset contains zero or negative values.
Conclusion: Choosing the Right Mean for Your Data
Selecting the arithmetic mean is ideal for datasets with values consistently distributed and no extreme outliers, as it accurately represents the average. The harmonic mean suits situations involving rates or ratios, especially when smaller values disproportionately influence the average, providing a more balanced measure. Evaluating the nature of your data and the specific context ensures the appropriate mean enhances meaningful analysis and decision-making.
Arithmetic mean Infographic
 libterm.com
libterm.com