Hyperkahler manifolds are special types of Riemannian manifolds equipped with three complex structures satisfying quaternionic relations, which induce a rich geometric and topological structure. These manifolds play a crucial role in mathematical physics and differential geometry, providing deep insights into moduli spaces and supersymmetric gauge theories. Explore the rest of the article to uncover the intricate properties and applications of hyperkahler manifolds in modern mathematics.
Table of Comparison
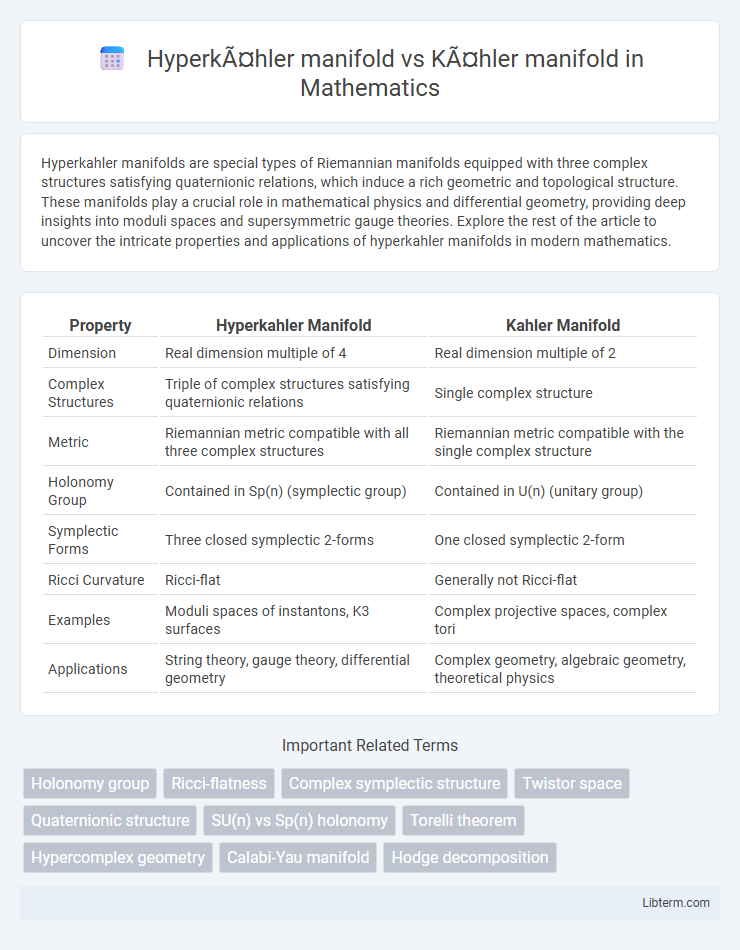
| Property | Hyperkahler Manifold | Kahler Manifold |
|---|---|---|
| Dimension | Real dimension multiple of 4 | Real dimension multiple of 2 |
| Complex Structures | Triple of complex structures satisfying quaternionic relations | Single complex structure |
| Metric | Riemannian metric compatible with all three complex structures | Riemannian metric compatible with the single complex structure |
| Holonomy Group | Contained in Sp(n) (symplectic group) | Contained in U(n) (unitary group) |
| Symplectic Forms | Three closed symplectic 2-forms | One closed symplectic 2-form |
| Ricci Curvature | Ricci-flat | Generally not Ricci-flat |
| Examples | Moduli spaces of instantons, K3 surfaces | Complex projective spaces, complex tori |
| Applications | String theory, gauge theory, differential geometry | Complex geometry, algebraic geometry, theoretical physics |
Introduction to Kähler and Hyperkähler Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated (1,1)-form is closed, integrating symplectic and complex structures harmoniously. Hyperkahler manifolds extend this structure by possessing a triple of complex structures satisfying quaternionic relations, all compatible with a single Riemannian metric, resulting in a richer geometric framework. These manifolds play a crucial role in differential geometry and theoretical physics, particularly in supersymmetry and string theory.
Defining Kähler Manifolds: Structure and Properties
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated 2-form is closed, satisfying the Kahler condition and thus integrating symplectic, complex, and Riemannian structures. The Kahler form o defines a non-degenerate, closed 2-form compatible with the complex structure J, ensuring that the metric g is Hermitian and parallel with respect to the Levi-Civita connection. This rich geometric framework enables Kahler manifolds to exhibit properties such as Ricci curvature determined by the first Chern class and Hodge decomposition, fundamental in both algebraic geometry and theoretical physics.
Fundamentals of Hyperkähler Manifolds
Hyperkahler manifolds are a special class of Kahler manifolds characterized by the presence of three complex structures satisfying the quaternionic relations and a metric that is Kahler with respect to each complex structure. These manifolds are Ricci-flat and admit a hyperkahler metric, making them important in differential geometry and theoretical physics, especially in supersymmetry and string theory. The fundamental properties of hyperkahler manifolds include their holonomy group being contained in Sp(n), which distinguishes them from general Kahler manifolds whose holonomy lies in U(n).
Key Differences: Kähler vs Hyperkähler Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated 2-form is closed, enabling rich geometric and algebraic structures such as Hodge decomposition and Ricci curvature analysis. Hyperkahler manifolds extend this concept by possessing three complex structures obeying quaternionic relations and a metric that is Kahler with respect to each, yielding a richer geometric framework with a holonomy group contained in Sp(n). The key differences lie in the manifold's holonomy group, the presence of multiple complex structures in hyperkahler manifolds, and the resulting implications for topology and geometry, like enhanced symmetry and stronger restrictions on curvature.
Complex Structures in Kähler and Hyperkähler Geometry
A Kahler manifold is a complex manifold equipped with a Hermitian metric whose associated 2-form is closed, combining complex, symplectic, and Riemannian geometry. Hyperkahler manifolds possess not just one but a triple of complex structures satisfying the quaternionic relations, with each complex structure compatible with the same Riemannian metric and symplectic form. This rich structure leads to a unique interplay between complex, symplectic, and hypercomplex geometries, distinguishing hyperkahler geometry from the single complex structure framework of Kahler manifolds.
Symplectic Forms: Comparing Kähler and Hyperkähler Cases
Kahler manifolds are equipped with a single symplectic form compatible with a complex structure and a Riemannian metric, providing a rich interplay between geometry and topology. Hyperkahler manifolds extend this framework by possessing a triplet of symplectic forms corresponding to a quaternionic triple of complex structures that satisfy the relations of the quaternion algebra. This tri-symplectic structure endows hyperkahler manifolds with enhanced geometric rigidity and richer holonomy, typically SU(2) or Sp(n), compared to the simpler U(n) holonomy of Kahler manifolds.
Holonomy Groups: Unique Characteristics
Hyperkahler manifolds have holonomy groups strictly contained within Sp(n), reflecting their rich quaternionic structure, while Kahler manifolds feature holonomy in U(n), corresponding to complex structures with compatible symplectic forms. The restricted holonomy of hyperkahler manifolds ensures Ricci-flatness and the presence of parallel complex structures, contrasting with the broader variety of holonomy types possible in the Kahler category. This unique holonomy characteristic governs geometric and topological properties, influencing moduli spaces and the type of differential equations these manifolds can support.
Examples of Kähler and Hyperkähler Manifolds
Examples of Kahler manifolds include complex projective spaces such as CP^n, complex tori, and smooth projective algebraic varieties endowed with the Fubini-Study metric. Hyperkahler manifolds, exhibiting richer geometric structures, include the flat quaternionic space H^n, K3 surfaces, and certain moduli spaces of Higgs bundles or instantons. While all hyperkahler manifolds are Kahler, typical examples of Kahler manifolds like complex projective spaces do not possess the additional quaternionic structures required for hyperkahler geometry.
Applications in Mathematics and Physics
Hyperkahler manifolds, equipped with a triple of complex structures satisfying quaternionic relations, generalize Kahler manifolds and find crucial applications in gauge theory, particularly in moduli spaces of solutions to anti-self-dual Yang-Mills equations. Kahler manifolds, characterized by a symplectic form compatible with a complex structure and Riemannian metric, serve as foundational models in algebraic geometry and complex differential geometry, underpinning Hodge theory and mirror symmetry. In theoretical physics, hyperkahler geometry is instrumental in supersymmetric sigma models and string theory compactifications, while Kahler structures are essential in the study of Calabi-Yau manifolds and stability conditions in geometric invariant theory.
Conclusion: Choosing Between Kähler and Hyperkähler Manifolds
Choosing between Kahler and Hyperkahler manifolds depends on the geometric and physical context, where Kahler manifolds provide a rich structure combining complex, symplectic, and Riemannian features suited for a broad range of applications in complex geometry and theoretical physics. Hyperkahler manifolds, characterized by their quaternionic structure and special holonomy SU(2), offer more stringent conditions and are crucial in studying supersymmetric gauge theories and string theory compactifications. The decision hinges on the necessity of enhanced symmetry and dimensional constraints, with Hyperkahler manifolds serving specialized purposes beyond the more general and versatile Kahler geometry.
Hyperkähler manifold Infographic
 libterm.com
libterm.com