Radius of curvature measures the radius of the circular arc that best approximates a curve at a specific point, reflecting its bending degree. This geometric concept is vital in fields such as physics, engineering, and computer graphics, where understanding the curve's sharpness influences design and analysis. Explore the rest of the article to discover how accurately calculating your curve's radius of curvature can enhance practical applications.
Table of Comparison
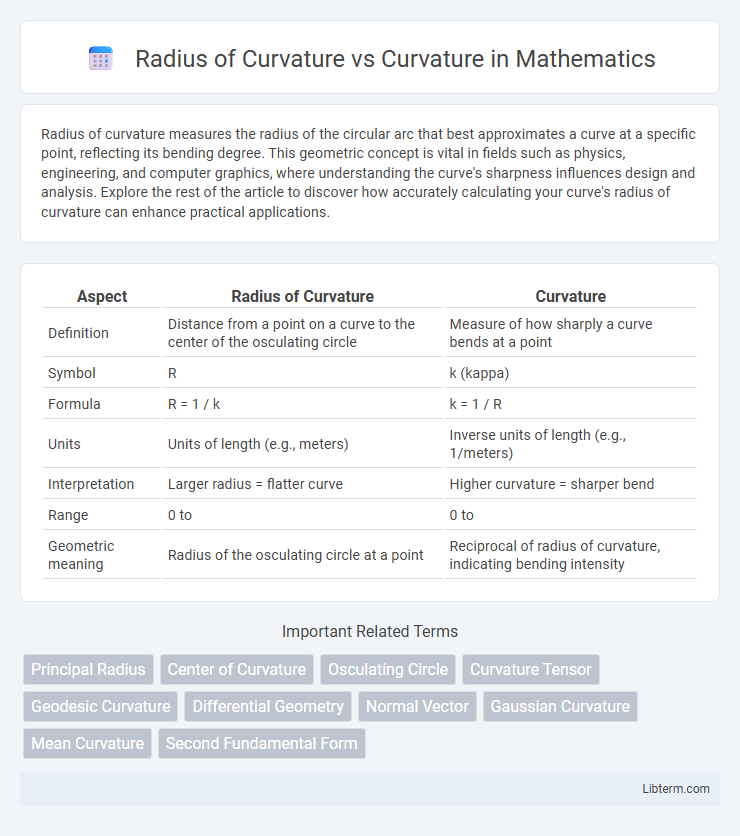
| Aspect | Radius of Curvature | Curvature |
|---|---|---|
| Definition | Distance from a point on a curve to the center of the osculating circle | Measure of how sharply a curve bends at a point |
| Symbol | R | k (kappa) |
| Formula | R = 1 / k | k = 1 / R |
| Units | Units of length (e.g., meters) | Inverse units of length (e.g., 1/meters) |
| Interpretation | Larger radius = flatter curve | Higher curvature = sharper bend |
| Range | 0 to | 0 to |
| Geometric meaning | Radius of the osculating circle at a point | Reciprocal of radius of curvature, indicating bending intensity |
Introduction to Radius of Curvature and Curvature
Radius of curvature quantifies the radius of a circle that best approximates a curve at a specific point, serving as a fundamental measure of how sharply the curve bends. Curvature is the reciprocal of the radius of curvature and represents the rate at which the curve changes direction per unit length. These concepts are essential in fields like differential geometry, robotics, and mechanical engineering for analyzing and designing curved paths.
Definitions: What is Curvature?
Curvature measures how rapidly a curve deviates from being a straight line, defined as the rate of change of the tangent angle with respect to arc length. The radius of curvature is the reciprocal of curvature, representing the radius of the osculating circle that best approximates the curve at a given point. High curvature corresponds to a small radius of curvature, indicating a sharply bending curve.
Definitions: What is Radius of Curvature?
Radius of Curvature measures the radius of the osculating circle that best approximates a curve at a specific point, representing how sharply the curve bends. Curvature is the reciprocal of the Radius of Curvature, quantifying the amount of bending per unit length along the curve. A smaller Radius of Curvature indicates a tighter bend, while a larger radius signifies a gentler curve.
Mathematical Relationship Between Curvature and Radius of Curvature
Curvature (k) is mathematically defined as the reciprocal of the radius of curvature (R), expressed as k = 1/R. The radius of curvature represents the radius of the osculating circle that best approximates the curve at a particular point, inversely proportional to the rate of change of the tangent angle with respect to arc length. This fundamental relationship enables precise quantification of how sharply a curve bends, with smaller radii corresponding to higher curvature values.
Physical Interpretation: Curvature vs Radius of Curvature
Curvature quantifies how sharply a curve bends at a given point, mathematically defined as the reciprocal of the radius of curvature, indicating the degree of deviation from a straight line. The radius of curvature physically represents the radius of the osculating circle that best approximates the curve's local shape, providing an intuitive geometric measure of bending. Smaller radii correspond to higher curvature values, signifying tighter bends, while larger radii reflect gentler curves with lower curvature.
Calculation Methods for Curvature
Curvature is calculated as the reciprocal of the radius of curvature, representing how sharply a curve bends at a specific point, with units of inverse length (e.g., 1/m). The radius of curvature is determined geometrically by fitting osculating circles to the curve, where smaller radii indicate higher curvature values. Analytical methods for curvature calculation include using derivatives of curve equations, such as curvature k = |d2y/dx2| / (1 + (dy/dx)2)^(3/2) for planar curves, enabling precise curvature measurement in differential geometry and computer graphics.
Calculation Methods for Radius of Curvature
Radius of curvature is mathematically defined as the reciprocal of curvature, providing a direct geometric measure of how sharply a curve bends at a given point. Calculation methods for the radius of curvature typically involve differential geometry formulas, such as R = 1/k, where curvature k can be derived from the first and second derivatives of a parametric curve. Advanced techniques use the Frenet-Serret formulas or numerical approximations based on discrete point clouds in computational applications to estimate the radius precisely.
Practical Applications in Engineering and Physics
Radius of curvature and curvature are critical in engineering and physics for analyzing the bending of beams, roads, and lenses. Radius of curvature defines the radius of the osculating circle at a curve's point, directly influencing stress distribution in structural components and the focusing properties in optics. Curvature, the reciprocal of radius of curvature, quantifies how sharply a curve bends, essential for optimizing vehicle trajectories and material deformation predictions.
Graphical Representation and Visualization
The radius of curvature graphically represents the radius of the osculating circle at a point on a curve, appearing as a smooth, continuous function inversely related to the curvature, which measures the rate of change of the curve's direction. Visualization of curvature often involves plotting the curvature function k(s), where s is the arc length, highlighting points with high curvature as peaks, while the radius of curvature graph shows troughs corresponding to these peaks due to the inverse relationship \( R = \frac{1}{\kappa} \). Graphing both on the same axis provides a clear comparative view: curvature emphasizes sharpness at bends, while radius of curvature conveys the size of the circle best approximating the curve locally.
Summary: Key Differences and Similarities
Radius of curvature measures the radius of an osculating circle that best approximates a curve at a specific point, while curvature quantifies the rate at which the curve deviates from a straight line, mathematically defined as the reciprocal of the radius of curvature. Both concepts describe the bending of a curve but from inverse perspectives: curvature expresses the intensity of bending, and radius of curvature provides a geometric length scale of this bending. These entities are fundamental in differential geometry, used in disciplines such as physics, engineering, and computer graphics to analyze and design curves accurately.
Radius of Curvature Infographic
 libterm.com
libterm.com