Cocountable refers to mathematical concepts related to the size of infinite sets that can be paired one-to-one with the natural numbers, indicating a countable infinity. Understanding cocountable sets is essential in advanced set theory and helps clarify the distinction between different infinities in mathematics. Explore the rest of the article to deepen your knowledge of cocountable sets and their applications.
Table of Comparison
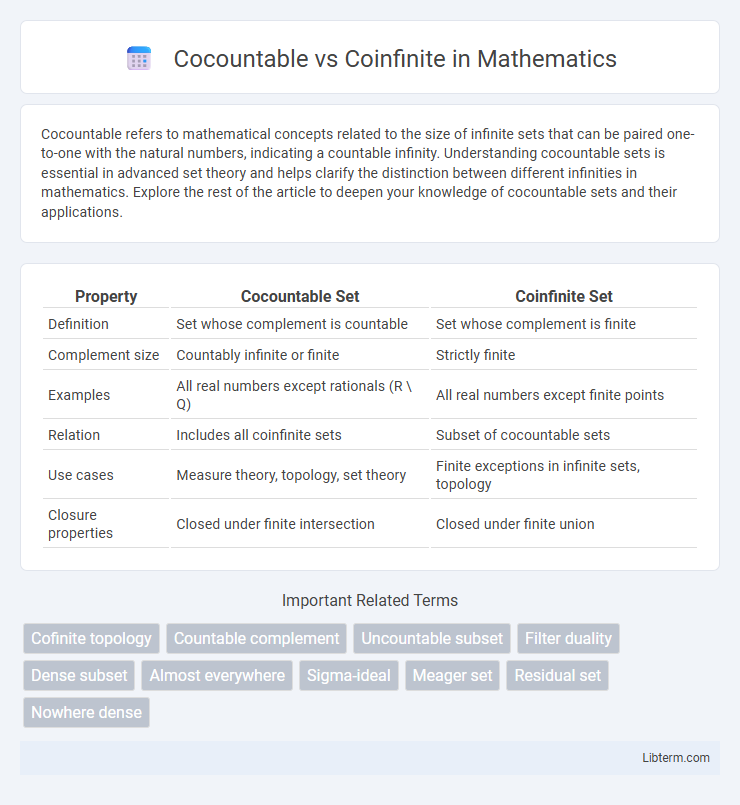
| Property | Cocountable Set | Coinfinite Set |
|---|---|---|
| Definition | Set whose complement is countable | Set whose complement is finite |
| Complement size | Countably infinite or finite | Strictly finite |
| Examples | All real numbers except rationals (R \ Q) | All real numbers except finite points |
| Relation | Includes all coinfinite sets | Subset of cocountable sets |
| Use cases | Measure theory, topology, set theory | Finite exceptions in infinite sets, topology |
| Closure properties | Closed under finite intersection | Closed under finite union |
Introduction to Cocountable and Coinfinite Sets
Cocountable sets are subsets of a given set whose complements are countable, meaning they contain either finitely many or countably infinite elements. Coinfinite sets, on the other hand, have complements that are finite, making them a specific case of cocountable sets with finite omissions. Understanding these concepts is essential in topology and measure theory, where cocountable and coinfinite sets aid in characterizing dense subsets and establishing foundational properties of infinite sets.
Defining Cocountable Sets
Cocountable sets are defined as subsets of a given set whose complements are countable, meaning they contain finitely or countably many elements. This property ensures that cocountable sets are "large" in terms of cardinality, contrasting with coinfinite sets, whose complements are infinite but not necessarily countable. Understanding cocountable sets is fundamental in topology and measure theory, where they play a key role in defining coarser topologies and sigma-algebras.
Understanding Coinfinite Sets
Coinfinite sets are characterized by their complements being countable, meaning the difference between the universal set and the coinfinite set contains a countable number of elements. These sets often arise in measure theory and real analysis, where their uncountable nature contrasts with the countability of their complement, emphasizing the subtle differences in infinite cardinalities. Understanding coinfinite sets aids in exploring properties of infinite sets that are "almost" whole, missing only countably many points from completeness.
Key Differences Between Cocountable and Coinfinite
Cocountable sets have complements that are countable, meaning their non-elements form a set with finite or countably infinite size, while coinfinite sets have complements that are infinite but not necessarily countable. The key difference lies in the nature of their complements: cocountable complements are strictly countable, whereas coinfinite complements are infinite without countability constraints. This distinction affects how these sets behave in measure theory and topology, particularly in contexts involving sigma-algebras and Borel sets.
Mathematical Formalism and Notation
In measure theory, a subset \(A\) of a set \(X\) equipped with a s-algebra is cocountable if its complement \(X \setminus A\) is countable, often denoted as \(X \setminus A \in \mathrm{Countable}\). Coinfinite sets, defined by having a finite complement, satisfy \(X \setminus A \in \mathrm{Finite}\), positioning them as a stronger condition within the hierarchy of small sets. These concepts formalize negligible subsets in topological and measure-theoretic contexts, emphasizing the role of complement cardinality in defining cocountability and coinfiniteness.
Examples of Cocountable Sets
Cocountable sets are those whose complements are countable, such as the set of all real numbers except for a countable subset like the rationals or algebraic numbers. For example, the set of irrational numbers is cocountable because its complement, the rationals, is countable. In contrast, co-infinite sets only require their complements to be finite, so all cocountable sets are co-infinite but not all co-infinite sets are cocountable.
Examples of Coinfinite Sets
Examples of coinfinite sets include the set of prime numbers and the set of odd numbers within the natural numbers; both are infinite, yet their complements--the non-prime numbers and even numbers--are also infinite. Another example is the set of irrational numbers, whose complement, the rational numbers, is infinite as well, highlighting the coinfinite property. These examples illustrate how coinfinite sets and their complements maintain infinite cardinality simultaneously.
Applications in Topology and Analysis
Cocountable and coinfinite sets play critical roles in topology and analysis by influencing the structure of topological spaces and measurable functions. Cocountable sets, whose complements are countable, often generate cocountable topologies that are used to study convergence, continuity, and separability properties, especially in non-Hausdorff spaces. Coinfinite sets, with finite complements, are essential in defining cofinite topologies that simplify compactness and connectedness discussions, supporting applications such as function spaces and cardinal invariants in analysis.
Common Misconceptions and Pitfalls
Cocountable sets are those whose complements in a given universe are countable, whereas coinfinite sets have complements that are infinite but not necessarily countable. A common misconception is treating cocountable and coinfinite sets as interchangeable, ignoring the crucial difference that cocountable implies a complement with cardinality equal to that of the natural numbers, while coinfinite only requires an infinite complement, which may be uncountable. This misunderstanding can lead to errors in proofs involving set cardinality, measure theory, or topology where precise characterization of the complement's size is essential.
Summary and Further Reading
Cocountable sets are subsets of an infinite set whose complements are countable, whereas coinfinite sets have complements that are infinite but not necessarily countable. This distinction is critical in measure theory, topology, and infinite combinatorics for understanding set properties related to infinity and cardinality. For further reading, consult advanced texts in set theory such as *Set Theory* by Thomas Jech and research articles on descriptive set theory.
Cocountable Infographic
 libterm.com
libterm.com