A diffeomorphism is a smooth, invertible function between differentiable manifolds that preserves their structure, ensuring both the function and its inverse are continuously differentiable. This concept is fundamental in differential geometry and plays a critical role in understanding the topology and geometry of smooth shapes. Explore the rest of the article to uncover how diffeomorphisms impact modern mathematical and physical theories.
Table of Comparison
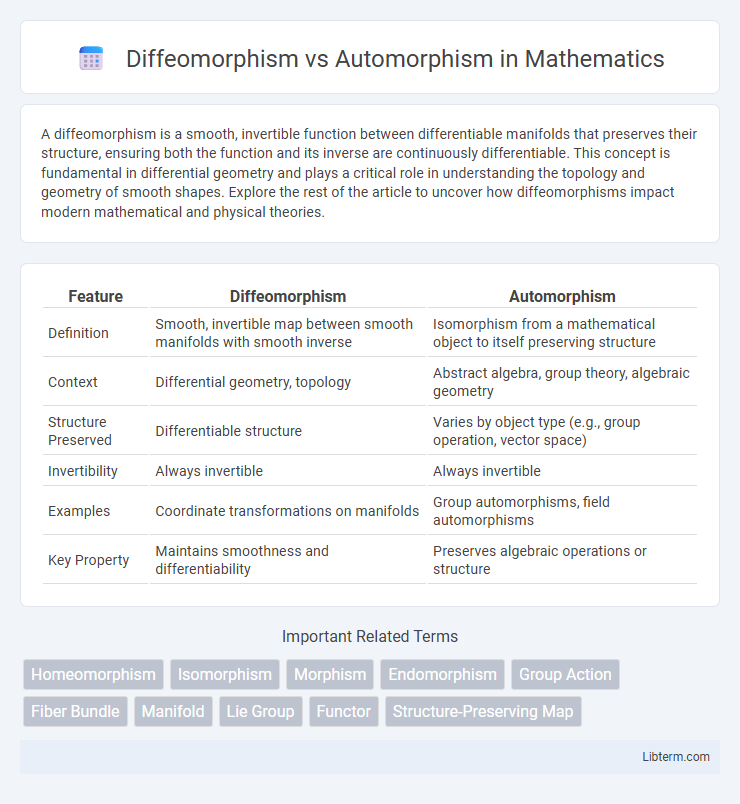
| Feature | Diffeomorphism | Automorphism |
|---|---|---|
| Definition | Smooth, invertible map between smooth manifolds with smooth inverse | Isomorphism from a mathematical object to itself preserving structure |
| Context | Differential geometry, topology | Abstract algebra, group theory, algebraic geometry |
| Structure Preserved | Differentiable structure | Varies by object type (e.g., group operation, vector space) |
| Invertibility | Always invertible | Always invertible |
| Examples | Coordinate transformations on manifolds | Group automorphisms, field automorphisms |
| Key Property | Maintains smoothness and differentiability | Preserves algebraic operations or structure |
Introduction to Diffeomorphism and Automorphism
Diffeomorphisms are smooth, invertible maps between differentiable manifolds that preserve the manifold structure, making them fundamental in differential geometry and topology. Automorphisms are structure-preserving isomorphisms from a mathematical object to itself, often studied in fields such as algebra, geometry, and category theory, representing symmetries within the object. Understanding diffeomorphisms provides insight into smooth manifold transformations, while automorphisms reveal intrinsic symmetries of abstract mathematical entities.
Mathematical Definitions and Concepts
A diffeomorphism is a smooth, invertible function between differentiable manifolds with a smooth inverse, preserving the manifold's differentiable structure. An automorphism in mathematics refers to a structure-preserving isomorphism from an object to itself, often within algebraic contexts such as groups, rings, or vector spaces. While diffeomorphisms specifically concern smooth manifolds and their geometric properties, automorphisms address symmetries and invariants within abstract algebraic or geometric structures.
Key Differences at a Glance
Diffeomorphism refers to a smooth, invertible map between differentiable manifolds preserving smooth structure, while automorphism is an isomorphism from a mathematical object to itself, preserving its defined structure. Key differences include that diffeomorphisms require differentiability and invertibility in the category of manifolds, whereas automorphisms apply more generally to algebraic, geometric, or topological structures without necessarily involving smoothness. The scope of automorphisms extends beyond manifolds to groups, rings, or vector spaces, making diffeomorphisms a specialized subset focused on differential geometry.
Geometric Perspective: Diffeomorphism Explained
Diffeomorphisms are smooth, invertible maps between differentiable manifolds that preserve the geometric structure by ensuring differentiability of both the map and its inverse. They play a central role in differential geometry by enabling the comparison of manifold structures through smooth transformations, contrasting with automorphisms which are structure-preserving maps within a single mathematical object, such as groups or vector spaces. Understanding diffeomorphisms facilitates insights into manifold equivalence, smooth deformations, and the intrinsic geometry of spaces beyond mere topological properties.
Algebraic Perspective: Understanding Automorphism
Automorphisms in algebra represent structure-preserving isomorphisms from an algebraic object to itself, maintaining operations like addition and multiplication within groups, rings, or fields. Diffeomorphisms, while conceptually related as isomorphisms in differential geometry, operate on smooth manifolds preserving differentiable structure rather than algebraic operations. Understanding automorphisms through an algebraic lens highlights their role in symmetries and invariants of algebraic structures, facilitating the study of group actions, field extensions, and ring homomorphisms.
Applications in Mathematics and Physics
Diffeomorphisms serve as smooth, invertible mappings between manifolds, crucial in differential geometry for understanding the structure-preserving transformations of smooth spaces, and they enable concepts such as curvature and geodesics in general relativity. Automorphisms act as structure-preserving isomorphisms within algebraic systems like groups, rings, and fields, essential in algebraic topology and quantum mechanics for preserving symmetry and invariants. Both concepts underpin key applications: diffeomorphisms characterize spacetime manifolds in physics, while automorphisms classify symmetries in mathematical systems and physical theories, facilitating model equivalences and conservation laws.
Examples in Manifolds and Group Theory
Diffeomorphisms are smooth bijections between manifolds that have smooth inverses, such as the map from a 2-sphere to itself rotating points by a fixed angle, preserving the manifold's differentiable structure. Automorphisms in group theory refer to isomorphisms from a group to itself, such as the conjugation map in a group or the identity automorphism preserving group operations. While diffeomorphisms focus on smooth structure preservation in manifolds, automorphisms emphasize algebraic structure invariance within groups, highlighting their roles in topology versus abstract algebra.
Importance in Topology and Structure Preservation
Diffeomorphisms are smooth, invertible maps between manifolds that preserve differentiable structure, playing a crucial role in differential topology by enabling the classification of manifolds up to smooth equivalence. Automorphisms, as isomorphisms of algebraic structures or topological spaces onto themselves, preserve the intrinsic structure, such as group operations or topological properties, essential in studying symmetry and invariants within topology. Both concepts facilitate understanding of structure preservation, with diffeomorphisms focusing on smooth manifolds and automorphisms encompassing a broader context of algebraic and topological structures.
Similarities and Overlapping Concepts
Diffeomorphisms and automorphisms both represent structure-preserving maps in mathematics, where diffeomorphisms are smooth bijections with smooth inverses between manifolds and automorphisms are isomorphisms from a mathematical object to itself preserving its structure, such as groups, rings, or vector spaces. Both concepts emphasize invertibility and preservation of underlying structures, embedding the idea of symmetry and equivalence within geometric or algebraic contexts. The overlapping idea lies in their role as transformations that maintain inherent properties, enabling analysis of invariants and facilitating classification of mathematical objects.
Summary and Implications for Advanced Study
Diffeomorphism refers to a smooth, invertible map between manifolds preserving differentiable structure, while automorphism denotes an isomorphism within algebraic or geometric structures maintaining internal consistency. Understanding the distinction enables advanced study in differential geometry and topology, where diffeomorphisms classify manifold equivalences and automorphisms characterize symmetry groups. Research implications include exploring moduli spaces, deformation theory, and complex manifold invariants through the interplay of these transformations.
Diffeomorphism Infographic
 libterm.com
libterm.com