Sheaf cohomology provides a powerful tool in algebraic geometry and topology for systematically analyzing the global properties of geometric spaces through local data. By assigning algebraic invariants to sheaves, it captures essential structural information that aids in solving complex mathematical problems related to continuity, divisors, and bundles. Explore this article to deepen your understanding of how sheaf cohomology bridges local and global aspects in modern mathematical research.
Table of Comparison
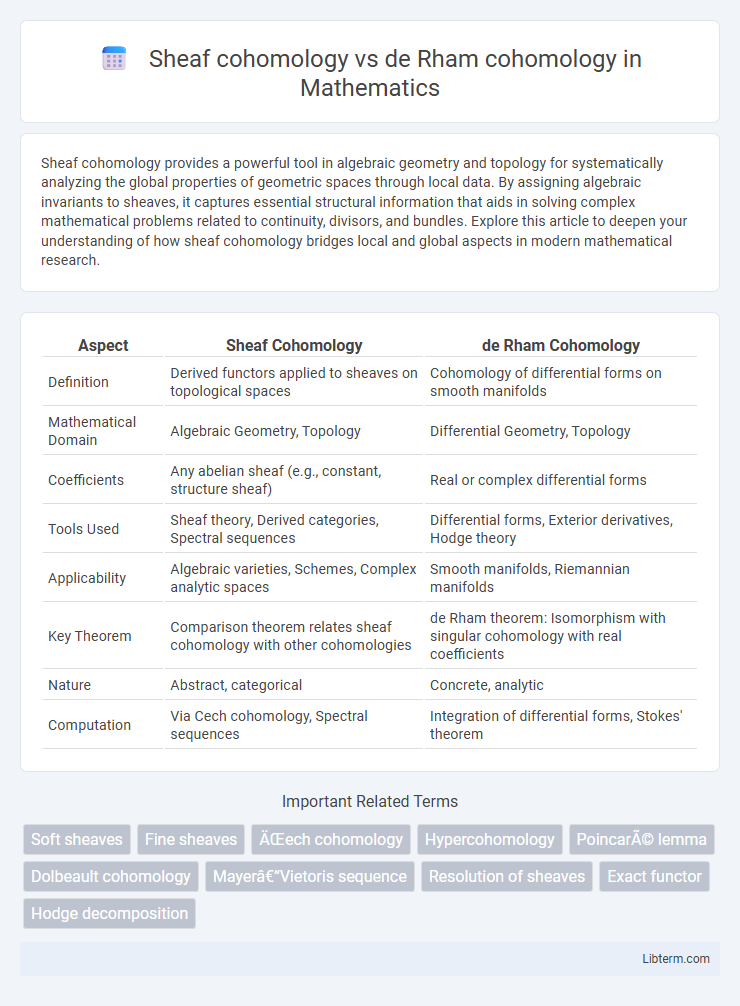
| Aspect | Sheaf Cohomology | de Rham Cohomology |
|---|---|---|
| Definition | Derived functors applied to sheaves on topological spaces | Cohomology of differential forms on smooth manifolds |
| Mathematical Domain | Algebraic Geometry, Topology | Differential Geometry, Topology |
| Coefficients | Any abelian sheaf (e.g., constant, structure sheaf) | Real or complex differential forms |
| Tools Used | Sheaf theory, Derived categories, Spectral sequences | Differential forms, Exterior derivatives, Hodge theory |
| Applicability | Algebraic varieties, Schemes, Complex analytic spaces | Smooth manifolds, Riemannian manifolds |
| Key Theorem | Comparison theorem relates sheaf cohomology with other cohomologies | de Rham theorem: Isomorphism with singular cohomology with real coefficients |
| Nature | Abstract, categorical | Concrete, analytic |
| Computation | Via Cech cohomology, Spectral sequences | Integration of differential forms, Stokes' theorem |
Introduction to Sheaf Cohomology and de Rham Cohomology
Sheaf cohomology provides a systematic framework to analyze global sections of sheaves and capture topological and algebraic information of spaces, especially in algebraic geometry and complex manifolds. De Rham cohomology, constructed from differential forms on smooth manifolds, measures the failure of exactness in the de Rham complex and offers topological invariants related to differentiable structures. Both theories establish powerful connections between local data and global topological properties, with sheaf cohomology generalizing the notion of cohomology while de Rham cohomology specifically leverages smooth differential forms.
Fundamental Concepts and Definitions
Sheaf cohomology is a powerful tool in algebraic geometry and topology that systematically studies the global sections of a sheaf, capturing information about local-to-global extensions and obstructions. De Rham cohomology, defined using differential forms on smooth manifolds, computes topological invariants by analyzing closed and exact forms through exterior derivatives. Both cohomologies reveal deep connections between algebraic and analytic structures, with sheaf cohomology generalizing the notion of functions and sections, while de Rham cohomology provides a differential-geometric perspective on manifold topology.
Historical Development and Motivation
Sheaf cohomology emerged in the mid-20th century as a tool to generalize various cohomology theories for topological spaces, particularly driven by Henri Cartan and Jean-Pierre Serre's work on complex analytic spaces. De Rham cohomology, introduced by Georges de Rham in the 1930s, provided a bridge between differential forms and topology by identifying topological invariants of smooth manifolds through differential calculus. The motivation behind sheaf cohomology was to systematically study global properties of spaces using local data encoded in sheaves, extending de Rham's ideas beyond differentiable manifolds to more general settings.
Sheaf Cohomology: Structure and Methods
Sheaf cohomology systematically encodes global information about topological spaces by analyzing sheaves, which assign algebraic data to open sets with compatibility conditions. This method leverages derived functors and injective resolutions to compute cohomology groups, translating complex geometric problems into algebraic terms. Compared to de Rham cohomology, which uses differential forms and focuses on smooth manifolds, sheaf cohomology applies more broadly to various topological and algebraic settings.
de Rham Cohomology: Differential Forms Approach
De Rham cohomology uses differential forms to analyze topological properties of manifolds by computing cohomology groups derived from the exterior derivative operator. This approach translates geometric problems into algebraic ones by studying closed and exact differential forms, revealing global invariants like Betti numbers. The de Rham theorem establishes an isomorphism between de Rham cohomology and singular cohomology with real coefficients, highlighting its key role in differential topology.
Similarities Between Sheaf and de Rham Cohomology
Sheaf cohomology and de Rham cohomology both provide tools for studying the global topological and analytical properties of smooth manifolds using local data, with sheaf cohomology generalizing the concept to arbitrary sheaves while de Rham cohomology specifically uses differential forms. Both theories yield isomorphic cohomology groups on smooth manifolds, as established by de Rham's theorem, linking algebraic topology with differential geometry through the correspondence between closed differential forms and cocycles in sheaf cohomology. They also share the property of being derived functors, interpreting global sections and closed forms as cohomological invariants capturing obstructions to local-to-global extensions.
Key Differences and Theoretical Distinctions
Sheaf cohomology provides a general framework for computing cohomological invariants of topological spaces using sheaves, capturing local-to-global properties through derived functors, whereas de Rham cohomology specifically analyzes smooth manifolds via differential forms and exterior derivatives. Key differences include sheaf cohomology's applicability to broader categories of spaces and coefficients beyond differential forms, while de Rham cohomology relies heavily on smooth structure and integration theory. Theoretical distinctions arise as de Rham cohomology is isomorphic to singular cohomology with real coefficients on smooth manifolds, whereas sheaf cohomology encompasses a more abstract approach applicable to various cohomology theories across algebraic geometry and complex analysis.
Applications in Algebraic and Differential Geometry
Sheaf cohomology provides powerful tools for studying algebraic varieties by encoding local-to-global properties of sheaves, crucial for classifying line bundles and understanding divisor theory. De Rham cohomology captures the differential structure of smooth manifolds through differential forms, enabling the computation of topological invariants like Betti numbers and facilitating Hodge theory. Both cohomology theories intersect in complex geometry, where sheaf cohomology of holomorphic forms aligns with de Rham cohomology, thus bridging algebraic and differential geometric frameworks.
Comparative Examples and Computations
Sheaf cohomology and de Rham cohomology both provide tools for analyzing the topological and geometric structures of manifolds, with sheaf cohomology utilizing the derived functors of global section functors on sheaves, while de Rham cohomology uses differential forms and the exterior derivative. For example, on a smooth manifold, de Rham's theorem states the isomorphism \(H^k_{dR}(M) \cong H^k(M, \mathbb{R})\), linking de Rham cohomology groups to sheaf cohomology groups of locally constant sheaves. In computations, sheaf cohomology often utilizes Cech cohomology or injective resolutions for coherent sheaves, whereas de Rham cohomology typically involves integrating differential forms over cycles and solving \(\mathrm{d}\omega = 0\) and \(\omega = \mathrm{d}\eta\) conditions on forms.
Conclusion: Choosing the Appropriate Cohomology Tool
Sheaf cohomology provides a flexible framework suited for analyzing global sections of sheaves in complex algebraic varieties, making it essential for problems involving local-to-global principles. De Rham cohomology is specifically valuable for smooth manifolds, capturing differential forms and topological invariants tied to real-valued functions. Selecting between sheaf and de Rham cohomology depends on the geometric context and the algebraic or analytical nature of the problem, with sheaf cohomology excelling in algebraic geometry and de Rham cohomology in differential topology.
Sheaf cohomology Infographic
 libterm.com
libterm.com