Topological spaces provide a fundamental framework in mathematics for understanding continuity, convergence, and boundary concepts without relying on specific distances. By defining open sets and neighborhoods, they allow the study of spatial properties that remain invariant under continuous transformations. Explore the rest of this article to deepen your understanding of how topological spaces shape various fields of science and mathematics.
Table of Comparison
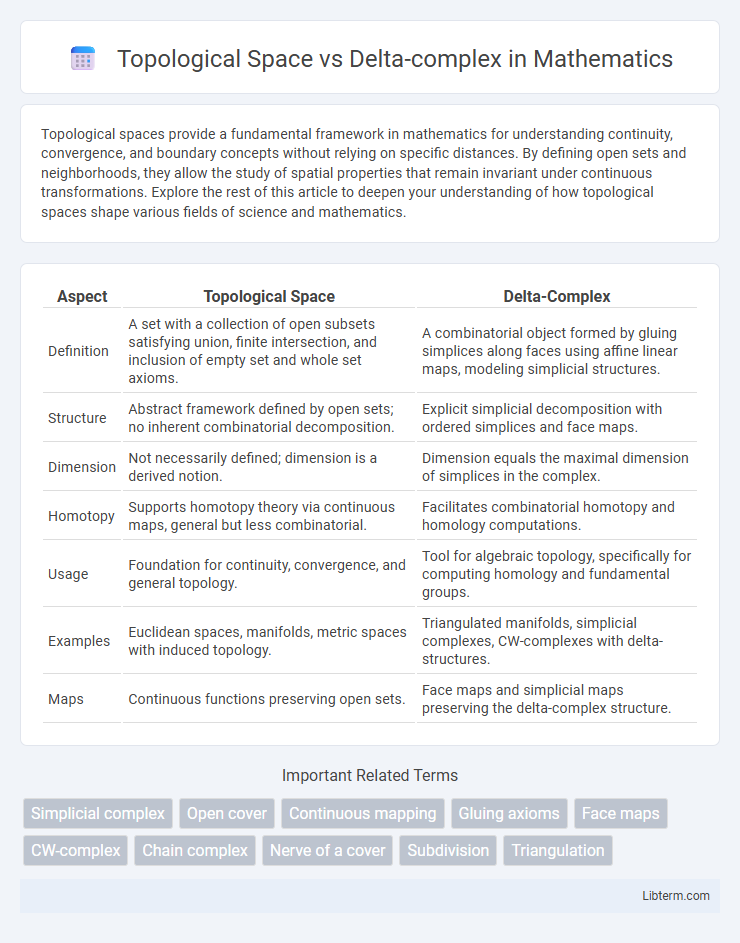
| Aspect | Topological Space | Delta-Complex |
|---|---|---|
| Definition | A set with a collection of open subsets satisfying union, finite intersection, and inclusion of empty set and whole set axioms. | A combinatorial object formed by gluing simplices along faces using affine linear maps, modeling simplicial structures. |
| Structure | Abstract framework defined by open sets; no inherent combinatorial decomposition. | Explicit simplicial decomposition with ordered simplices and face maps. |
| Dimension | Not necessarily defined; dimension is a derived notion. | Dimension equals the maximal dimension of simplices in the complex. |
| Homotopy | Supports homotopy theory via continuous maps, general but less combinatorial. | Facilitates combinatorial homotopy and homology computations. |
| Usage | Foundation for continuity, convergence, and general topology. | Tool for algebraic topology, specifically for computing homology and fundamental groups. |
| Examples | Euclidean spaces, manifolds, metric spaces with induced topology. | Triangulated manifolds, simplicial complexes, CW-complexes with delta-structures. |
| Maps | Continuous functions preserving open sets. | Face maps and simplicial maps preserving the delta-complex structure. |
Introduction to Topological Spaces and Delta-complexes
Topological spaces provide a fundamental framework in mathematics defined by a set equipped with a collection of open subsets satisfying specific axioms, enabling the study of continuity, convergence, and connectedness. Delta-complexes, a generalization of simplicial complexes, structure spaces using simplices glued together along their faces, facilitating combinatorial and algebraic topology analyses. Understanding the differences between general topological spaces and the combinatorial nature of delta-complexes aids in exploring homotopy, homology, and geometric properties in topology.
Fundamental Definitions and Key Concepts
A topological space is defined by a set equipped with a collection of open sets satisfying union, finite intersection, and inclusion of the set itself and the empty set, forming the basis for concepts like continuity, convergence, and connectedness. A Delta-complex is a combinatorial structure built from simplices glued together along faces in a way that generalizes simplicial complexes, providing a framework to study homology and the fundamental group via explicit cell attachments. While topological spaces offer a broad, abstract framework, Delta-complexes enable concrete algebraic and geometric computations essential in algebraic topology.
Structure of Topological Spaces
Topological spaces consist of a set equipped with a topology, a collection of open sets that satisfy union, intersection, and inclusion axioms, providing a framework for continuity and convergence. Delta-complexes are combinatorial structures built from simplices glued together along faces, inducing a specific topology but emphasizing geometric and algebraic properties for homology computations. The structure of topological spaces is more general and flexible, enabling a wide range of continuous transformations, while delta-complexes impose a triangulated framework that facilitates explicit calculations in algebraic topology.
Core Properties of Delta-complexes
Delta-complexes provide a combinatorial framework that captures the essential features of topological spaces through simplicial structures, allowing for efficient computations in algebraic topology. Core properties include the ability to decompose spaces into simplices glued together along faces, preserving homotopy type and facilitating homology calculations. This structured approach contrasts with general topological spaces by emphasizing simplicial attachments and face identifications, optimizing analysis via chain complexes and boundary operators.
Construction Methods: Topological Spaces vs Delta-complexes
Topological spaces are constructed by defining open sets that satisfy the axioms of topology, allowing for a broad and flexible framework for continuity and convergence. Delta-complexes are built using simplices glued together via face maps, providing a combinatorial and algebraic approach to studying topological spaces. This construction method enables explicit computation of homology groups through simplicial chains, streamlining algebraic topology applications.
Examples Illustrating Each Concept
A topological space example is the Euclidean space \(\mathbb{R}^n\) with open sets defined by open balls, showcasing general continuity and convergence properties. In contrast, a delta-complex example is the 2-simplex formed by gluing together triangles along edges, used to study combinatorial structures and homology groups. These distinctions highlight how topological spaces provide broad frameworks for discussing open sets, while delta-complexes emphasize discrete simplices and their combinatorial connections.
Comparative Analysis: Similarities and Differences
Topological spaces and Delta-complexes both provide frameworks for studying spatial structures, with topological spaces emphasizing open sets and continuity, while Delta-complexes focus on simplicial decompositions using simplices and face identifications. Both concepts facilitate the analysis of connectivity and homotopy properties, but Delta-complexes offer a combinatorial approach enabling explicit calculations of homology and cohomology groups. Key differences arise in their construction: topological spaces are general and flexible, accommodating various topologies, whereas Delta-complexes are more rigid, defined by a finite set of simplices assembled via face maps.
Applications in Algebraic Topology
Topological spaces provide the foundational framework for defining continuous functions and general topological properties essential in algebraic topology. Delta-complexes offer a combinatorial approach to studying homotopy and homology, enabling explicit calculations of algebraic invariants like singular homology groups and homotopy groups. These structures facilitate complex constructions such as CW complexes, which are pivotal in classifying spaces via algebraic invariants and simplifying computational topology problems.
Advantages and Limitations
Delta-complexes provide a combinatorial approach to topological spaces, enabling explicit calculations of homology groups through simplicial structures that simplify computational complexity. Topological spaces offer greater generality and flexibility, accommodating broader classes of spaces beyond simplicial decompositions but often complicate direct algebraic or combinatorial analysis. While delta-complexes are advantageous for discrete geometric intuition and algorithmic implementation, their limitation lies in reduced applicability to non-simplicial or pathological spaces intrinsic to general topology.
Summary and Future Directions
Topological spaces provide a broad framework characterized by open sets defining continuity and convergence, whereas delta-complexes offer a combinatorial structure ideal for computational topology and homology calculations. Future directions include enhancing algorithmic methods for delta-complex decomposition to improve efficiency in persistent homology and expanding applications in high-dimensional data analysis. Integration of topological data analysis with machine learning promises significant advancements in the study of complex datasets using both topological spaces and delta-complex frameworks.
Topological Space Infographic
 libterm.com
libterm.com