Inductive limit is a fundamental concept in category theory and algebra that describes the process of constructing a new object by coherently combining a directed system of objects and morphisms. This method allows you to analyze complex structures by understanding their simpler components and the ways they interact within the system. Explore the article to uncover detailed explanations and practical applications of inductive limits.
Table of Comparison
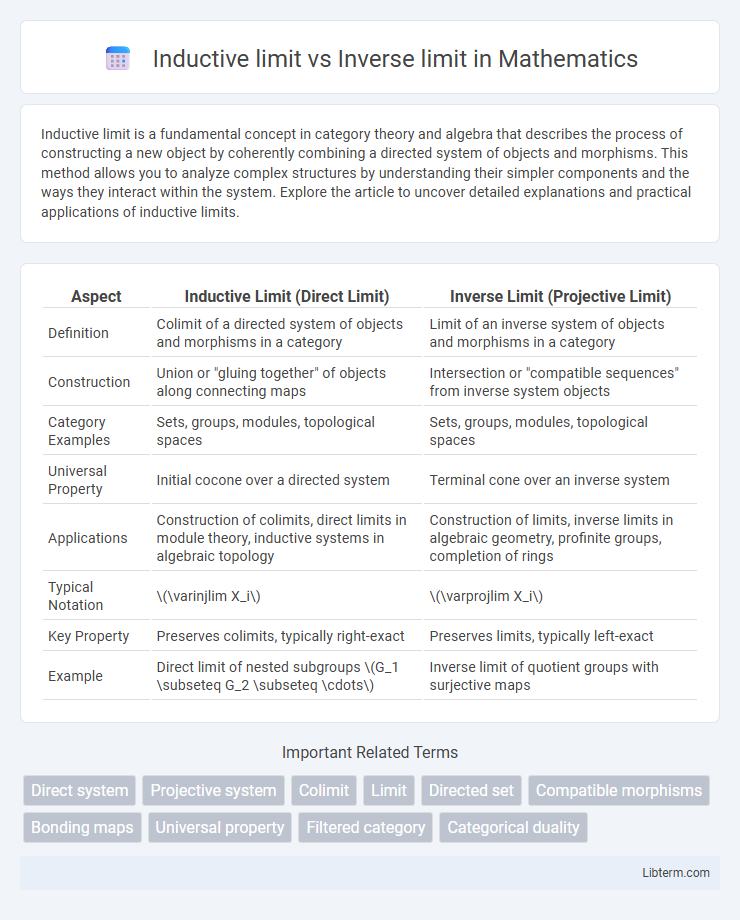
| Aspect | Inductive Limit (Direct Limit) | Inverse Limit (Projective Limit) |
|---|---|---|
| Definition | Colimit of a directed system of objects and morphisms in a category | Limit of an inverse system of objects and morphisms in a category |
| Construction | Union or "gluing together" of objects along connecting maps | Intersection or "compatible sequences" from inverse system objects |
| Category Examples | Sets, groups, modules, topological spaces | Sets, groups, modules, topological spaces |
| Universal Property | Initial cocone over a directed system | Terminal cone over an inverse system |
| Applications | Construction of colimits, direct limits in module theory, inductive systems in algebraic topology | Construction of limits, inverse limits in algebraic geometry, profinite groups, completion of rings |
| Typical Notation | \(\varinjlim X_i\) | \(\varprojlim X_i\) |
| Key Property | Preserves colimits, typically right-exact | Preserves limits, typically left-exact |
| Example | Direct limit of nested subgroups \(G_1 \subseteq G_2 \subseteq \cdots\) | Inverse limit of quotient groups with surjective maps |
Introduction to Inductive and Inverse Limits
Inductive limits, also known as direct limits, systematically combine objects and morphisms in a directed system, capturing the "union" or colimit in categories such as sets, groups, or topological spaces. Inverse limits, or projective limits, assemble objects and morphisms from an inverse system, producing a universal object representing the "intersection" or limit, crucial in algebraic topology, analysis, and algebra. Understanding the distinctions between inductive and inverse limits is fundamental for studying the behavior of sequences of structures and their convergence properties in category theory.
Defining Inductive (Direct) Limits
Inductive (direct) limits are constructed in category theory to capture the colimit of a directed system of objects and morphisms indexed by a directed partially ordered set, allowing the assembly of an object that coherently unifies the entire system. This concept contrasts with inverse limits, which focus on limits of inverse systems characterized by projective properties, highlighting the duality in categorical constructions. Inductive limits are fundamental in algebra and topology for building large structures from local data, playing a critical role in modules, sheaves, and topological spaces.
Understanding Inverse (Projective) Limits
Inverse limits, also known as projective limits, provide a method to construct a new object as a limit of an inverse system of spaces or algebraic structures connected by bonding maps. These limits capture the idea of consistently "gluing together" objects along compatible projections, often used in topology, algebra, and category theory to study properties preserved under inverse systems. Understanding inverse limits enables deep analysis of complex spaces by decomposing them into simpler approximations, revealing structural and continuity aspects not evident in individual components.
Key Differences Between Inductive and Inverse Limits
Inductive limits, also known as direct limits, construct a universal object by coherently aggregating an increasing sequence of spaces or structures with compatible morphisms, emphasizing colimits in categories. Inverse limits, or projective limits, form a universal object by taking consistent tuples from a decreasing sequence of spaces or structures linked by morphisms, focusing on limits in categories. The key difference lies in inductive limits capturing the union and directed colimit behavior, while inverse limits emphasize intersections and projective limit properties, reflecting dual categorical concepts.
Examples of Inductive Limits in Mathematics
Inductive limits in mathematics often arise in algebraic topology and functional analysis, such as the construction of the direct limit of a sequence of groups or vector spaces, where each group maps into the next one via homomorphisms. A classical example is the colimit of an ascending chain of abelian groups \( G_1 \subseteq G_2 \subseteq \cdots \), which captures the union of these groups with consistent structure. Another significant instance appears in the theory of \( C^* \)-algebras, where inductive limits are used to build more complex algebras from simpler building blocks, allowing the study of infinite-dimensional phenomena.
Illustrative Cases of Inverse Limits
Inverse limits capture the essence of constructing objects from an infinite sequence of approximations connected by projection maps, often visualized in topological or algebraic contexts such as the Cantor set arising as an inverse limit of finite discrete spaces. Illustrative cases include the construction of profinite groups by taking inverse limits of finite groups, revealing deep connections between algebraic properties and topological compactness. These examples highlight inverse limits as powerful tools for synthesizing complex structures from simpler building blocks, contrasting with inductive limits that focus on colimits or unions of directed systems.
Applications of Inductive vs Inverse Limits
Inductive limits are extensively used in algebraic topology and functional analysis to construct large objects from directed systems of smaller spaces, such as building CW-complexes or direct limits of modules. Inverse limits find critical applications in number theory, algebraic geometry, and topology for defining profinite groups, completions of rings, and spectral sequences. The choice between inductive and inverse limits depends on whether the goal is to unify data from expanding structures or to capture consistent information from refining approximations.
Properties and Theorems Involving Limits
Inductive limits, also known as direct limits, preserve colimits in diagram categories, ensuring universality with respect to morphisms from the system, while inverse limits or projective limits preserve limits such as products and equalizers, maintaining universality in relation to morphisms into the system. The Mittag-Leffler condition provides criteria for the exactness of inverse limits in abelian categories, and the independence of inductive limits from the choice of the indexing category under filteredness is a fundamental property in category theory. Key theorems like the Adjoint Functor Theorem ensure the existence of these limits under completeness or cocompleteness, highlighting their essential role in algebra, topology, and functional analysis.
Common Mistakes and Misconceptions
Many confuse inductive limits with inverse limits by assuming their constructions and applications are interchangeable, overlooking that inductive limits build objects from directed systems via colimits, while inverse limits form objects through projective systems using limits. Another common mistake is neglecting the distinct topological or categorical contexts where each limit applies, leading to incorrect generalizations about continuity or convergence properties. Misunderstandings also arise from treating morphisms in these limits identically, ignoring that inductive limits use transition maps compatible with direct systems, whereas inverse limits depend on bonding maps in inverse systems, affecting their respective universal properties.
Conclusion: Choosing the Right Limit for Your Context
Inductive limits are optimal for constructing objects by unifying an ascending sequence of structures, making them ideal in algebraic topology and category theory when dealing with colimits. Inverse limits excel at capturing projective systems' behavior through consistent projections, commonly used in number theory and algebraic geometry. Selecting between inductive and inverse limits depends on whether the context emphasizes building up through inclusions or refining down through projections to ensure coherent structure integration.
Inductive limit Infographic
 libterm.com
libterm.com