A singleton set is a set containing exactly one element, making it a fundamental concept in set theory and mathematics. This simple structure plays a crucial role in defining functions, topologies, and in various proofs where unique identification is necessary. Explore the rest of the article to understand how singleton sets impact your mathematical reasoning and applications.
Table of Comparison
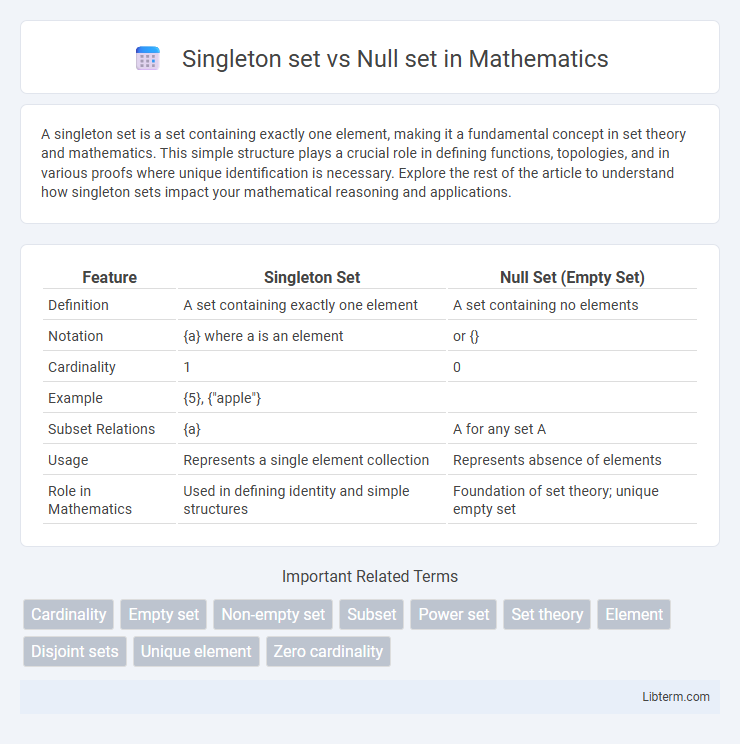
| Feature | Singleton Set | Null Set (Empty Set) |
|---|---|---|
| Definition | A set containing exactly one element | A set containing no elements |
| Notation | {a} where a is an element | or {} |
| Cardinality | 1 | 0 |
| Example | {5}, {"apple"} | |
| Subset Relations | {a} | A for any set A |
| Usage | Represents a single element collection | Represents absence of elements |
| Role in Mathematics | Used in defining identity and simple structures | Foundation of set theory; unique empty set |
Definition of Singleton Set
A singleton set is a set containing exactly one element, represented as {a} where 'a' is that single element. In contrast, a null set, also known as an empty set, contains no elements and is denoted by . The defining characteristic of a singleton set is its unique single member, differentiating it clearly from the null set.
Definition of Null Set
A null set, also known as an empty set, is a set that contains no elements, represented by or {}. In contrast, a singleton set has exactly one element, such as {a}. The null set serves as the foundational concept in set theory, highlighting the absence of any member within the set.
Symbolic Representation
The singleton set is symbolically represented as {a}, containing exactly one element "a", whereas the null set is represented by the symbol or {} indicating it contains no elements. In set theory, the distinction between {a} and is crucial for understanding membership and subset relations. The symbolic difference highlights that {a} , emphasizing the presence of one element in the singleton set and none in the null set.
Cardinality Comparison
A singleton set contains exactly one element, so its cardinality is 1, whereas a null set or empty set contains no elements, giving it a cardinality of 0. The cardinality comparison between these sets highlights that the singleton set is strictly larger in terms of size or element count. This distinction is fundamental in set theory, where the null set is unique with zero elements and the singleton set serves as the simplest non-empty set.
Examples of Singleton Sets
A singleton set contains exactly one element, such as {5} or {"apple"}, representing a set with a single unique member. In contrast, a null set, also called an empty set, contains no elements and is denoted by {} or . Examples of singleton sets include {0}, which contains only the number zero, and {p}, containing only the mathematical constant pi.
Examples of Null Sets
A null set, also known as an empty set, contains no elements, represented as {} or , while a singleton set consists of exactly one element, such as {5}. Examples of null sets include the set of natural numbers less than zero and the set of solutions to x^2 + 1 = 0 over real numbers. Recognizing null sets is essential in set theory and mathematical proofs to distinguish them from sets with elements, including singleton sets.
Key Differences Between Singleton and Null Sets
A singleton set contains exactly one element, making its cardinality equal to one, whereas a null set, also known as an empty set, contains no elements and has a cardinality of zero. The singleton set is non-empty and can be represented as {a}, where 'a' is any element, while the null set is denoted by or {} and serves as the identity element for union operations in set theory. Key differences include their cardinality, element presence, and roles in operations like union and intersection within mathematical contexts.
Role in Set Theory
A singleton set contains exactly one element, serving as a fundamental building block for constructing and analyzing more complex sets in set theory, while a null set, or empty set, contains no elements and acts as the unique identity element for the operation of union. Singleton sets are crucial in defining functions, sequences, and relations due to their precise cardinality of one, whereas the null set establishes the baseline concept of "nothingness" and is essential for defining subsets and bases for inductive proofs. Both sets play complementary roles in axiomatic set theory, with the null set ensuring consistency by representing the minimal set and singleton sets facilitating the creation of atomic units in set construction.
Applications in Mathematics
A singleton set, containing exactly one element, is fundamental in defining identity elements and unit structures in algebraic systems, while a null set, or empty set, serves as the essential foundation of set theory and is critical for proving base cases in mathematical induction. Singleton sets enable precise characterization of functions, such as characteristic functions and equivalence classes, whereas null sets are pivotal in measure theory and probability, representing events with zero probability. Both play distinct roles in topology, where singletons form closed sets in T1 spaces and null sets often describe empty interiors or measure-zero subsets.
Common Misconceptions
A common misconception is that a singleton set and a null set are the same due to their minimal cardinality, but the null set contains no elements while a singleton set contains exactly one element. Another misunderstanding involves treating the null set as just an empty list, ignoring its unique property as the only set with zero cardinality in set theory. Confusing these concepts can lead to errors in mathematical proofs, especially in topics like topology and measure theory where the distinction impacts outcomes significantly.
Singleton set Infographic
 libterm.com
libterm.com