Commutative algebra explores the properties and structures of commutative rings, ideals, and modules, forming the foundation for algebraic geometry and number theory. Understanding concepts such as prime ideals, localization, and Noetherian rings is essential for deepening your knowledge in modern mathematical research. Dive into the rest of the article to unlock the key principles and applications of commutative algebra.
Table of Comparison
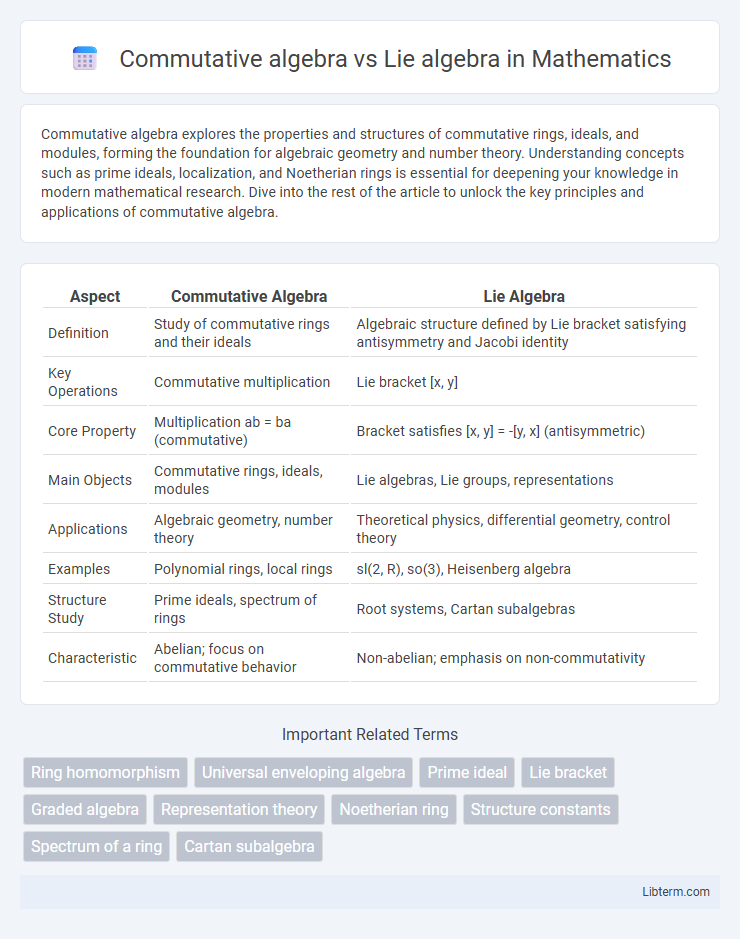
| Aspect | Commutative Algebra | Lie Algebra |
|---|---|---|
| Definition | Study of commutative rings and their ideals | Algebraic structure defined by Lie bracket satisfying antisymmetry and Jacobi identity |
| Key Operations | Commutative multiplication | Lie bracket [x, y] |
| Core Property | Multiplication ab = ba (commutative) | Bracket satisfies [x, y] = -[y, x] (antisymmetric) |
| Main Objects | Commutative rings, ideals, modules | Lie algebras, Lie groups, representations |
| Applications | Algebraic geometry, number theory | Theoretical physics, differential geometry, control theory |
| Examples | Polynomial rings, local rings | sl(2, R), so(3), Heisenberg algebra |
| Structure Study | Prime ideals, spectrum of rings | Root systems, Cartan subalgebras |
| Characteristic | Abelian; focus on commutative behavior | Non-abelian; emphasis on non-commutativity |
Introduction to Commutative and Lie Algebras
Commutative algebra focuses on the study of commutative rings, their ideals, and modules, serving as the foundation for algebraic geometry and number theory. Lie algebra investigates algebraic structures whose product, the Lie bracket, satisfies antisymmetry and the Jacobi identity, essential in studying symmetries and continuous transformation groups in physics and differential geometry. Introduction to commutative algebras emphasizes ring theory and module theory, while introduction to Lie algebras explores Lie brackets, Lie groups, and representation theory.
Fundamental Definitions and Concepts
Commutative algebra studies commutative rings, ideals, and modules, focusing on algebraic structures where multiplication is commutative, which is essential for algebraic geometry and number theory. Lie algebra involves vector spaces equipped with a Lie bracket, a bilinear, antisymmetric operation satisfying the Jacobi identity, used to analyze algebraic structures underlying continuous symmetry groups. The fundamental difference lies in commutativity and operation type: commutative algebra emphasizes commutative ring theory while Lie algebra centers on non-associative, non-commutative bracket operations capturing symmetry and infinitesimal transformations.
Key Structural Differences
Commutative algebra studies commutative rings where multiplication is abelian, emphasizing ideals and modules with a focus on algebraic geometry and number theory applications. Lie algebra concerns non-commutative algebras defined by the Lie bracket, characterized by antisymmetry and the Jacobi identity, modeling symmetries and continuous transformation groups. The key structural difference lies in the commutativity of the product: commutative algebra operates with symmetric multiplication, while Lie algebra involves a bilinear, antisymmetric operation that governs its algebraic structure and representation theory.
Operations in Commutative Algebra vs Lie Algebra
Operations in commutative algebra primarily involve commutative multiplication and addition within rings and modules, where elements commute under multiplication (ab = ba). In contrast, Lie algebra operations center around the Lie bracket--a bilinear, antisymmetric operation [x, y] that satisfies the Jacobi identity, capturing non-commutative structures. These fundamental differences in operations distinguish commutative algebras as studying commutative rings, while Lie algebras focus on algebraic structures modeling infinitesimal symmetries and non-commutative geometry.
Examples and Applications
Commutative algebra studies structures like polynomial rings and algebraic varieties, foundational in algebraic geometry and number theory, with examples including rings of integers and coordinate rings of curves. Lie algebra focuses on non-commutative algebras associated with continuous symmetry groups, exemplified by the set of all \( n \times n \) skew-symmetric matrices under the Lie bracket, playing a critical role in theoretical physics, particularly in quantum mechanics and gauge theory. Applications of commutative algebra center around solving polynomial equations and classifying algebraic structures, whereas Lie algebra is essential for understanding symmetry, conservation laws, and representation theory in modern physics and differential geometry.
Roles in Modern Mathematics
Commutative algebra provides the foundational framework for algebraic geometry and number theory, focusing on the study of commutative rings and their ideals, which is essential in understanding polynomial equations and algebraic varieties. Lie algebra plays a crucial role in differential geometry and theoretical physics, particularly in the study of continuous symmetries and the structure of Lie groups associated with transformation groups. Both fields contribute to modern mathematics by enabling the analysis of algebraic structures, with commutative algebra emphasizing static properties of rings and Lie algebra exploring dynamic symmetries in mathematical and physical systems.
Representation Theory Perspectives
Representation theory of commutative algebra primarily studies modules over commutative rings, emphasizing diagonalization and simple module classification. In contrast, Lie algebra representation theory explores linear actions of Lie algebras on vector spaces, focusing on weight spaces, root systems, and their roles in understanding symmetries. Lie algebra representations often involve infinite-dimensional modules and non-commutative structures, significantly enriching the theory compared to the generally simpler, module-based frameworks in commutative algebra.
Importance in Algebraic Geometry and Physics
Commutative algebra provides foundational tools for algebraic geometry through its study of commutative rings and ideals, enabling the understanding of algebraic varieties and their geometric properties. Lie algebra plays a crucial role in theoretical physics by describing symmetries and conserved quantities in particle physics and quantum field theory, thus linking algebraic structures to physical phenomena. Both areas offer essential frameworks: commutative algebra for modeling geometric spaces and Lie algebra for capturing symmetry and dynamics in physical systems.
Recent Developments and Research Directions
Recent developments in commutative algebra emphasize advances in homological methods, particularly the application of derived categories and homotopical techniques to investigate ring and module structures. In contrast, research in Lie algebra focuses on categorification, representation theory of infinite-dimensional Lie algebras, and connections with quantum groups and algebraic geometry. Both fields increasingly intersect via deformation theory and noncommutative algebraic geometry, fostering novel approaches to long-standing algebraic problems.
Conclusion and Future Comparisons
Commutative algebra centers on structures where multiplication is commutative, playing a pivotal role in algebraic geometry and number theory, while Lie algebra emphasizes non-commutative operations fundamental to studying symmetries in physics and differential equations. Future comparisons will likely explore their interactions through deformation theory and homological algebra, revealing deeper insights into geometric representation and quantum groups. Advancements in computational algebra systems may enhance the practical applications and further unify concepts across these algebraic domains.
Commutative algebra Infographic
 libterm.com
libterm.com