Limitations are boundaries that define the extent or scope of something, often influencing how goals are achieved or tasks are completed. Understanding your limits can enhance decision-making, improve time management, and foster realistic expectations in various aspects of life. Explore the full article to learn how recognizing and navigating limits can positively impact your personal and professional growth.
Table of Comparison
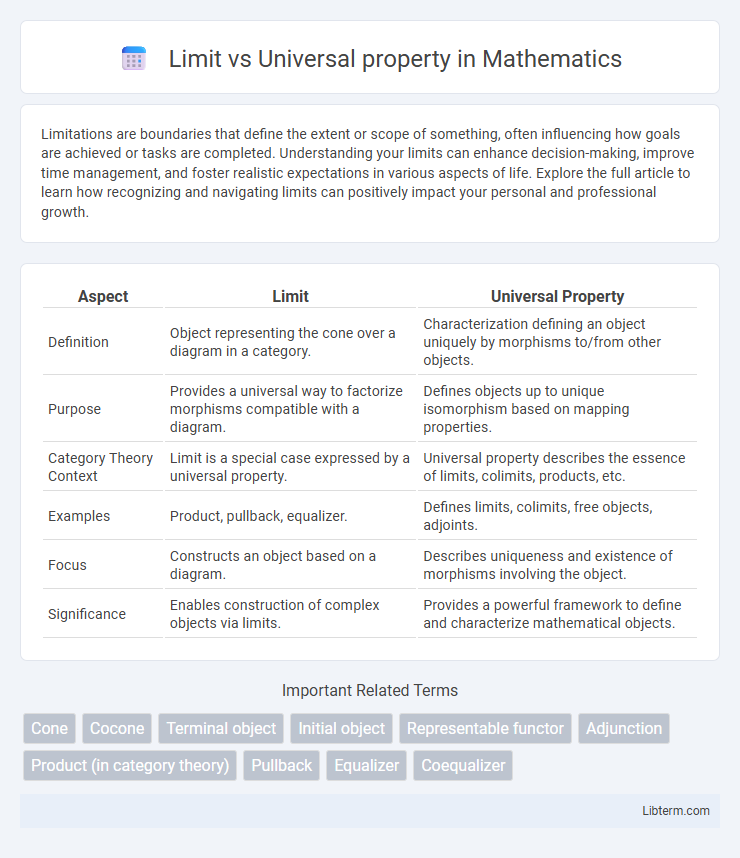
| Aspect | Limit | Universal Property |
|---|---|---|
| Definition | Object representing the cone over a diagram in a category. | Characterization defining an object uniquely by morphisms to/from other objects. |
| Purpose | Provides a universal way to factorize morphisms compatible with a diagram. | Defines objects up to unique isomorphism based on mapping properties. |
| Category Theory Context | Limit is a special case expressed by a universal property. | Universal property describes the essence of limits, colimits, products, etc. |
| Examples | Product, pullback, equalizer. | Defines limits, colimits, free objects, adjoints. |
| Focus | Constructs an object based on a diagram. | Describes uniqueness and existence of morphisms involving the object. |
| Significance | Enables construction of complex objects via limits. | Provides a powerful framework to define and characterize mathematical objects. |
Introduction to Limits and Universal Properties
Limits in category theory generalize constructions like products and pullbacks by defining an object that universally factors morphisms from a diagram, ensuring uniqueness up to isomorphism. Universal properties characterize these limits by specifying a cone that is initial among all cones to the diagram, capturing the essence of "optimality" in a categorical context. Understanding limits through universal properties enables the abstraction and unification of diverse mathematical structures, providing a foundational framework for advanced algebra and topology.
Defining Limits in Category Theory
Limits in category theory generalize constructs like products, equalizers, and pullbacks by capturing the universal property of a cone to a diagram. A limit of a diagram is an object paired with morphisms such that any other cone factors uniquely through it, ensuring uniqueness up to isomorphism. This universal property defines limits abstractly, allowing their application across diverse categories and preserving structural relationships.
Understanding Universal Properties
Universal properties characterize objects by their unique factorization properties within a category, allowing for a precise and canonical way to define constructions such as limits. Limits are examples of universal properties, serving as terminal cones that uniquely factorize morphisms from other cones, ensuring optimal and consistent mappings. Understanding universal properties provides a foundational tool for identifying and working with limits, colimits, and other categorical constructs by emphasizing their uniqueness and existence conditions.
The Relationship Between Limits and Universal Properties
Limits in category theory are characterized by their universal property, which ensures a unique morphism from any other cone to the limit object. This universal property defines the limit as the terminal object in the category of cones over a diagram, establishing a fundamental connection between the concepts. Understanding this relationship enables the construction and identification of limits through their universal mapping properties, providing a unifying framework across different categories.
Examples of Limits in Familiar Categories
In the category of sets, limits include products, equalizers, and pullbacks, where the product of sets corresponds to the Cartesian product, and equalizers select elements satisfying specific conditions. In the category of groups, the product limit constructs the direct product group, while pullbacks correspond to fibered products of groups preserving homomorphisms. These examples demonstrate how universal properties characterize limits by identifying objects and morphisms that uniquely factor through cones, ensuring consistency across diagrams in familiar algebraic and topological structures.
Universal Property as a Unifying Principle
Universal properties serve as a unifying principle in category theory by characterizing objects through their unique morphisms, encapsulating both limits and colimits in a single framework. Limits are instances of universal properties where an object represents the most general way to factor diagrams, ensuring uniqueness up to isomorphism. This abstraction simplifies proofs and constructions across mathematical disciplines by focusing on morphism-based definitions rather than elementwise arguments.
Diagrams and Cones: Visualizing Limits
Limits in category theory are best visualized through diagrams representing shapes of objects and morphisms, where cones capture the universal property by mapping consistently to all objects in the diagram. A cone consists of a vertex object and morphisms to each object in the diagram, satisfying commutativity with each arrow, embodying a universal factorization property. The limit is the universal cone through which every other cone uniquely factors, providing an abstract but powerful graphical tool to understand and prove structural properties in categories.
Common Misconceptions: Limit vs Universal Property
Limits in category theory are often misunderstood as simply universal properties, but the key distinction lies in their scope: a limit is a universal cone over a diagram, while a universal property characterizes an object uniquely up to isomorphism by mapping conditions. Many confuse limits with universal properties because every limit arises from a universal property, but not all universal properties define limits. Clarifying this distinction is fundamental for correctly applying concepts such as representable functors and adjoint functors in categorical contexts.
Applications in Mathematics and Computer Science
Limits provide a foundational framework for capturing universal constructions such as products, pullbacks, and inverse limits in category theory, which are essential in algebra, topology, and logic. Universal properties define objects uniquely up to isomorphism by characterizing their relationships through morphisms, enabling powerful abstraction and composability in functional programming, type theory, and database theory. Both concepts facilitate modular design and reasoning in computer science by representing data types, protocol specifications, and semantic domains with categorical precision.
Conclusion: The Foundational Role of Universal Properties
Universal properties serve as the foundational framework for limits by characterizing objects uniquely up to isomorphism through their universal mapping properties. This intrinsic universality enables limits to be defined and recognized across diverse categories, ensuring structural coherence and facilitating categorical constructions. Their pivotal role solidifies universal properties as central to understanding and applying limits in category theory.
Limit Infographic
 libterm.com
libterm.com