A measurable set is a fundamental concept in measure theory, defined as a set for which a measure can be consistently assigned, such as length, area, or volume. These sets play a crucial role in integrating functions and formulating probabilities, ensuring that sizes and probabilities can be quantified accurately. Explore the rest of the article to understand how measurable sets impact real-world applications and advanced mathematical theories.
Table of Comparison
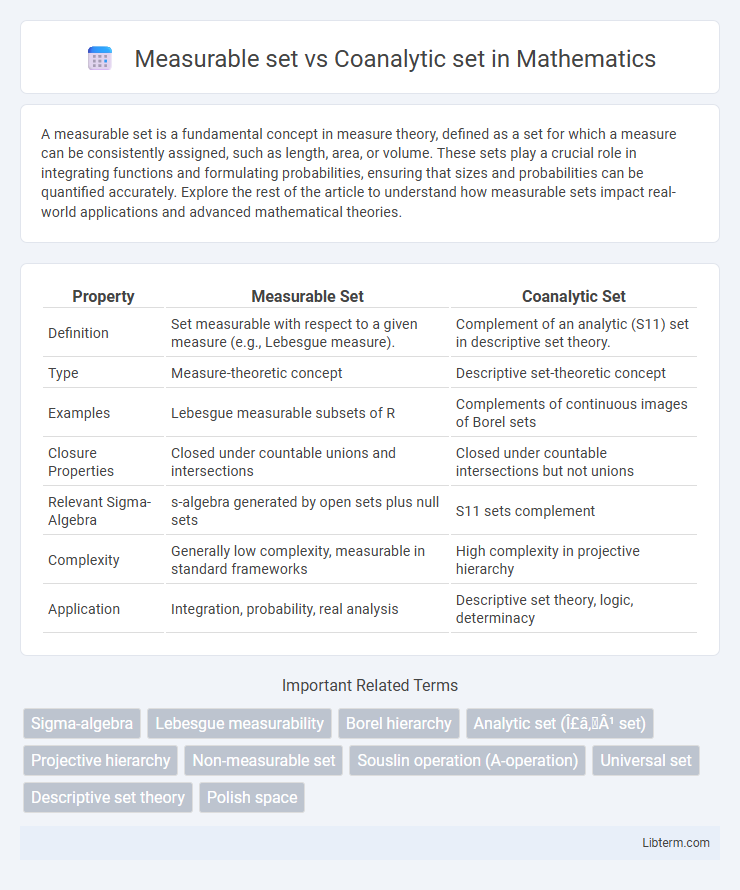
| Property | Measurable Set | Coanalytic Set |
|---|---|---|
| Definition | Set measurable with respect to a given measure (e.g., Lebesgue measure). | Complement of an analytic (S11) set in descriptive set theory. |
| Type | Measure-theoretic concept | Descriptive set-theoretic concept |
| Examples | Lebesgue measurable subsets of R | Complements of continuous images of Borel sets |
| Closure Properties | Closed under countable unions and intersections | Closed under countable intersections but not unions |
| Relevant Sigma-Algebra | s-algebra generated by open sets plus null sets | S11 sets complement |
| Complexity | Generally low complexity, measurable in standard frameworks | High complexity in projective hierarchy |
| Application | Integration, probability, real analysis | Descriptive set theory, logic, determinacy |
Introduction to Measurable and Coanalytic Sets
Measurable sets in measure theory are subsets of a given space for which a measure, such as the Lebesgue measure, is well-defined and adheres to countable additivity, forming the foundation of integration and probability theory. Coanalytic sets, also known as P11 sets in descriptive set theory, are complements of analytic sets and represent a higher level of complexity in the projective hierarchy, often studied for their intricate definability and structural properties. Understanding measurable and coanalytic sets involves exploring their roles in different mathematical frameworks where measurability addresses quantitative analysis, while coanalyticity captures descriptive complexity and definability beyond Borel sets.
Defining Measurable Sets in Measure Theory
Measurable sets in measure theory are defined by their compatibility with a given measure, typically characterized through the Caratheodory criterion, which ensures that the measure of any set can be approximated from measurable subsets. These sets form a s-algebra, allowing countable operations that preserve measurability and enabling integration theories like Lebesgue integration. Unlike coanalytic sets, which arise in descriptive set theory and are defined by their projective complexity, measurable sets are primarily concerned with their quantitative properties under measures.
Understanding Coanalytic Sets in Descriptive Set Theory
Coanalytic sets, also known as P11 sets, play a crucial role in descriptive set theory as complements of analytic (S11) sets within Polish spaces, exhibiting higher complexity than Borel sets but remaining definable through projective hierarchy levels. Unlike measurable sets, which are defined via measure theory and are key in integration and probability, coanalytic sets focus on definability and topological complexity without necessarily possessing measure properties. Understanding coanalytic sets involves analyzing their representation through projections of closed sets and their position in the projective hierarchy, providing insights into the classification of complex sets beyond the Borel framework.
Key Properties of Measurable Sets
Measurable sets in a s-algebra are characterized by their closure under countable unions, intersections, and complements, ensuring well-defined measures like Lebesgue measure. These sets satisfy countable additivity, allowing the measure of a union of disjoint measurable sets to equal the sum of their individual measures. Unlike coanalytic sets, which arise in descriptive set theory as complements of analytic sets and may lack full measurability, measurable sets provide a robust framework for integration and probability.
Essential Characteristics of Coanalytic Sets
Coanalytic sets, also known as P11 sets, are projective sets that are complements of analytic sets and exhibit closure under continuous preimages, distinguishing them from measurable sets in the context of descriptive set theory. Unlike measurable sets defined through s-algebras and measure theory, coanalytic sets are characterized by their definability via a universal quantifier over reals and are often non-Borel, reflecting complex structural properties. Essential characteristics of coanalytic sets include their stability under countable intersections, potential non-measurability in certain models of set theory, and significant roles in hierarchies beyond Borel and analytic classes.
Differences Between Measurable and Coanalytic Sets
Measurable sets, specifically Lebesgue measurable sets, are subsets of the real line with well-defined measure values allowing integration and probability assignments, whereas coanalytic sets belong to the projective hierarchy as complements of analytic sets and are often non-measurable or have complicated definability. Unlike measurable sets characterized primarily by measure-theoretic properties, coanalytic sets are analyzed through descriptive set theory focusing on their topological and definability complexity. Measurable sets form a sigma-algebra closed under countable unions and intersections, while coanalytic sets may lack closure properties typical of sigma-algebras and can exhibit complex structural features beyond measure theory.
Examples of Measurable vs. Coanalytic Sets
A measurable set in a standard measure space, such as a Borel set or any set in the completion of the Lebesgue measure, serves as a classical example of a measurable set with well-defined measure properties. In contrast, a coanalytic set, often arising in descriptive set theory, can be constructed as the complement of an analytic set, with examples including the set of all non-well-orderings of the natural numbers, which is coanalytic but not Borel measurable. These examples highlight that while measurable sets are well-behaved under measure and integrals, coanalytic sets may exhibit complex definability properties without guaranteed measurability in the Lebesgue sense.
Significance in Mathematical Analysis and Logic
Measurable sets, central to measure theory, enable rigorous integration and probability calculations by providing a framework for assigning consistent size or volume to subsets of a given space. Coanalytic sets, arising in descriptive set theory, hold significance in logic by representing complex definable sets beyond Borel hierarchy, often linked to projective determinacy and large cardinals. Their study deepens understanding of definability, hierarchies of complexity, and limits of measurability within mathematical analysis and foundational logic.
Common Applications and Implications
Measurable sets, fundamental in measure theory, enable precise quantification of size and probability, serving critical roles in probability theory and real analysis where integration and limit theorems apply. Coanalytic sets, prominent in descriptive set theory, often arise in logic and theoretical computer science, particularly in classification problems and definability within Polish spaces. Understanding the interplay between measurable and coanalytic sets facilitates advances in fields like ergodic theory, where measurable structures govern dynamical systems, and in computability theory, where coanalytic hierarchies classify problem complexities.
Open Problems and Research Directions
Measurable sets, defined within sigma-algebras and typically associated with Lebesgue measure, contrast sharply with coanalytic sets, which belong to the broader projective hierarchy and often lack classical measurability properties. Open problems in this area center on the interplay between descriptive set theory and measure theory, such as determining the precise conditions under which coanalytic sets can be rendered measurable or possess regularity properties like the Baire property. Current research directions pursue the development of advanced forcing techniques and large cardinal hypotheses to clarify the hierarchy of definability and measurability, aiming to resolve questions about the structure and classification of coanalytic sets within measurable frameworks.
Measurable set Infographic
 libterm.com
libterm.com