An automorphism is a concept in mathematics referring to a structure-preserving map from a mathematical object to itself, highlighting its symmetries. Understanding automorphisms helps reveal intrinsic properties and invariances within algebraic structures, graphs, or geometric figures. Explore this article to deepen your knowledge of automorphisms and their crucial role in various fields.
Table of Comparison
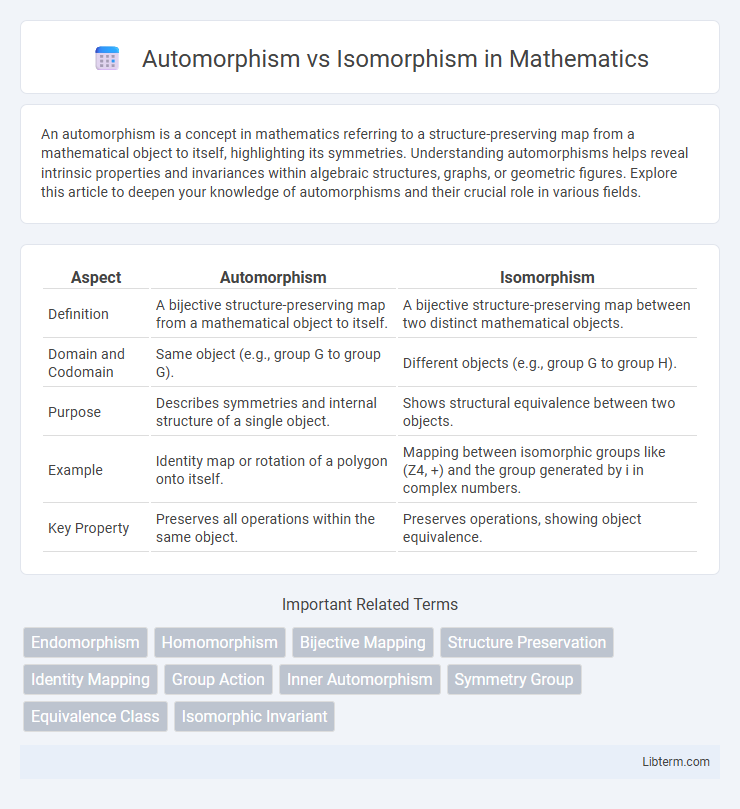
| Aspect | Automorphism | Isomorphism |
|---|---|---|
| Definition | A bijective structure-preserving map from a mathematical object to itself. | A bijective structure-preserving map between two distinct mathematical objects. |
| Domain and Codomain | Same object (e.g., group G to group G). | Different objects (e.g., group G to group H). |
| Purpose | Describes symmetries and internal structure of a single object. | Shows structural equivalence between two objects. |
| Example | Identity map or rotation of a polygon onto itself. | Mapping between isomorphic groups like (Z4, +) and the group generated by i in complex numbers. |
| Key Property | Preserves all operations within the same object. | Preserves operations, showing object equivalence. |
Introduction to Automorphism and Isomorphism
Automorphisms are structure-preserving maps from a mathematical object to itself, highlighting its internal symmetries, while isomorphisms are bijective mappings between two objects that indicate structural equivalence. In group theory or graph theory, automorphisms reveal invariant properties within a single object, whereas isomorphisms establish a correspondence that shows two objects are essentially indistinguishable in terms of their structure. Understanding automorphisms and isomorphisms is essential for analyzing symmetry, equivalence, and classification in algebraic and combinatorial contexts.
Definitions: Automorphism Explained
An automorphism is a bijective homomorphism from a mathematical object to itself, preserving its entire structure and properties. It serves as a symmetry transformation within algebraic structures like groups, rings, or graphs, maintaining both operations and relations unchanged. This concept is crucial for understanding internal symmetries and self-equivalences in algebra and geometry.
Understanding Isomorphism
Isomorphism in mathematics refers to a structure-preserving bijection between two objects, indicating they are fundamentally identical in structure despite possible differences in appearance. Understanding isomorphism involves recognizing how mappings maintain operations and relations, ensuring structural equivalence in areas such as group theory, graph theory, and algebra. This concept is central to classifying objects by their intrinsic properties rather than superficial differences, distinguishing it from automorphism, which is an isomorphism from an object to itself.
Key Differences Between Automorphism and Isomorphism
Automorphism is a structure-preserving map from a mathematical object to itself, highlighting symmetries within a single object, while isomorphism is a bijective map between two distinct objects that preserves structure, establishing their equivalence. Automorphisms form a group known as the automorphism group, whereas isomorphisms classify objects up to structural similarity without forming a group themselves. The main difference lies in the domain and codomain being identical for automorphisms, whereas isomorphisms connect different objects.
Mathematical Significance of Automorphisms
Automorphisms reveal the intrinsic symmetries of mathematical structures by mapping an object onto itself while preserving its operations, providing critical insight into its internal symmetry group. Unlike isomorphisms, which establish equivalence between distinct structures, automorphisms highlight invariant properties and enable classification through group actions on the structure. The study of automorphism groups is fundamental in fields like group theory, algebraic geometry, and topology, as they encode structural rigidities and symmetries essential for understanding complex mathematical objects.
The Role of Isomorphisms in Abstract Algebra
Isomorphisms in abstract algebra establish structural equivalence between algebraic objects such as groups, rings, or fields, preserving operations and properties through bijective homomorphisms. Automorphisms are isomorphisms from an algebraic structure onto itself, revealing internal symmetries that help classify objects and understand their invariant features. The study of isomorphisms enables mathematicians to identify when two seemingly different algebraic systems are fundamentally the same, facilitating deeper insights into their behavior and applications.
Examples Illustrating Automorphism vs Isomorphism
An automorphism of a mathematical object, such as a group or graph, is an isomorphism from the object onto itself, exemplified by the rotation symmetry of a square that maps the square onto itself preserving structure. In contrast, an isomorphism relates two distinct objects, such as the isomorphism between the group of integers modulo 4 and the group of fourth roots of unity, establishing structural equivalence without identity. Examples include the automorphisms of the cyclic group \( C_4 \), which consist of mappings like \( a \mapsto a^3 \), while an isomorphism example is the bijective function \( f : \mathbb{Z}_4 \to \{1, i, -1, -i\} \) in complex numbers under multiplication.
Applications in Graph Theory and Group Theory
Automorphisms in graph theory reveal symmetries by mapping a graph onto itself while preserving vertex connectivity, crucial for network analysis and graph classification tasks. Isomorphisms identify structural equivalences between different graphs or groups, enabling the comparison of algebraic structures in group theory and proving the equivalence of seemingly distinct networks. Both concepts facilitate the understanding of invariant properties and structural patterns, essential for solving graph isomorphism problems and classifying groups by their structural characteristics.
Common Misconceptions and Clarifications
Automorphisms are isomorphisms from a mathematical object to itself, preserving its structure, while isomorphisms relate two distinct objects with an identical structure. A common misconception is that automorphisms always imply trivial identity mappings, but they can include complex symmetries that reveal internal structure. Understanding that isomorphisms indicate equivalence between objects and automorphisms describe self-symmetry clarifies their distinct but related roles in algebra and graph theory.
Conclusion: Choosing Between Automorphism and Isomorphism
Choosing between automorphism and isomorphism depends on the context of structure analysis: automorphisms emphasize internal symmetries within a single algebraic structure, revealing its self-equivalences, while isomorphisms identify structural equivalences between two distinct objects. In fields such as group theory and graph theory, automorphisms help characterize an object's invariants, whereas isomorphisms facilitate classification and comparison across different objects. Understanding whether the focus is on intrinsic symmetry or inter-object equivalence guides the appropriate application of automorphism or isomorphism concepts.
Automorphism Infographic
 libterm.com
libterm.com