A pullback is a fundamental construction in category theory that allows you to combine two morphisms with a common codomain into a universal object, capturing their relationships precisely. The direct product, on the other hand, provides a way to form a new object from two objects in a category, representing them together while preserving their individual structures. Explore the rest of the article to understand how these concepts interconnect and apply in various mathematical contexts.
Table of Comparison
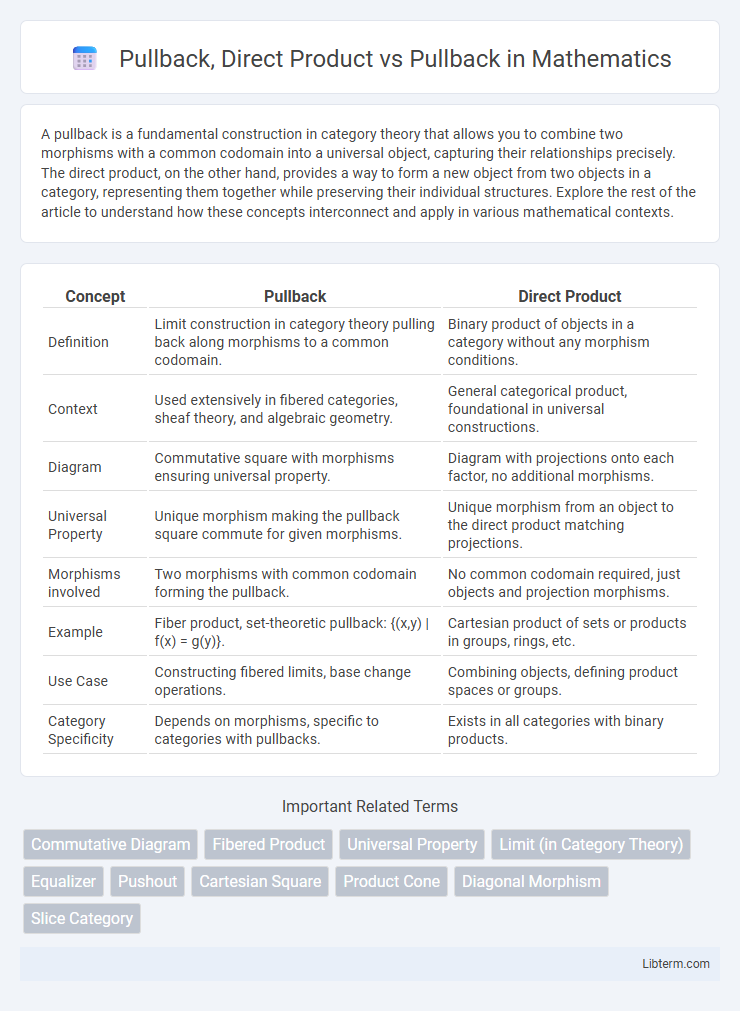
| Concept | Pullback | Direct Product |
|---|---|---|
| Definition | Limit construction in category theory pulling back along morphisms to a common codomain. | Binary product of objects in a category without any morphism conditions. |
| Context | Used extensively in fibered categories, sheaf theory, and algebraic geometry. | General categorical product, foundational in universal constructions. |
| Diagram | Commutative square with morphisms ensuring universal property. | Diagram with projections onto each factor, no additional morphisms. |
| Universal Property | Unique morphism making the pullback square commute for given morphisms. | Unique morphism from an object to the direct product matching projections. |
| Morphisms involved | Two morphisms with common codomain forming the pullback. | No common codomain required, just objects and projection morphisms. |
| Example | Fiber product, set-theoretic pullback: {(x,y) | f(x) = g(y)}. | Cartesian product of sets or products in groups, rings, etc. |
| Use Case | Constructing fibered limits, base change operations. | Combining objects, defining product spaces or groups. |
| Category Specificity | Depends on morphisms, specific to categories with pullbacks. | Exists in all categories with binary products. |
Introduction to Pullback and Direct Product
Pullback is a categorical construction that creates a new object representing the universal solution to a pair of morphisms with a common codomain, effectively capturing their fibered product. Direct product, in contrast, is a straightforward construction combining two objects into an ordered pair within the same category, preserving their individual structures independently. Understanding pullback involves grasping its role in fibered categories and limits, while the direct product emphasizes Cartesian product structures in category theory.
Understanding Pullback in Category Theory
Pullback in category theory represents a limit that defines the most general object fitting two morphisms with a common codomain, capturing their universal property precisely. Unlike the direct product, which combines objects independently, a pullback encodes dependencies between morphisms, ensuring compositional compatibility. This construction is fundamental for understanding fibered products, equalizers, and gluing constructions across various categories, highlighting its versatility and centrality in category-theoretic frameworks.
The Concept of Direct Product Explained
The concept of direct product in category theory involves constructing an object that represents the product of two given objects, along with projection morphisms satisfying a universal property. A pullback is a special case of a limit that captures the product of two morphisms with a common codomain, preserving the structure and relationships in the category. Understanding direct products aids in comprehending pullbacks as both involve universal properties linking objects and morphisms within a categorical framework.
Differences Between Pullback and Direct Product
Pullback and direct product are both categorical constructions but differ fundamentally in their universal properties and context of use. A direct product combines objects by taking their product without any imposed compatibility conditions, while a pullback defines a limit that enforces a commutative square with given morphisms, ensuring the objects meet specific alignment criteria. The pullback often appears as a fibered product in contexts requiring synchronization of morphisms, whereas the direct product serves as a more general, structure-preserving combination without morphism constraints.
Mathematical Definition of Pullback
Pullback in category theory is defined as the limit of a diagram consisting of two morphisms with a common codomain, capturing the universal construction that "pulls back" along these morphisms. Unlike direct product, which combines objects without reference to morphisms, the pullback enforces a commutative square ensuring compatibility between morphisms. Formally, given morphisms \(f: X \to Z\) and \(g: Y \to Z\), the pullback is an object \(P\) with projections \(p_1: P \to X\) and \(p_2: P \to Y\) satisfying \(f \circ p_1 = g \circ p_2\) and universal with respect to this property.
Properties of Direct Product
The direct product in category theory preserves product projections and allows factorization through universal morphisms, exhibiting a strong universal property that guarantees unique mediating morphisms. Unlike pullbacks, direct products do not necessarily reflect morphism limitations or fibered structures but prioritize componentwise construction, enabling parallel composition of objects. This property ensures that any morphism from an object into the product corresponds uniquely to a pair of morphisms into each component, facilitating straightforward manipulation of product objects in Cartesian categories.
Examples Illustrating Pullback
Pullbacks in category theory generalize the notion of fibered products, representing the universal construction that combines objects via morphisms into a common codomain. An example involves sets: given functions f: A - C and g: B - C, their pullback is the subset of A x B consisting of pairs (a, b) where f(a) = g(b). This construction contrasts with direct products, which simply pair elements without considering morphism compatibility, while pullbacks enforce a commutative square reflecting the limiting property in the categorical context.
Applications of Direct Product and Pullback
Direct products enable the combination of multiple algebraic structures into a single entity, facilitating the study of their simultaneous properties in group theory, ring theory, and module theory. Pullbacks serve as a tool for constructing fibered products in category theory, crucial for defining limits and for applications in algebraic geometry and topology. Both constructions are instrumental in solving extension problems and analyzing morphisms between structured sets.
Pullback vs Direct Product in Different Categories
Pullbacks and direct products serve distinct purposes in category theory: pullbacks represent the universal construction for fibered products, capturing limits of diagrams with two morphisms to a common codomain, while direct products provide a universal construction combining objects side-by-side without mapping constraints. In the category of sets, pullbacks correspond to set-theoretic fibered products, aligning with intersections, whereas direct products represent Cartesian products, pairing elements independently. In contrast, categories like groups or topological spaces maintain these structural differences, with pullbacks preserving morphism compatibilities and direct products forming objects with component-wise operations or structures.
Summary: Choosing Between Pullback and Direct Product
Pullbacks and direct products serve different categorical purposes: pullbacks combine objects over a shared morphism to model fibered structures, while direct products pair objects independently without imposed relationships. Selecting pullbacks is optimal when preserving commutative diagrams and contextual dependencies, crucial in sheaf theory and limit constructions. Direct products suit scenarios requiring simple Cartesian pairing without morphism constraints, common in product topology and universal constructions.
Pullback, Direct Product Infographic
 libterm.com
libterm.com