A tangential base point is a concept in algebraic geometry used to study the fundamental group of a space when a conventional base point is unavailable or inconvenient. It involves choosing a direction or tangent vector at a singularity or limit point to serve as a reference for loops and paths. Explore the rest of the article to understand how tangential base points enhance your grasp of fundamental group calculations.
Table of Comparison
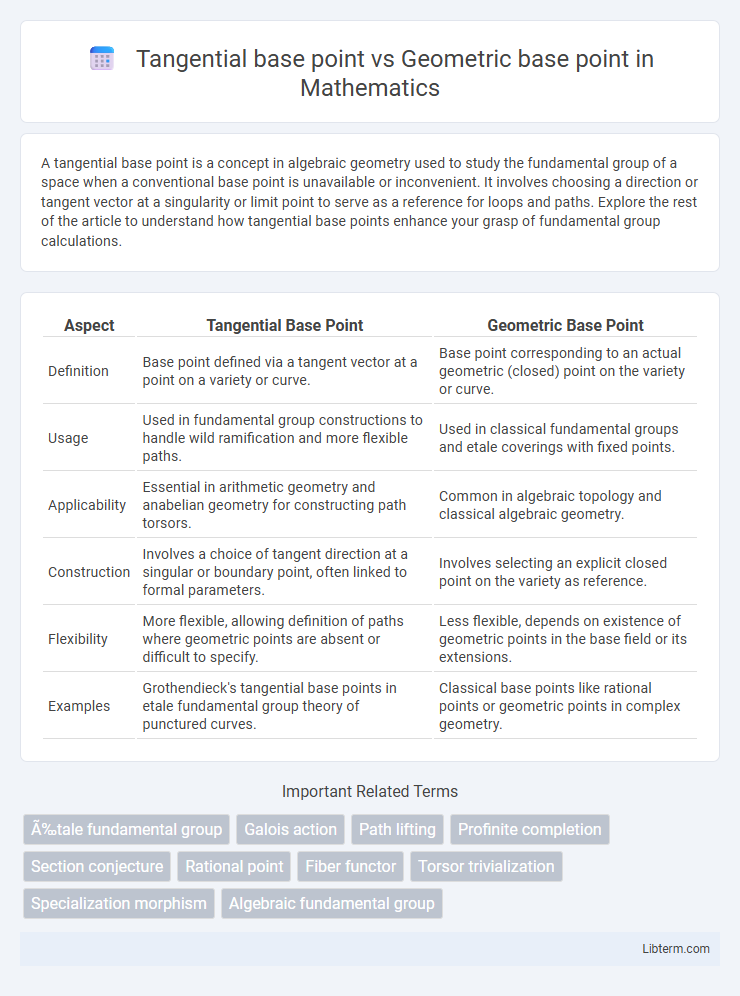
| Aspect | Tangential Base Point | Geometric Base Point |
|---|---|---|
| Definition | Base point defined via a tangent vector at a point on a variety or curve. | Base point corresponding to an actual geometric (closed) point on the variety or curve. |
| Usage | Used in fundamental group constructions to handle wild ramification and more flexible paths. | Used in classical fundamental groups and etale coverings with fixed points. |
| Applicability | Essential in arithmetic geometry and anabelian geometry for constructing path torsors. | Common in algebraic topology and classical algebraic geometry. |
| Construction | Involves a choice of tangent direction at a singular or boundary point, often linked to formal parameters. | Involves selecting an explicit closed point on the variety as reference. |
| Flexibility | More flexible, allowing definition of paths where geometric points are absent or difficult to specify. | Less flexible, depends on existence of geometric points in the base field or its extensions. |
| Examples | Grothendieck's tangential base points in etale fundamental group theory of punctured curves. | Classical base points like rational points or geometric points in complex geometry. |
Introduction to Mathematical Base Points
Mathematical base points serve as reference markers in algebraic geometry, where geometric base points denote fixed locations on a variety integral to defining morphisms or families of varieties. Tangential base points extend this concept by incorporating tangent directions at singularities, enabling refined path or loop considerations in fundamental group studies. Understanding the distinction and application of geometric versus tangential base points is crucial for advanced analyses in algebraic topology and arithmetic geometry.
Definition of Geometric Base Point
A geometric base point in algebraic geometry is a fixed reference point chosen on a variety, often defined over an algebraically closed field, used to study the fundamental group and coverings of the variety. It contrasts with a tangential base point, which is defined using a tangent vector at a boundary point or point at infinity, providing a way to probe the local geometry near singularities or missing points. The geometric base point serves as a concrete anchor for constructing path spaces and defining monodromy representations in etale fundamental group theory.
Understanding Tangential Base Point
A tangential base point in algebraic geometry is a formal device used to define base points on curves or schemes where no conventional geometric point exists, often represented by a tangent vector at a point on the boundary. Unlike geometric base points, which correspond to actual points on a variety or scheme, tangential base points enable the study of fundamental groups and monodromy actions in degenerating families by providing a consistent limit object. This concept is crucial for understanding the etale fundamental group in situations where traditional base points cannot be chosen, allowing for refined constructions in arithmetic geometry and topology.
Historical Context and Motivation
Tangential base points emerged in algebraic geometry during the 1960s as a refinement of geometric base points to overcome limitations in studying fundamental groups of algebraic varieties. Grothendieck introduced tangential base points to enable defining paths and monodromy representations when no rational points exist, particularly in the context of etale fundamental groups. This innovation addressed challenges in connecting algebraic and topological fundamental groups, enhancing the understanding of covering spaces and Galois actions.
Key Differences Between Tangential and Geometric Base Points
Tangential base points in algebraic geometry refer to base points defined by tangent directions or infinitesimal neighborhoods, whereas geometric base points correspond to actual points on an algebraic variety or scheme. The key difference lies in their nature: geometric base points are concrete points used for defining fiber functors, while tangential base points capture more refined local information, often used in fundamental group studies to distinguish paths up to infinitesimal homotopies. This distinction is crucial in Grothendieck's theory of etale fundamental groups, where tangential base points enable analyzing coverings in settings lacking rational points.
Applications in Algebraic Geometry
Tangential base points serve as essential tools for studying the fundamental group of algebraic varieties by allowing paths to start from infinitesimal directions, thus refining monodromy representations in etale and profinite settings. Geometric base points, often chosen as rational or geometric points over an algebraic closure, provide fixed reference points in the etale fundamental group, facilitating concrete computations and comparisons between fiber functors. Applications in algebraic geometry leverage tangential base points in Grothendieck-Teichmuller theory and deformation problems, while geometric base points underpin classical Galois actions and the study of motivic fundamental groups.
Role in Fundamental Group Calculations
Tangential base points facilitate fundamental group calculations by providing a well-defined reference in situations where geometric base points are not easily accessible, such as algebraic curves with singularities or over non-algebraically closed fields. Geometric base points correspond to actual points on a space, enabling straightforward loop constructions for fundamental groups, while tangential base points use tangent directions to define equivalence classes of paths, extending the scope of monodromy representations. This distinction is crucial in algebraic geometry and number theory, as tangential base points allow for refined fundamental group computations that encode additional arithmetic and geometric information.
Tangential Base Points in Galois Theory
Tangential base points in Galois theory provide a refined framework to study the fundamental group of algebraic varieties, especially when geometric base points are inaccessible or inconvenient. These points are defined via formal neighborhoods along tangent directions, allowing the formulation of path spaces and Galois actions in situations where traditional geometric base points do not exist. The use of tangential base points enhances the understanding of etale fundamental groups and their automorphisms, playing a crucial role in Grothendieck's theory of anabelian geometry.
Advantages and Limitations of Each Approach
Tangential base points offer advantages in algebraic geometry by enabling the study of monodromy and fundamental group actions near singularities, providing finer control over local branching behaviors than geometric base points. However, their abstract nature and dependence on tangent directions make them more challenging to visualize and apply in topological settings, potentially complicating intuition and computations. Geometric base points, being concrete points on the space, facilitate more direct interpretations and simpler homotopy analyses but may lack the sensitivity to capture subtle local structures around singularities that tangential base points reveal.
Conclusion: Choosing the Right Base Point
Choosing the right base point depends on the specific context of algebraic geometry or topology; tangential base points offer flexibility in dealing with fundamental groups of schemes when traditional geometric points are unavailable or insufficient. Geometric base points provide a more intuitive and canonical reference rooted in actual points of a geometric object, essential for classical approaches and visualization. Ultimately, the selection hinges on the problem's nature, with tangential base points favored in advanced arithmetic geometry and geometric base points preferred in classical topological or geometric settings.
Tangential base point Infographic
 libterm.com
libterm.com