Intersection product is a fundamental operation in algebraic geometry and topology that quantifies the way subspaces intersect within a given space, capturing important geometric and topological information. It enables you to compute intersection numbers, which are essential in the study of varieties, cycles, and cohomology classes. Explore the rest of the article to understand how intersection products apply in various mathematical contexts and their computational techniques.
Table of Comparison
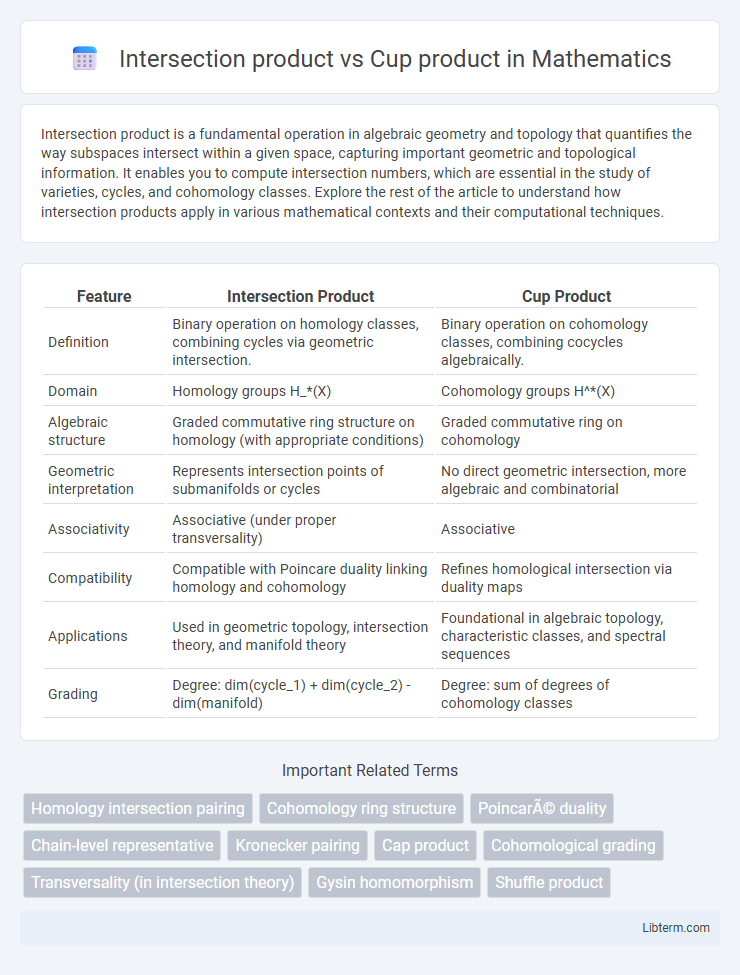
| Feature | Intersection Product | Cup Product |
|---|---|---|
| Definition | Binary operation on homology classes, combining cycles via geometric intersection. | Binary operation on cohomology classes, combining cocycles algebraically. |
| Domain | Homology groups H_*(X) | Cohomology groups H^*(X) |
| Algebraic structure | Graded commutative ring structure on homology (with appropriate conditions) | Graded commutative ring on cohomology |
| Geometric interpretation | Represents intersection points of submanifolds or cycles | No direct geometric intersection, more algebraic and combinatorial |
| Associativity | Associative (under proper transversality) | Associative |
| Compatibility | Compatible with Poincare duality linking homology and cohomology | Refines homological intersection via duality maps |
| Applications | Used in geometric topology, intersection theory, and manifold theory | Foundational in algebraic topology, characteristic classes, and spectral sequences |
| Grading | Degree: dim(cycle_1) + dim(cycle_2) - dim(manifold) | Degree: sum of degrees of cohomology classes |
Introduction to Intersection Product and Cup Product
Intersection product in algebraic topology refers to the operation that assigns an intersection number to pairs of homology classes in a manifold, capturing their geometric intersection behavior. The cup product is a cohomological operation that combines two cohomology classes to produce a new one in a higher degree, encoding algebraic structure in cohomology rings. Both products reveal dual aspects of manifold topology, linking geometric intersections with algebraic invariants through Poincare duality.
Algebraic Topology: The Role of Products
The intersection product in algebraic topology captures the geometric interaction of submanifolds within a manifold, representing their transversal intersection classes in homology. The cup product, defined in cohomology, encodes the algebraic structure of cochains by combining classes through the cochain-level operation that reflects intersection patterns in dual homology. Both products play crucial roles in understanding manifold topology, with the intersection product relating to Poincare duality and the cup product providing a graded ring structure fundamental for calculations in cohomology theory.
Defining the Intersection Product
The intersection product in algebraic topology is defined by pairing homology classes of complementary dimensions to produce a homology class, using transverse intersections of cycles in a manifold. It relies on Poincare duality, identifying homology classes with cohomology classes and translating geometric intersections into algebraic terms. This product captures the intersection behavior of submanifolds and serves as a geometric counterpart to the cup product in cohomology.
Understanding the Cup Product in Cohomology
The cup product in cohomology is an algebraic operation that combines cohomology classes to form a graded ring structure, reflecting the intersection behavior of cycles in homology. It is defined using the cochain-level product and respects the grading, making it a fundamental tool for distinguishing topological spaces through their cohomology rings. Understanding the cup product involves analyzing how cocycles interact under the cup operation, revealing information about the space's global geometric structure and linking with intersection products via Poincare duality in oriented manifolds.
Geometric Interpretation of Intersection Product
The Intersection product in algebraic topology represents the geometric overlap of submanifolds within a given manifold, measuring how cycles intersect transversely to form new homology classes. It provides a tangible geometric interpretation by counting intersection points with orientation signs, reflecting how subspaces meet inside the ambient space. This contrasts with the Cup product, which is primarily an algebraic operation on cohomology classes without a direct geometric visualization of intersecting cycles.
Algebraic Formulation of the Cup Product
The cup product in cohomology is algebraically formulated using cochain maps that combine cochains to produce higher-degree cochains, providing a graded-commutative ring structure on the cohomology groups. It arises from the composition of the Alexander-Whitney or Eilenberg-Zilber chain approximations to the diagonal map in singular (co)homology, encoding how cochains interact on chains of product spaces. Unlike the geometric intersection product in homology, which counts transverse intersections of submanifolds, the cup product is fundamentally an algebraic operation defined on the cochain complex level, capturing topological information via algebraic structures.
Key Differences Between Intersection and Cup Products
The intersection product operates within homology, combining the classes of intersecting submanifolds to produce a new homology class reflecting their geometric intersection, whereas the cup product acts in cohomology, merging cohomology classes to yield higher-degree classes via algebraic operations on differential forms or cocycles. Intersection products rely on transversal intersection and orientability conditions to define a geometric intersection number, while cup products depend on the algebraic structure of cochain complexes and their induced graded ring. The key difference lies in their domain--homology for intersection products versus cohomology for cup products--and their interpretation as geometric versus algebraic constructs respectively.
Applications in Topology and Geometry
The intersection product and cup product serve crucial roles in algebraic topology and geometry for quantifying how subspaces and cohomology classes interact within manifolds. The intersection product operates on homology classes, measuring geometric intersections of submanifolds to reveal topological invariants like intersection numbers, fundamental in studying oriented manifolds and Poincare duality. The cup product acts on cohomology classes, encoding the algebraic structure of cohomology rings and facilitating calculations of characteristic classes, aiding classifications of fiber bundles and detecting manifold properties such as orientability and complex structure.
Relationship Between Intersection Product and Cup Product
The intersection product in homology and the cup product in cohomology are related through Poincare duality, linking homology classes and cohomology classes in an oriented manifold. Specifically, the intersection product of two homology classes corresponds to the cup product of their Poincare dual cohomology classes. This correspondence provides a powerful algebraic framework to translate geometric intersection data into cohomological operations and vice versa.
Conclusion: Choosing the Right Product for Mathematical Problems
The intersection product is best suited for geometric contexts involving oriented manifolds and homology, where it captures the actual intersection behavior of subspaces. The cup product operates in cohomology and is essential for algebraic computations, encoding cohomological structure via a graded ring. Selecting between the intersection and cup product depends on whether the problem emphasizes geometric intersections and homology classes or algebraic manipulation within cohomology rings.
Intersection product Infographic
 libterm.com
libterm.com