An affine bundle is a fiber bundle whose fibers are affine spaces modeled on a vector space, enabling smooth transitions reflecting affine transformations. This structure plays a significant role in differential geometry and theoretical physics, particularly in the study of connections and gauge theories. Discover how affine bundles can enhance your understanding of geometric frameworks in the full article.
Table of Comparison
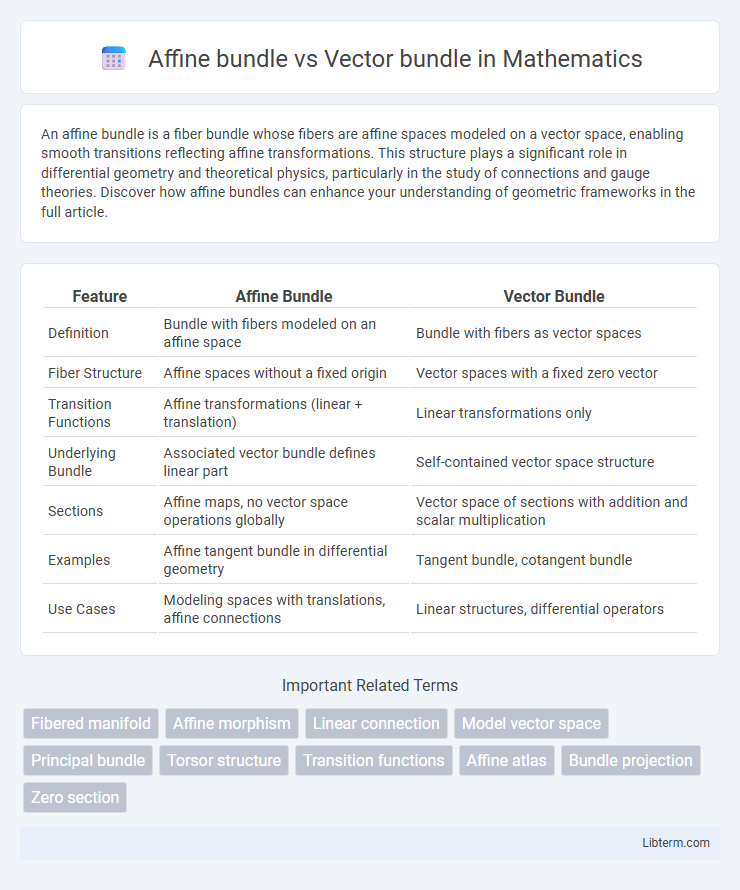
| Feature | Affine Bundle | Vector Bundle |
|---|---|---|
| Definition | Bundle with fibers modeled on an affine space | Bundle with fibers as vector spaces |
| Fiber Structure | Affine spaces without a fixed origin | Vector spaces with a fixed zero vector |
| Transition Functions | Affine transformations (linear + translation) | Linear transformations only |
| Underlying Bundle | Associated vector bundle defines linear part | Self-contained vector space structure |
| Sections | Affine maps, no vector space operations globally | Vector space of sections with addition and scalar multiplication |
| Examples | Affine tangent bundle in differential geometry | Tangent bundle, cotangent bundle |
| Use Cases | Modeling spaces with translations, affine connections | Linear structures, differential operators |
Introduction to Affine and Vector Bundles
Affine bundles are fiber bundles modeled on affine spaces, where fibers lack a distinguished origin but preserve affine structure, making them suitable for geometrical contexts involving translations without fixed points. Vector bundles have fibers that are vector spaces with a well-defined zero element, enabling linear operations like addition and scalar multiplication, fundamental in differential geometry and topology. The transition functions of affine bundles differ from vector bundles by incorporating affine transformations rather than linear ones, reflecting their inherent geometric differences.
Defining Vector Bundles: Structure and Properties
A vector bundle is a topological space consisting of a base space and a vector space attached to each point, equipped with a linear structure that allows for vector addition and scalar multiplication within each fiber. The local triviality condition ensures that around every point in the base space, the bundle resembles a Cartesian product of an open neighborhood and a fixed vector space. Transition functions of vector bundles are required to be linear isomorphisms, preserving the vector space structure across overlapping neighborhoods.
Understanding Affine Bundles: Core Concepts
Affine bundles generalize vector bundles by incorporating an affine space structure instead of a purely linear one, allowing fibers to be affine spaces modeled on a vector bundle. Unlike vector bundles, affine bundles lack a canonical zero section, making their transition functions affine transformations rather than linear maps. Understanding affine bundles involves grasping how the underlying vector bundle provides the model space for the affine fibers, emphasizing the interplay between affine geometry and bundle theory.
Key Differences Between Affine Bundles and Vector Bundles
Affine bundles differ from vector bundles primarily by lacking a canonical zero section, meaning affine bundles are modeled on vector bundles without a fixed origin in each fiber. While vector bundles have fibers that are vector spaces allowing linear operations such as addition and scalar multiplication, affine bundles have fibers that are affine spaces, supporting only affine combinations of points. The transition functions of vector bundles are linear, whereas affine bundles utilize affine transformations, incorporating translations alongside linear maps.
Examples of Vector Bundles in Geometry
Vector bundles in geometry often appear as tangent bundles, where each fiber is the tangent space of a manifold, or as cotangent bundles, which consist of all cotangent vectors at each point. Other key examples include the Mobius strip, representing a non-trivial line bundle, and the trivial bundle over a manifold formed by the Cartesian product of the manifold and a vector space. These examples highlight how vector bundles enable local linear structures while capturing global topological properties.
Illustrative Cases of Affine Bundles
Affine bundles generalize vector bundles by allowing fibers to be affine spaces modeled on vector spaces, enabling the representation of geometric structures with translations but no fixed origin. Illustrative cases of affine bundles include the tangent bundle viewed as an affine bundle over a manifold when connections specify affine structures instead of canonical linear ones. These bundles are essential in gauge theory and mechanics, where fields or configurations require affine transformations rather than purely linear ones.
Transition Functions and Local Trivializations
Affine bundles generalize vector bundles by replacing vector space fibers with affine spaces modeled on vector spaces, where transition functions are affine transformations combining linear maps with translations. Local trivializations of affine bundles consist of charts mapping fibers to affine spaces that vary smoothly over the base, differing from vector bundle trivializations which are purely linear and coordinate changes involve only linear isomorphisms. The transition functions for vector bundles form a linear representation in the general linear group, whereas affine bundle transitions belong to the affine group, encompassing both linear parts and affine shifts.
Applications of Affine and Vector Bundles
Affine bundles model geometric structures where transition functions are affine transformations, crucial in differential geometry for describing connections and gauge theories, especially in fiber bundle frameworks involving torsors over vector bundles. Vector bundles provide the foundation for linear algebraic structures on manifolds, extensively used in fields like quantum field theory, complex geometry, and index theory, supporting sections that form vector spaces fiberwise. In applications, affine bundles enable the treatment of parallel transport and affine connections without choosing a zero section, while vector bundles facilitate analysis of linear operators, characteristic classes, and cohomological invariants.
Relationship Between Affine Space and Vector Space
An affine bundle generalizes a vector bundle by replacing vector spaces with affine spaces, which lack a canonical origin but maintain a transitive and free action of an associated vector space. Each fiber of an affine bundle is modeled on an affine space whose difference vectors form a vector space corresponding to the fibers of a vector bundle. This relationship highlights that affine bundles can be viewed as torsors over vector bundles, emphasizing the underlying vector space structure governing the affine geometry.
Summary: Choosing Between Affine and Vector Bundles
Affine bundles generalize vector bundles by allowing fibers to be affine spaces modeled on vector spaces, suited for contexts lacking a canonical zero element. Vector bundles possess linear structure with distinguished zero sections, making them ideal for linear algebraic operations and modules over function rings. Choosing between them depends on whether linearity and zero elements are essential (vector bundles) or if translation-invariant structures without fixed origins (affine bundles) better capture the geometric framework.
Affine bundle Infographic
 libterm.com
libterm.com