Effective filtration improves air and water quality by removing contaminants and particles that can harm health and the environment. Advanced filtration technologies, such as HEPA filters and activated carbon, provide enhanced protection against allergens, pollutants, and toxins. Explore the rest of the article to learn how filtration systems can benefit your home or business.
Table of Comparison
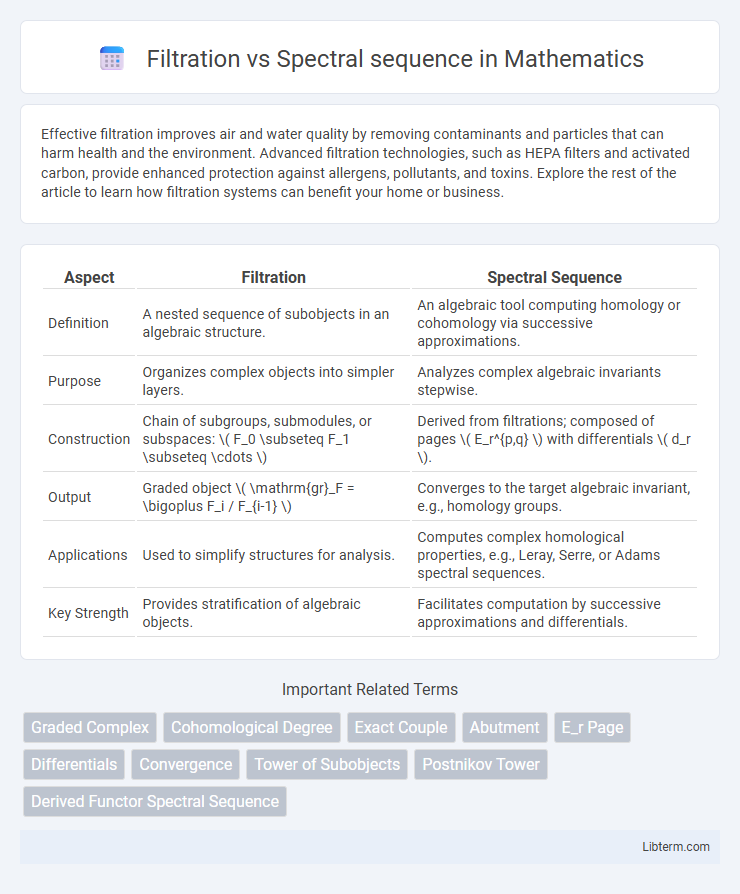
| Aspect | Filtration | Spectral Sequence |
|---|---|---|
| Definition | A nested sequence of subobjects in an algebraic structure. | An algebraic tool computing homology or cohomology via successive approximations. |
| Purpose | Organizes complex objects into simpler layers. | Analyzes complex algebraic invariants stepwise. |
| Construction | Chain of subgroups, submodules, or subspaces: \( F_0 \subseteq F_1 \subseteq \cdots \) | Derived from filtrations; composed of pages \( E_r^{p,q} \) with differentials \( d_r \). |
| Output | Graded object \( \mathrm{gr}_F = \bigoplus F_i / F_{i-1} \) | Converges to the target algebraic invariant, e.g., homology groups. |
| Applications | Used to simplify structures for analysis. | Computes complex homological properties, e.g., Leray, Serre, or Adams spectral sequences. |
| Key Strength | Provides stratification of algebraic objects. | Facilitates computation by successive approximations and differentials. |
Introduction to Filtration and Spectral Sequence
Filtration in algebraic topology and homological algebra refers to an increasing sequence of subobjects that decompose complex structures into simpler layers, facilitating detailed analysis. Spectral sequences arise as computational tools that systematically process these filtrations, providing successive approximations to the homology or cohomology of filtered complexes. The interplay between filtrations and spectral sequences enables the breakdown of complicated algebraic invariants into tractable stages, advancing the study of topological spaces and chain complexes.
Defining Filtration in Algebraic Topology
Filtration in algebraic topology is a nested sequence of subcomplexes \( \{F_pX\}_{p \in \mathbb{Z}} \) satisfying \( F_pX \subseteq F_{p+1}X \) that provides a hierarchical structure on a topological space or chain complex. This filtration induces a graded structure that is fundamental for constructing spectral sequences, enabling stepwise approximation of homology groups. By analyzing the associated graded objects \( \text{Gr}_p X = F_pX / F_{p-1}X \), one can extract algebraic invariants that track topological features across filtration levels.
What is a Spectral Sequence?
A spectral sequence is a computational tool in algebraic topology and homological algebra that provides a systematic method for approximating the homology or cohomology groups of complex spaces through successive approximations. It arises from a filtered complex, where the filtration organizes the complex into layers, and the spectral sequence encodes the differential behavior between these layers via pages or terms \( E_r^{p,q} \) converging to the desired homological invariants. Spectral sequences generalize filtration by translating the layered structure into a multi-stage iterative process that refines algebraic invariants step-by-step, allowing complex computations to be broken down into more manageable stages.
Key Differences Between Filtration and Spectral Sequence
Filtration organizes a complex into a nested sequence of subcomplexes indexed by integers, providing a hierarchical structure that simplifies the analysis of homology. Spectral sequences arise from filtrations and serve as computational tools that progressively approximate the homology or cohomology of the original complex through successive pages and differentials. The key difference lies in filtration being a structural decomposition, while spectral sequences are dynamic computational processes derived from that structure to extract algebraic invariants.
Role of Filtration in Constructing Spectral Sequences
Filtration plays a crucial role in constructing spectral sequences by providing a hierarchical decomposition of complex algebraic or topological structures into simpler layers. Each step in the filtration generates graded pieces that serve as inputs for successive pages of the spectral sequence, allowing for systematic computation of homology or cohomology groups. This layered approach enables the extraction of detailed structural information that would be difficult to analyze directly.
Common Types of Filtrations
Common types of filtrations in algebraic topology and homological algebra include the increasing (or ascending) filtration, where subcomplexes form a nested sequence growing larger, and the decreasing (or descending) filtration, characterized by nested subcomplexes shrinking within the original complex. The skeletal filtration associated with CW-complexes and the filtration arising from a Leray spectral sequence are vital examples used to analyze topological and algebraic structures. These filtrations provide the foundational layers that spectral sequences use to compute homology or cohomology groups by iteratively approximating complex algebraic invariants.
Applications of Spectral Sequences
Spectral sequences serve as powerful computational tools in algebraic topology, algebraic geometry, and homological algebra by providing a systematic method to approximate complex homology and cohomology groups via successive approximations derived from filtrations. They enable the calculation of derived functors, analysis of fiber bundles, and study of exact couples, making them essential in understanding the structure of filtered complexes and graded objects. Applications include computing the Adams spectral sequence to analyze stable homotopy groups and using the Leray spectral sequence for sheaf cohomology in algebraic geometry.
Filtration Examples in Homology and Cohomology
Filtrations in homology and cohomology serve as hierarchical decompositions that facilitate the analysis of complex algebraic structures by revealing successive approximations of spaces or chain complexes. Classic examples include the filtration of singular chain complexes by skeletons of simplicial complexes, enabling the computation of homology via associated graded objects. In cohomology, filtrations arise naturally in the Cech cohomology of open covers, providing spectral sequences that converge to the desired cohomological invariants.
Advantages and Limitations of Each Approach
Filtration techniques provide a straightforward way to analyze complex algebraic structures by breaking them into simpler substructures, making computations more manageable for certain spectral sequences. Spectral sequences excel in encoding multi-layered algebraic information, allowing for systematic step-by-step approximations of homology or cohomology groups, but they often require intricate understanding and can be computationally intensive. Filtrations are typically more intuitive and easier to visualize, while spectral sequences offer deeper insights into the graded structures but may suffer from convergence issues and complicated differentials.
Filtration vs Spectral Sequence: Which to Use When?
Filtration provides a stepwise decomposition of a complex, allowing gradual simplification and convergence analysis, making it ideal for understanding underlying structures. Spectral sequences offer a powerful computational tool by systematically approximating homology or cohomology groups through successive pages, best suited for complex, multi-layered problems. Choosing between them depends on the problem's complexity and the need for explicit computations versus structural insights.
Filtration Infographic
 libterm.com
libterm.com