A closed set in topology is a set that contains all its limit points, meaning it includes every point where sequences within the set converge. Such sets are essential in understanding continuity, compactness, and boundary behavior in mathematical analysis. Explore the rest of this article to deepen your grasp of how closed sets influence various topological properties and their applications.
Table of Comparison
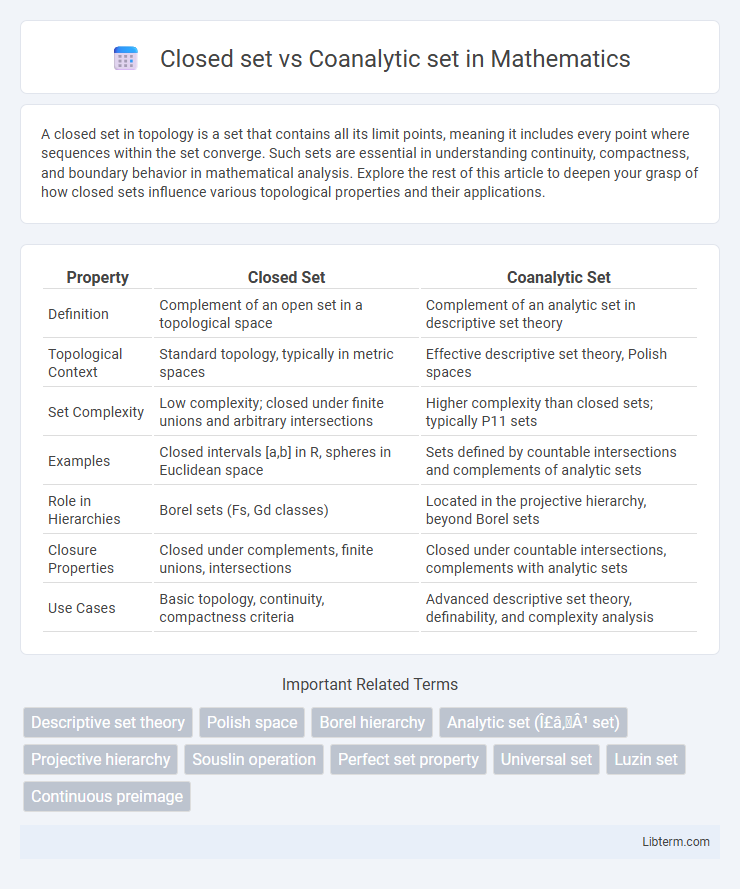
| Property | Closed Set | Coanalytic Set |
|---|---|---|
| Definition | Complement of an open set in a topological space | Complement of an analytic set in descriptive set theory |
| Topological Context | Standard topology, typically in metric spaces | Effective descriptive set theory, Polish spaces |
| Set Complexity | Low complexity; closed under finite unions and arbitrary intersections | Higher complexity than closed sets; typically P11 sets |
| Examples | Closed intervals [a,b] in R, spheres in Euclidean space | Sets defined by countable intersections and complements of analytic sets |
| Role in Hierarchies | Borel sets (Fs, Gd classes) | Located in the projective hierarchy, beyond Borel sets |
| Closure Properties | Closed under complements, finite unions, intersections | Closed under countable intersections, complements with analytic sets |
| Use Cases | Basic topology, continuity, compactness criteria | Advanced descriptive set theory, definability, and complexity analysis |
Understanding Closed Sets: Definition and Examples
Closed sets in topology are defined as sets that contain all their limit points, meaning any convergent sequence within the set has its limit also in the set. Examples of closed sets include the entire real line, finite sets, and intervals like [a, b], where the endpoints a and b are included. These sets contrast with coanalytic sets in descriptive set theory, which are complements of analytic sets and often appear in more complex hierarchical classifications.
Exploring Coanalytic Sets: Key Characteristics
Coanalytic sets, also known as P11 sets, are complements of analytic sets and arise in descriptive set theory as projections of closed sets in higher-dimensional spaces. Unlike closed sets, which are definable by straightforward topological closure properties, coanalytic sets exhibit more complex definability and often lack simple characterizations in standard Borel hierarchies. These sets are crucial in understanding projective hierarchies due to their intricate structure and their role in higher-level classification problems beyond closed and open sets.
Topological Foundations: How Sets Are Classified
Closed sets in topology are defined as those containing all their limit points, making them complements of open sets in a given topological space. Coanalytic sets, arising in descriptive set theory, belong to the projective hierarchy and are complements of analytic sets, showcasing a higher level of complexity compared to Borel sets and typically beyond closed sets in classification. The topological foundation of these classifications lies in their definability and the operations used to build them, where closed sets are characterized by simple closure properties, while coanalytic sets involve projections and complements of more complex definable sets within Polish spaces.
Closed vs. Coanalytic Sets: Main Differences
Closed sets are well-defined topological entities characterized by containing all their limit points within a given space, making them fundamental in classical analysis and topology. Coanalytic sets, also known as \(\Pi^1_1\) sets, belong to the projective hierarchy and are more complex, defined through projections of complements of analytic sets and often exhibiting higher descriptive set-theoretic complexity than closed sets. The main differences lie in their definability and complexity: closed sets are simpler and definable via standard topology, whereas coanalytic sets require advanced logical frameworks, highlighting distinctions in their structural and computational properties.
Descriptive Set Theory: Role of Closed and Coanalytic Sets
Closed sets in Descriptive Set Theory form the foundation of the Borel hierarchy, representing well-defined, topologically simple sets directly linked to open sets through complementation. Coanalytic sets, or P11 sets, extend beyond the Borel sets into the projective hierarchy, capturing more complex structures defined as complements of analytic sets, which are continuous images of Borel sets. The interplay between closed and coanalytic sets is crucial for understanding definability, measurability, and classification problems within the realm of Polish spaces.
Hierarchies in Set Theory: Where Closed and Coanalytic Sets Fit
Closed sets reside at the foundational level of the Borel hierarchy, specifically as P10 sets, representing the simplest definable topological sets. Coanalytic sets, positioned at the level P11 in the projective hierarchy, extend beyond Borel sets and capture more complex definability through analytic complements. The interplay between these hierarchies situates closed sets as baseline measurable entities, while coanalytic sets illustrate the increased complexity encountered in descriptive set theory's higher-level classifications.
Applications of Closed Sets in Mathematics
Closed sets play a fundamental role in topology, analysis, and related fields by providing essential frameworks for continuity, convergence, and compactness. They are utilized in defining important structures such as complete metric spaces and in proving fixed-point theorems, which have applications in differential equations and optimization. Unlike coanalytic sets, which arise in descriptive set theory with complex definability properties, closed sets serve as a foundational tool that supports practical problem-solving and theoretical developments throughout mathematics.
Uses and Significance of Coanalytic Sets
Coanalytic sets play a crucial role in descriptive set theory due to their complex definability and application in analyzing hierarchies beyond Borel sets. These sets are instrumental in studying projective sets, providing insights into determinacy, definability, and classification problems in mathematical logic. Unlike closed sets, which are simpler and easier to characterize, coanalytic sets help in understanding intricate structural properties of higher-level definable sets and their implications in effective descriptive set theory and recursion theory.
Examples Illustrating Closed and Coanalytic Sets
Closed sets include examples like closed intervals [0,1] in the real numbers, finite unions of such intervals, or the Cantor set, all of which are complements of open sets in a topological space. Coanalytic sets, often emerging in descriptive set theory, include complex examples such as the set of well-founded trees or the complement of an analytic set like the projection of a Borel set from a product space. These examples highlight the distinction: closed sets are topologically simple and well-understood, whereas coanalytic sets extend beyond Borel sets, capturing more intricate definability and hierarchy within Polish spaces.
Summary: Choosing Between Closed and Coanalytic Sets
Closed sets are well-defined by their boundary properties within a topological space, making them easier to handle in classical analysis and descriptive set theory. Coanalytic sets, as complements of analytic sets, possess more complex definability and often arise in higher-level classification problems, requiring advanced tools from effective descriptive set theory. Selecting between closed and coanalytic sets depends on the desired complexity and application context, with closed sets suitable for simpler, more concrete problems and coanalytic sets used for addressing intricate hierarchical or definability questions.
Closed set Infographic
 libterm.com
libterm.com