The module spectrum covers a wide range of functionalities crucial for modern software development, including communication protocols, data processing, and system integration. Understanding the full module spectrum enables you to select the right components for optimized performance and scalability. Discover how these modules work together by reading the full article.
Table of Comparison
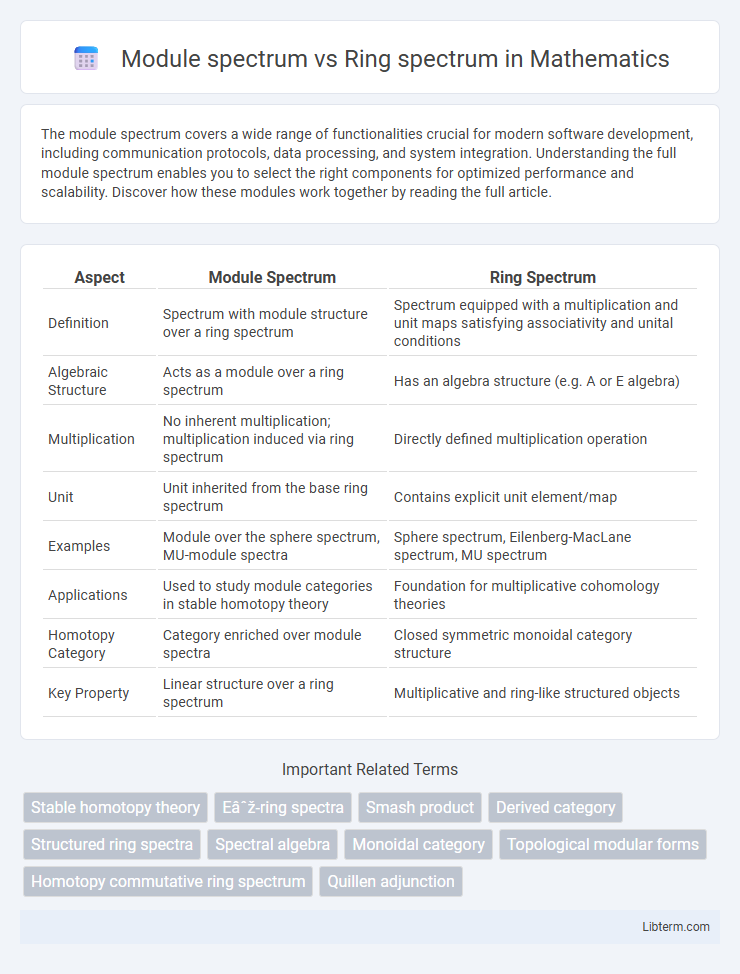
| Aspect | Module Spectrum | Ring Spectrum |
|---|---|---|
| Definition | Spectrum with module structure over a ring spectrum | Spectrum equipped with a multiplication and unit maps satisfying associativity and unital conditions |
| Algebraic Structure | Acts as a module over a ring spectrum | Has an algebra structure (e.g. A or E algebra) |
| Multiplication | No inherent multiplication; multiplication induced via ring spectrum | Directly defined multiplication operation |
| Unit | Unit inherited from the base ring spectrum | Contains explicit unit element/map |
| Examples | Module over the sphere spectrum, MU-module spectra | Sphere spectrum, Eilenberg-MacLane spectrum, MU spectrum |
| Applications | Used to study module categories in stable homotopy theory | Foundation for multiplicative cohomology theories |
| Homotopy Category | Category enriched over module spectra | Closed symmetric monoidal category structure |
| Key Property | Linear structure over a ring spectrum | Multiplicative and ring-like structured objects |
Defining Module Spectrum and Ring Spectrum
A module spectrum is a structured spectrum equipped with an action by a ring spectrum, serving as a generalized module over the ring spectrum in stable homotopy theory. A ring spectrum is a spectrum endowed with multiplication and unit maps that satisfy associativity and unital properties up to homotopy, effectively generalizing classical ring structures to the category of spectra. The distinction lies in the ring spectrum providing the algebraic structure, while the module spectrum represents objects that carry an action of this algebraic structure within the stable homotopy category.
Key Differences Between Module and Ring Spectra
Module spectra are structured as modules over a fixed ring spectrum, emphasizing an external algebraic action, while ring spectra possess an intrinsic multiplication making them algebraic objects internally rich with ring-like structures. The key difference lies in ring spectra having both multiplication and unit maps satisfying associativity and unital conditions, whereas module spectra only require a compatible action of a ring spectrum without necessarily having their own multiplication. This distinction impacts homotopical algebra, where ring spectra enable constructions like smash products and module spectra facilitate the study of ring actions within stable homotopy theory.
Algebraic Structures in Stable Homotopy Theory
Module spectra generalize ring spectra by allowing algebraic operations over a base ring spectrum, forming categories of modules that retain stable homotopy-theoretic structure. Ring spectra provide multiplicative structures that model generalized cohomology theories, serving as foundational objects for constructing module spectra with enriched algebraic properties. The interplay between module spectra and ring spectra underlies the development of algebraic structures such as monoids, algebras, and categories in stable homotopy theory, facilitating advances in understanding derived tensor products and homotopical algebra.
Module Spectrum: Structure and Examples
Module spectra generalize ring spectra by allowing actions over a fixed ring spectrum, preserving structured multiplicative properties while enabling enriched homotopical algebra. The structure of a module spectrum includes a compatible multiplication operation linking the module with the ring spectrum via a homotopy-coherent action map. Common examples include module spectra over the Eilenberg-MacLane spectrum, which correspond to chain complexes of modules over a fixed ring, and module spectra over complex K-theory or cobordism spectra, often used to study generalized cohomology theories.
Ring Spectrum: Definition and Applications
A ring spectrum is a structured spectrum in stable homotopy theory equipped with a multiplication map satisfying associativity and unit axioms up to homotopy, generalizing the concept of a ring to the realm of spectra. It serves as a foundation for defining cohomology theories with multiplicative structures, enabling rich algebraic and geometric applications such as topological K-theory and complex cobordism. Ring spectra facilitate computations in stable homotopy groups and provide frameworks for advanced constructions in derived algebraic geometry and homotopical algebra.
Relationships Between Module and Ring Spectra
Module spectra are structured over ring spectra, where a ring spectrum provides a multiplicative framework enabling the definition of module spectra as objects equipped with an action of the ring spectrum that satisfies associativity and unit conditions. The relationship between a module spectrum and its base ring spectrum parallels classical module theory, with the ring spectrum acting as a base object that governs the algebraic and homotopical properties of the modules. This interaction facilitates constructions such as derived tensor products and homotopy limits, enriching stable homotopy categories with algebraic structures mirroring those in ordinary algebra.
Homotopical Properties of Module vs Ring Spectra
Module spectra exhibit homotopical properties characterized by their structure as stable objects over a fixed ring spectrum, allowing for a more flexible and linear homotopy theory. Ring spectra possess multiplicative structures that induce higher coherences and allow for richer algebraic operations in their homotopy categories, leading to more complex homotopical behavior. The study of module spectra over ring spectra reveals distinguished homotopy limits and colimits, spectral sequences, and derived functors that differentiate their homotopical properties from those of ring spectra themselves.
Notable Constructions: Eilenberg-MacLane and Moore Spectra
The Eilenberg-MacLane spectrum serves as a cornerstone example of a ring spectrum, representing ordinary cohomology with coefficients in an abelian group, while the Moore spectrum exemplifies a module spectrum constructed to realize homology with coefficients in a given module. Eilenberg-MacLane spectra possess strict ring structures corresponding to the cup product in cohomology, enabling algebraic operations within stable homotopy theory. Moore spectra, characterized as modules over these ring spectra, support computations of homology theories with twisted or localized coefficients, illustrating the foundational relationship between ring and module spectra in algebraic topology.
Applications in Algebraic Topology
Module spectra enhance computations in algebraic topology by facilitating structured operations over ring spectra, enabling refined control of cohomology theories and generalized homology theories. Ring spectra serve as foundational building blocks, representing highly structured cohomology theories such as complex cobordism (MU) or topological modular forms (TMF), which are essential for stable homotopy and formal group law computations. The interplay between module spectra and ring spectra allows for the construction of spectral sequences and chromatic filtrations critical to understanding stable homotopy groups and higher algebraic structures.
Recent Advances in Spectra Theory
Recent advances in spectra theory emphasize the enriched structure of module spectra over ring spectra, enhancing the understanding of their stable homotopy categories. Developments in infinity-categories and higher algebra facilitate the construction of module spectra with refined multiplicative structures, enabling new computations in algebraic K-theory and topological modular forms. Innovations in spectral algebraic geometry leverage these module-ring spectrum interactions to classify and manipulate spectral stacks and sheaves more effectively.
Module spectrum Infographic
 libterm.com
libterm.com