A partially ordered group is a mathematical structure where a group is equipped with a partial order that is translation-invariant, meaning the order relation is compatible with the group operation. This concept is fundamental in studying algebraic systems with order properties, enabling applications in areas like lattice theory and ordered algebraic systems. Explore the rest of the article to understand how partially ordered groups influence advanced mathematical theories and your research.
Table of Comparison
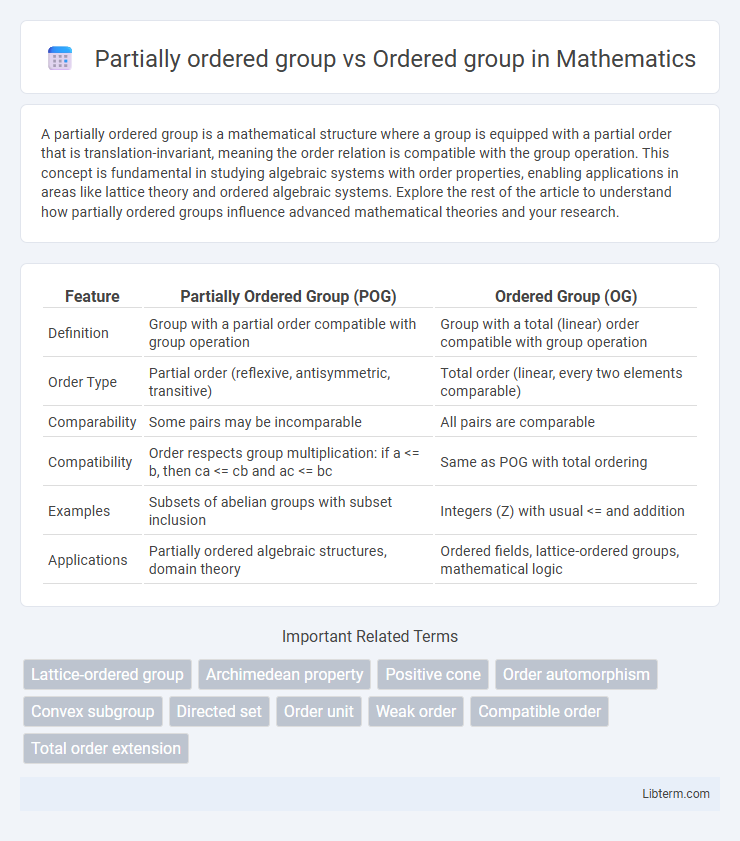
| Feature | Partially Ordered Group (POG) | Ordered Group (OG) |
|---|---|---|
| Definition | Group with a partial order compatible with group operation | Group with a total (linear) order compatible with group operation |
| Order Type | Partial order (reflexive, antisymmetric, transitive) | Total order (linear, every two elements comparable) |
| Comparability | Some pairs may be incomparable | All pairs are comparable |
| Compatibility | Order respects group multiplication: if a <= b, then ca <= cb and ac <= bc | Same as POG with total ordering |
| Examples | Subsets of abelian groups with subset inclusion | Integers (Z) with usual <= and addition |
| Applications | Partially ordered algebraic structures, domain theory | Ordered fields, lattice-ordered groups, mathematical logic |
Introduction to Ordered and Partially Ordered Groups
Ordered groups are algebraic structures equipped with a total order compatible with the group operation, ensuring that for any elements a, b in the group, either a <= b or b <= a holds. Partially ordered groups extend this concept by allowing a partial order, where some elements may be incomparable, maintaining only that the order is translation-invariant under group operations. These structures are fundamental in fields like lattice theory and abstract algebra, providing frameworks to analyze symmetry and order simultaneously.
Defining Ordered Groups
Ordered groups are algebraic structures equipped with a total order compatible with the group operation, meaning the order is translation-invariant and antisymmetric. In contrast, partially ordered groups only require a partial order, which may lack comparability between some elements while still preserving order compatibility with group multiplication. Defining ordered groups involves ensuring a total order that satisfies transitivity, antisymmetry, and totality alongside the group axioms, creating a framework where every pair of elements is comparable under the group order.
Understanding Partially Ordered Groups
Partially ordered groups are algebraic structures equipped with a partial order compatible with the group operation, meaning the order relation is preserved under multiplication. Unlike ordered groups, where the order is total and every pair of elements is comparable, partially ordered groups allow incomparable elements, reflecting more complex hierarchical relationships. Understanding partially ordered groups involves studying how the partial order interacts with group properties, enabling applications in areas like lattice theory and functional analysis.
Key Differences Between Partially Ordered and Ordered Groups
A partially ordered group (po-group) features a binary relation that is reflexive, antisymmetric, and transitive but not necessarily total, allowing some elements to be incomparable, whereas an ordered group requires a total order where every pair of elements is comparable. In a po-group, the order respects the group operation in the sense that if \(a \leq b\), then \(ga \leq gb\) and \(ag \leq bg\) for all \(g\), while an ordered group maintains a linear ordering compatible with group multiplication. Key differences include the presence of comparability in ordered groups and potential gaps in partially ordered groups, impacting algebraic structure analysis and applications in lattice theory and algebraic topology.
Algebraic Structure and Properties
A partially ordered group is an algebraic structure where the group operation is compatible with a partial order, meaning the order relation is reflexive, antisymmetric, and transitive but not necessarily total, allowing some elements to be incomparable. An ordered group, or totally ordered group, strengthens this by requiring a total order compatible with the group operation, ensuring every pair of elements is comparable. Key properties include the translation invariance of the order under the group operation and the requirement that the order respects inverses, making ordered groups integral in studying order-theoretic and algebraic interactions.
Examples of Ordered Groups
Ordered groups are algebraic structures equipped with a total order compatible with the group operation, such as the group of integers (Z, +) with the usual <= relation or the real numbers (R, +) ordered by the standard <=. In contrast, partially ordered groups allow a partial order that may not compare all elements, exemplified by the group of matrices under multiplication with a cone defining the partial order but lacking total comparability. Examples of ordered groups commonly used in mathematics include (Q, +, <=), where every pair of rational numbers is comparable, highlighting the essential distinction from partially ordered groups.
Examples of Partially Ordered Groups
Partially ordered groups generalize ordered groups by allowing the order relation to be a partial order rather than a total order, meaning some elements may be incomparable. Common examples include the group of real-valued functions under pointwise addition with the partial order defined by f <= g if f(x) <= g(x) for all x, and the group of matrices under addition with the Lowner partial order. These examples illustrate how partial orders can capture more complex and nuanced hierarchical structures in algebraic groups beyond the linearity constraints of totally ordered groups.
Applications in Mathematics and Beyond
Partially ordered groups enable modeling of systems where elements have comparability constraints, crucial in lattice theory and domain theory within computer science for semantic analysis. Ordered groups, with total order compatibility, are fundamental in number theory and algebraic topology, supporting the study of divisibility and topological group structures. Both frameworks extend to economics and theoretical physics, where order relations model preference structures and symmetry groups, respectively.
Theoretical Implications and Use Cases
Partially ordered groups allow elements to be compared under a partial order that is compatible with the group operation, enabling analysis in structures where not all elements are comparable, such as lattice-ordered groups and domain theory in computer science. Ordered groups impose a total order compatible with group operations, providing a framework for studying ordered algebraic systems, useful in real number theory, valuation theory, and optimization problems. Theoretical implications include the complexity of ordering relations and applications in algebraic topology, while use cases span from modeling concurrent processes to analyzing monotone transformations in economics.
Conclusion and Comparative Summary
Partially ordered groups have a binary relation that is reflexive, antisymmetric, and transitive but not necessarily total, allowing incomparable elements, while ordered groups require a total order ensuring every pair of elements is comparable. The structural flexibility of partially ordered groups makes them suitable for broader algebraic and order-theoretic applications, whereas ordered groups enable stronger conclusions from total comparability, benefiting fields like lattice theory and ordered algebraic systems. In conclusion, the choice between partially ordered and ordered groups depends on whether the mathematical model prioritizes total comparability or structural generality.
Partially ordered group Infographic
 libterm.com
libterm.com