Etale cohomology provides a powerful tool for studying the properties of algebraic varieties over fields, especially in contexts where classical topology falls short. By employing a sophisticated Grothendieck topology, it allows the definition and computation of cohomology groups that reveal deep arithmetic and geometric information. Dive into the rest of the article to explore how etale cohomology can enrich your understanding of modern algebraic geometry.
Table of Comparison
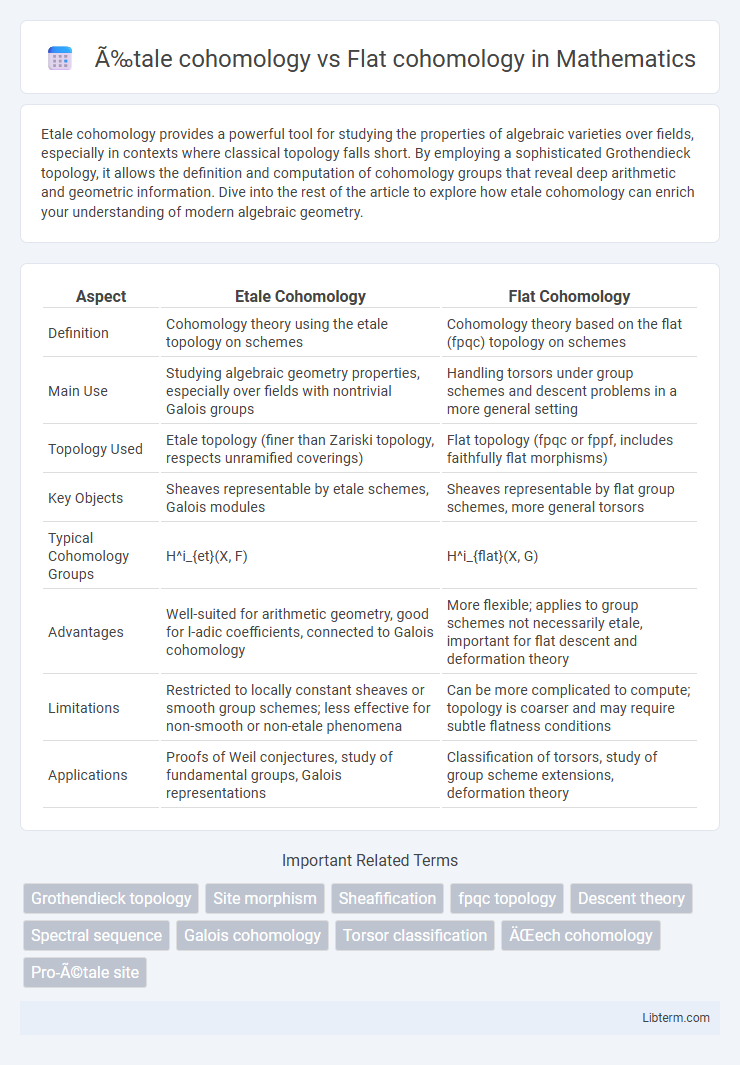
| Aspect | Etale Cohomology | Flat Cohomology |
|---|---|---|
| Definition | Cohomology theory using the etale topology on schemes | Cohomology theory based on the flat (fpqc) topology on schemes |
| Main Use | Studying algebraic geometry properties, especially over fields with nontrivial Galois groups | Handling torsors under group schemes and descent problems in a more general setting |
| Topology Used | Etale topology (finer than Zariski topology, respects unramified coverings) | Flat topology (fpqc or fppf, includes faithfully flat morphisms) |
| Key Objects | Sheaves representable by etale schemes, Galois modules | Sheaves representable by flat group schemes, more general torsors |
| Typical Cohomology Groups | H^i_{et}(X, F) | H^i_{flat}(X, G) |
| Advantages | Well-suited for arithmetic geometry, good for l-adic coefficients, connected to Galois cohomology | More flexible; applies to group schemes not necessarily etale, important for flat descent and deformation theory |
| Limitations | Restricted to locally constant sheaves or smooth group schemes; less effective for non-smooth or non-etale phenomena | Can be more complicated to compute; topology is coarser and may require subtle flatness conditions |
| Applications | Proofs of Weil conjectures, study of fundamental groups, Galois representations | Classification of torsors, study of group scheme extensions, deformation theory |
Introduction to Cohomology Theories in Algebraic Geometry
Etale cohomology provides a powerful tool to study the topology of algebraic varieties over arbitrary fields by using coverings that are locally etale and capturing algebraic analogs of classical topological invariants. Flat cohomology, on the other hand, employs the flat topology, allowing for finer detection of torsors under group schemes and extensions beyond the etale setting, particularly effective for sheaves not representable in the etale site. Both cohomology theories play crucial roles in algebraic geometry by generalizing classical cohomological methods to schemes, enhancing understanding of the arithmetic and geometric properties of algebraic structures.
Basic Concepts of Étale Cohomology
Etale cohomology provides a powerful tool for studying the topological properties of algebraic varieties by using the etale topology, which refines the Zariski topology to incorporate covering spaces defined by etale morphisms. This cohomology theory captures information about the algebraic structure and arithmetic of schemes through etale sheaves and their derived functors, allowing the computation of invariants like the etale fundamental group and algebraic analogues of singular cohomology. Compared to flat cohomology, which deals with torsors and flat morphisms primarily used for descent and deformation problems, etale cohomology excels in applications to number theory and the proof of the Weil conjectures.
Fundamentals of Flat (Fppf) Cohomology
Flat (fppf) cohomology is a Grothendieck topology-based cohomology theory designed to handle sheaves in the faithfully flat, finitely presented topology, making it suitable for studying torsors under group schemes and non-reduced schemes. Unlike etale cohomology, which uses the etale topology and is optimized for smooth and unramified morphisms, flat cohomology excels in capturing finer geometric and algebraic structures, especially related to deformations and infinitesimal extensions. Fundamental concepts include fppf sheaves, covering families defined by faithfully flat morphisms of finite presentation, and the ability to model descent problems and obstructions beyond the scope of etale cohomology.
Key Differences Between Étale and Flat Cohomology
Etale cohomology leverages the etale topology, focusing on unramified morphisms and yielding insights into algebraic varieties over fields, particularly related to Galois representations and l-adic cohomology. Flat cohomology uses the fppf (faithfully flat and finitely presented) topology, capturing finer information about torsors under group schemes, especially useful for studying non-smooth or non-separated group schemes and descent problems. Key differences include the types of covers used (etale morphisms vs. faithfully flat morphisms), the ability of flat cohomology to detect more subtle obstructions related to flat descent, and the broader applicability of flat cohomology in addressing questions about torsors under non-etale or non-finite group schemes.
Advantages and Limitations of Étale Cohomology
Etale cohomology excels in providing powerful tools for studying algebraic varieties over fields with nontrivial Galois groups, offering strong finiteness properties and compatibility with a broad class of coefficients such as l-adic sheaves. Its main advantages include well-behaved functoriality, applicability to schemes of arbitrary dimension, and deep connections to arithmetic geometry via the etale fundamental group. Limitations arise in its complexity for handling torsion phenomena in positive characteristic and insufficient sensitivity to flatness conditions, which flat cohomology addresses more directly by capturing subtle extensions and non-etale phenomena in algebraic geometry.
Strengths and Challenges of Flat Cohomology
Flat cohomology excels in handling torsion phenomena and non-reduced schemes, providing finer invariants in situations where etale cohomology may lose information, especially in positive characteristic or for group schemes not smooth over the base. Its flexibility with non-flat morphisms allows a broader class of algebraic spaces and group schemes to be studied, capturing subtle deformation and extension data beyond the etale topology. However, flat cohomology poses significant computational challenges due to its complex site structure and lack of straightforward comparison theorems, often complicating explicit calculations and limit processes compared to the more established and better-understood etale cohomology framework.
Applications in Number Theory and Algebraic Geometry
Etale cohomology provides powerful tools for studying the arithmetic of algebraic varieties, especially in proving the Weil conjectures and analyzing Galois representations, while flat cohomology excels in classifying torsors under group schemes and handling issues related to descent and deformation theory. In number theory, etale cohomology is fundamental for understanding the behavior of zeta functions and L-series, whereas flat cohomology captures fine arithmetic information about torsion phenomena and integral models of schemes. Algebraic geometers leverage etale cohomology for controlling the etale fundamental group and cohomological dimension, while flat cohomology is instrumental in examining group scheme extensions and obstruction problems in deformation theory.
Comparison of Sheaves: Étale vs. Flat Topologies
Etale cohomology utilizes sheaves defined over the etale topology, capturing information about algebraic varieties through locally isomorphic etale morphisms, while flat cohomology involves sheaves on the flat (fppf) topology, which is finer and based on faithfully flat morphisms. The etale topology is suited for handling torsion phenomena and provides better control over finite etale covers, whereas flat cohomology is more flexible in dealing with infinitesimal extensions and non-reduced schemes. Comparison of etale and flat cohomology sheaves reveals that flat cohomology can detect subtler geometric and arithmetic structures that may escape etale cohomological methods, making it essential for studying deformation problems and descent theory.
Important Theorems and Results for Both Cohomologies
Etale cohomology is fundamentally connected to the Weil conjectures, with Grothendieck's proof relying on its properties such as proper base change, finiteness, and Poincare duality theorems. Flat cohomology is crucial for understanding the classification of torsors and group schemes in algebraic geometry, with results like the fppf cohomological descent and the interpretation of the Brauer group via flat cohomology. The comparison theorems between etale and flat cohomology on smooth schemes reveal deep structural parallels and enable the transfer of cohomological invariants across different topologies.
Choosing the Right Cohomology Theory for Specific Problems
Etale cohomology excels in capturing arithmetic and geometric properties of algebraic varieties over fields with separable extensions, making it ideal for studying problems involving Galois representations and smooth schemes. Flat cohomology is better suited for analyzing torsion phenomena and non-reduced schemes, particularly when dealing with sheaves in the fppf topology or problems involving group schemes and descent theory. Careful selection depends on the nature of the scheme and the cohomological invariants of interest, with etale cohomology preferred for etale-local properties and flat cohomology favored for finer flat-local properties.
Étale cohomology Infographic
 libterm.com
libterm.com