The Vitali set is a fundamental example in measure theory illustrating the existence of non-measurable sets on the real line. Constructed using the axiom of choice, this set challenges conventional notions of length and measure by defying Lebesgue measurability. Discover how the Vitali set reshapes your understanding of mathematical infinity and explore its intriguing properties in the rest of the article.
Table of Comparison
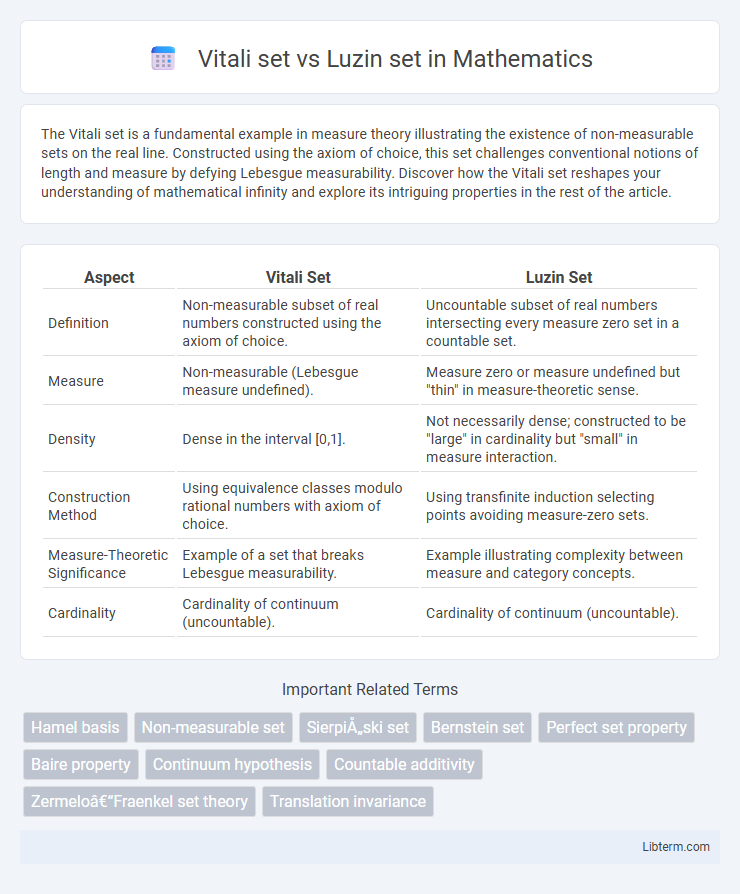
| Aspect | Vitali Set | Luzin Set |
|---|---|---|
| Definition | Non-measurable subset of real numbers constructed using the axiom of choice. | Uncountable subset of real numbers intersecting every measure zero set in a countable set. |
| Measure | Non-measurable (Lebesgue measure undefined). | Measure zero or measure undefined but "thin" in measure-theoretic sense. |
| Density | Dense in the interval [0,1]. | Not necessarily dense; constructed to be "large" in cardinality but "small" in measure interaction. |
| Construction Method | Using equivalence classes modulo rational numbers with axiom of choice. | Using transfinite induction selecting points avoiding measure-zero sets. |
| Measure-Theoretic Significance | Example of a set that breaks Lebesgue measurability. | Example illustrating complexity between measure and category concepts. |
| Cardinality | Cardinality of continuum (uncountable). | Cardinality of continuum (uncountable). |
Introduction to Vitali and Luzin Sets
Vitali sets are constructed using the axiom of choice to create non-measurable subsets of real numbers by selecting exactly one representative from each equivalence class defined by rational translation. Luzin sets are uncountable subsets of real numbers characterized by having countable intersection with every meager set, making them "large" in terms of cardinality but "small" topologically. Both Vitali and Luzin sets illustrate complex interactions between measure theory, topology, and set theory, highlighting the subtleties in defining size and structure within the real line.
Historical Background of Vitali and Luzin Sets
The Vitali set, introduced by Giuseppe Vitali in 1905, marked a significant advance in set theory by providing the first example of a non-measurable set under Lebesgue measure, highlighting limitations in measure theory and the axiom of choice. Luzin sets, named after Nikolai Luzin in the early 20th century, emerged from descriptive set theory and real analysis, focusing on the properties of sets of real numbers related to category and measure. Both sets play seminal roles in the development of modern set theory, illustrating foundational concepts such as measurability, separability, and the interplay between algebraic and topological structures.
Defining the Vitali Set
The Vitali set is a classical example of a non-measurable set constructed using the axiom of choice on the real numbers, specifically by selecting one representative from each equivalence class defined by the relation x ~ y if x - y is rational. In contrast, Luzin sets are uncountable subsets of the real line with strong measure-theoretic properties such as being of measure zero yet ensuring each countable intersection with closed sets is small. The Vitali set challenges Lebesgue measurability by demonstrating the existence of subsets of the real numbers that cannot be assigned a consistent measure.
Properties of the Vitali Set
The Vitali set is a classic example of a non-measurable set constructed using the axiom of choice, characterized by the fact that it contains exactly one representative from each equivalence class defined by rational translations on the real line. Unlike Luzin sets, which are uncountable subsets of the real line with certain measure and category properties, Vitali sets lack Lebesgue measurability and do not have the Baire property. This non-measurability and the absence of a definable structure make the Vitali set a fundamental example illustrating the limitations of measure theory and descriptive set theory in handling arbitrary subsets of the real numbers.
Understanding the Luzin Set
The Luzin set is an uncountable subset of the real numbers characterized by having countable intersections with every measure-zero set, making it a key example in descriptive set theory and measure theory. Unlike the Vitali set, which is non-measurable and constructed using the axiom of choice to create a set without any translation-invariant measure, the Luzin set maintains measurability properties that highlight subtle distinctions between pathological sets. Understanding the Luzin set provides insight into the interactions between measure, category, and the structure of the real line under the continuum hypothesis and other set-theoretic assumptions.
Properties of the Luzin Set
The Luzin set is an uncountable subset of real numbers characterized by each of its countable subsets having measure zero, yet the entire set is of the first category in the Baire space, contrasting with the Vitali set's construction through equivalence classes mod rational numbers. Luzin sets are constructed under the assumption of the Continuum Hypothesis and demonstrate unique category and measure-theoretic properties: they are large in cardinality but "small" in measure and category. These sets highlight intricate interactions between measure, category, and cardinality in descriptive set theory.
Measure Theory: Vitali Set vs Luzin Set
The Vitali set demonstrates the existence of non-measurable subsets of real numbers under Lebesgue measure, constructed using the axiom of choice to select representatives from equivalence classes modulo rational numbers. In contrast, Luzin sets are subsets of the real line that are uncountable, yet intersect every measure zero set in at most countably many points, illustrating subtle interactions between measure and category. Both sets underscore fundamental limitations in measure theory, with the Vitali set highlighting non-measurability and the Luzin set exemplifying complex measure-category duality.
Implications in Real Analysis
Vitali sets and Luzin sets illustrate key concepts regarding non-measurable sets and measure theory in real analysis, revealing limitations of Lebesgue measure and the axiom of choice. Vitali sets exemplify the existence of subsets of real numbers that are not Lebesgue measurable, challenging the classical understanding of measure and integration. Luzin sets, constructed under the continuum hypothesis, highlight properties of uncountable subsets of reals with strong measure-category duality implications, deepening insights into Borel hierarchy and descriptive set theory.
Key Differences between Vitali and Luzin Sets
Vitali sets are non-measurable subsets of real numbers constructed using the axiom of choice, characterized by their ability to demonstrate the existence of sets without Lebesgue measure, while Luzin sets are uncountable subsets of real numbers with measure zero yet dense in a particular sense. Key differences include Vitali sets lacking measure entirely and relying explicitly on equivalence classes modulo rational numbers, whereas Luzin sets contain no perfect subsets and emphasize descriptive set theory properties within the continuum. The construction of Vitali sets highlights non-measurability and the failure of countable additivity, whereas Luzin sets focus on measure-zero density and avoidance of perfect sets, underpinning their distinct roles in real analysis and set theory.
Applications and Significance in Modern Mathematics
Vitali sets and Luzin sets illustrate fundamental concepts in measure theory and set theory, with Vitali sets demonstrating the existence of non-measurable sets under the axiom of choice, impacting the study of real analysis and probability theory. Luzin sets, as uncountable subsets of the real line with strong category properties, play a crucial role in descriptive set theory and the analysis of Baire category, influencing topology and functional analysis. These sets highlight limitations of classical measures and categories, guiding advancements in understanding pathological examples and the structure of real numbers.
Vitali set Infographic
 libterm.com
libterm.com