Reductive thinking often oversimplifies complex issues, stripping away important nuances that contribute to a full understanding. This approach can lead to misinterpretations and ineffective solutions, especially in fields requiring detailed analysis. Explore the rest of the article to uncover how reductive reasoning impacts decision-making and how you can adopt more comprehensive strategies.
Table of Comparison
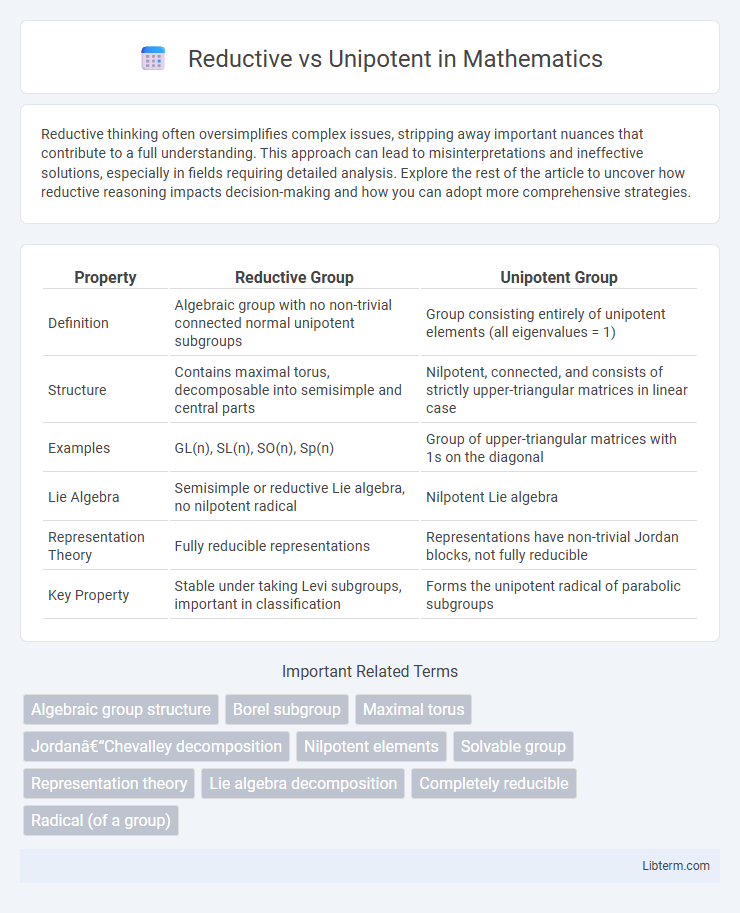
| Property | Reductive Group | Unipotent Group |
|---|---|---|
| Definition | Algebraic group with no non-trivial connected normal unipotent subgroups | Group consisting entirely of unipotent elements (all eigenvalues = 1) |
| Structure | Contains maximal torus, decomposable into semisimple and central parts | Nilpotent, connected, and consists of strictly upper-triangular matrices in linear case |
| Examples | GL(n), SL(n), SO(n), Sp(n) | Group of upper-triangular matrices with 1s on the diagonal |
| Lie Algebra | Semisimple or reductive Lie algebra, no nilpotent radical | Nilpotent Lie algebra |
| Representation Theory | Fully reducible representations | Representations have non-trivial Jordan blocks, not fully reducible |
| Key Property | Stable under taking Levi subgroups, important in classification | Forms the unipotent radical of parabolic subgroups |
Introduction to Reductive and Unipotent Concepts
Reductive groups are algebraic groups characterized by the absence of nontrivial connected unipotent normal subgroups, playing a crucial role in representation theory and algebraic geometry. Unipotent groups consist solely of unipotent elements, where each element's eigenvalues are all equal to one, and these groups often appear as normal subgroups within larger algebraic structures. The distinction between reductive and unipotent groups underlies the structural decomposition of linear algebraic groups into semisimple and solvable components.
Defining Reductive Groups
Reductive groups are algebraic groups characterized by the property that their unipotent radical is trivial, meaning they contain no nontrivial connected normal unipotent subgroups. This contrasts with unipotent groups, which are entirely composed of unipotent elements and lack semisimple components. In representation theory, reductive groups play a crucial role due to their semisimple Lie algebras and well-behaved module categories.
Understanding Unipotent Elements
Unipotent elements in linear algebraic groups are defined by having all eigenvalues equal to one, which distinguishes them from reductive elements characterized by diagonalizable action with eigenvalues other than one. Understanding unipotent elements involves studying their nilpotent behavior in conjugation, facilitating the analysis of group structure via Jordan decomposition. These elements play a crucial role in the representation theory of algebraic groups and influence the classification of algebraic group actions and varieties.
Key Differences Between Reductive and Unipotent
Reductive groups are algebraic groups characterized by their semisimple structure with no nontrivial connected normal unipotent subgroups, whereas unipotent groups consist entirely of unipotent elements, meaning every group element has all eigenvalues equal to one. Key differences include that reductive groups generalize semisimple groups by allowing a central torus and play a central role in representation theory due to their well-behaved module categories, while unipotent groups are nilpotent, often simpler in structure but lacking semisimplicity. Reductive groups have stable decompositions into maximal tori and semisimple parts, contrasting with unipotent groups where every element behaves like a nilpotent transformation, impacting the nature of their algebraic actions and invariant theory.
Historical Background and Significance
Reductive groups, emerging from the classification of algebraic groups in the early 20th century, are fundamental objects in modern representation theory and algebraic geometry due to their well-behaved structure and maximal tori. Unipotent groups, characterized by all elements being unipotent matrices, trace back to studies in Lie theory and play a crucial role in understanding nilpotent elements and the decomposition of algebraic groups. The distinction between reductive and unipotent groups underpins significant advances in the theory of algebraic groups, influencing the development of geometric representation theory and the Langlands program.
Algebraic Structures: Reductive vs Unipotent
Reductive algebraic groups are characterized by their semisimple representation theory and the absence of nontrivial connected normal unipotent subgroups, making them stable under conjugation and central to the structure theory of algebraic groups. Unipotent groups consist entirely of unipotent elements, which are elements whose minus identity is nilpotent; these groups often appear as normal subgroups representing radical components in solvable or parabolic subgroups. The contrast in algebraic structures highlights reductive groups' decomposability into tori and semisimple groups, while unipotent groups exhibit a nilpotent Lie algebra structure crucial for understanding group actions and geometric properties.
Applications in Representation Theory
Reductive groups, characterized by well-behaved representation categories and complete reducibility, play a central role in representation theory due to their rich structure and classification of irreducible representations, particularly in Lie theory and algebraic groups. Unipotent groups, whose elements have all eigenvalues equal to one, exhibit more intricate and less understood representation behavior, often requiring specialized methods such as orbit method or cohomological techniques to analyze their representations. Applications of reductive groups include the study of symmetries in physics and number theory through Langlands program, while unipotent groups find applications in nilpotent orbits classification and deformation theory.
Examples from Classic Algebraic Groups
Reductive algebraic groups, such as GL_n (general linear groups) and SL_n (special linear groups), feature semisimple structures with no nontrivial connected normal unipotent subgroups, exemplifying stability under conjugation. In contrast, unipotent groups, like the subgroup of upper triangular matrices with ones on the diagonal within GL_n, consist entirely of elements whose eigenvalues are all one, emphasizing their nilpotent action on vector spaces. The distinction between reductive and unipotent groups is foundational in the classification of algebraic groups and their representations.
Implications in Modern Mathematical Research
Reductive and unipotent groups play pivotal roles in modern mathematical research, particularly in algebraic geometry and representation theory. Reductive groups, characterized by their well-behaved representation categories and semisimple structure, enable deep insights into symmetry and invariant theory. Unipotent groups, defined by nilpotent elements and a more intricate structure, contribute to understanding geometric properties of algebraic varieties and deformation theory, highlighting their complementary implications in advanced mathematical frameworks.
Conclusion: Choosing Between Reductive and Unipotent
Choosing between reductive and unipotent groups depends heavily on the specific properties required in algebraic group theory applications. Reductive groups feature semisimple representation theories and lack nontrivial connected normal unipotent subgroups, making them ideal for simplifying structural analysis. In contrast, unipotent groups, characterized by all elements having only eigenvalue one, are crucial for understanding nilpotent actions and upper-triangular matrix behaviors in Lie theory.
Reductive Infographic
 libterm.com
libterm.com