Spin structure is a fundamental concept in differential geometry and theoretical physics, providing a framework for defining spinor fields on a manifold. It enables the extension of classical geometric methods to incorporate quantum properties of particles with half-integer spin, crucial for understanding fermions in quantum field theory. Explore the rest of the article to discover how spin structures impact modern physics and geometry in detail.
Table of Comparison
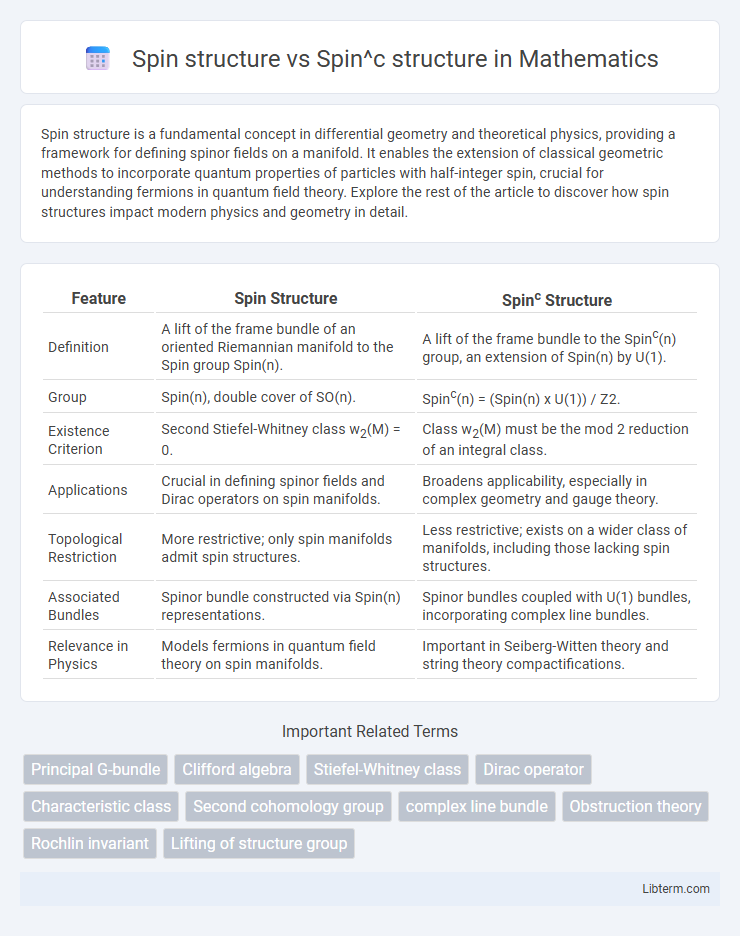
| Feature | Spin Structure | Spinc Structure |
|---|---|---|
| Definition | A lift of the frame bundle of an oriented Riemannian manifold to the Spin group Spin(n). | A lift of the frame bundle to the Spinc(n) group, an extension of Spin(n) by U(1). |
| Group | Spin(n), double cover of SO(n). | Spinc(n) = (Spin(n) x U(1)) / Z2. |
| Existence Criterion | Second Stiefel-Whitney class w2(M) = 0. | Class w2(M) must be the mod 2 reduction of an integral class. |
| Applications | Crucial in defining spinor fields and Dirac operators on spin manifolds. | Broadens applicability, especially in complex geometry and gauge theory. |
| Topological Restriction | More restrictive; only spin manifolds admit spin structures. | Less restrictive; exists on a wider class of manifolds, including those lacking spin structures. |
| Associated Bundles | Spinor bundle constructed via Spin(n) representations. | Spinor bundles coupled with U(1) bundles, incorporating complex line bundles. |
| Relevance in Physics | Models fermions in quantum field theory on spin manifolds. | Important in Seiberg-Witten theory and string theory compactifications. |
Introduction to Spin and Spin^c Structures
Spin structures provide a framework for defining spinor fields on oriented Riemannian manifolds, enabling the lifting of the frame bundle from the special orthogonal group SO(n) to its double cover Spin(n). Spin^c structures extend this concept by incorporating a U(1) bundle to address manifolds where Spin structures may not exist, allowing for a broader class of manifolds to admit spinor fields twisted by complex line bundles. These structures play a crucial role in geometry and topology, particularly in the study of Dirac operators and index theory.
Mathematical Background: Manifolds and Bundles
Spin structures and Spin^c structures arise in the study of smooth manifolds equipped with tangent bundles, serving as refinements of the frame bundle's structure group reduction. A Spin structure corresponds to a lift of the principal SO(n)-bundle (frame bundle) of an oriented Riemannian manifold to the spin group Spin(n), existing only when the second Stiefel-Whitney class w_2 of the manifold vanishes. Spin^c structures generalize Spin structures by allowing a further U(1)-bundle twist, characterized by combining the spin group with the circle group U(1), thus existing on manifolds where w_2 may be nontrivial but with a particular cohomological constraint involving a class in H^2(M;Z).
What is a Spin Structure?
A Spin structure is a mathematical framework that lifts the frame bundle of an oriented Riemannian manifold to its Spin group, enabling the definition of spinor fields essential in quantum field theory and differential geometry. It exists only on manifolds whose second Stiefel-Whitney class vanishes, ensuring orientability and the ability to consistently define spinors. This structure serves as a prerequisite for defining a Spin^c structure, which generalizes Spin structures to accommodate manifolds with nontrivial second Stiefel-Whitney classes by incorporating an additional U(1) bundle.
Defining Spin^c Structures
Spin^c structures extend Spin structures by incorporating an additional U(1) gauge symmetry, allowing the definition of spinors on manifolds that lack a Spin structure. A Spin^c structure on an oriented Riemannian manifold is a lift of the principal SO(n)-bundle to a principal Spin^c(n)-bundle, where Spin^c(n) is the group Spin(n) x_{Z2} U(1). This framework facilitates the construction of Dirac operators and the study of index theory on a broader class of manifolds, especially those with nontrivial second Stiefel-Whitney class.
Key Differences Between Spin and Spin^c Structures
Spin structures are special lifts of the frame bundle of an oriented Riemannian manifold to the Spin group, enabling the definition of spinor fields and facilitating the formulation of fermionic fields in physics, particularly in quantum field theory. Spin^c structures generalize Spin structures by incorporating an additional U(1) bundle, allowing their existence on a broader class of manifolds where spin structures may not exist, such as non-spin manifolds with nontrivial second Stiefel-Whitney classes. Key differences include the topological constraints: Spin structures require vanishing second Stiefel-Whitney class (w_2=0), while Spin^c structures only require the vanishing of the third integral Stiefel-Whitney class (W_3), thus providing more flexibility in geometric and topological applications.
Topological Obstructions and Existence Criteria
Spin structures require the second Stiefel-Whitney class \( w_2 \) of the tangent bundle to vanish, representing a topological obstruction to their existence on a manifold. Spin\(^c\) structures generalize Spin structures by combining the tangent bundle with a complex line bundle, allowing their existence when \( w_2 \) is the mod 2 reduction of the first Chern class \( c_1 \), thereby relaxing topological constraints. The existence criterion for Spin structures is \( w_2 = 0 \), while Spin\(^c\) structures exist if there is a class \( c_1 \in H^2(M, \mathbb{Z}) \) such that \( w_2 = c_1 \mod 2 \).
Physical Interpretations and Applications
Spin structures provide a mathematical framework for defining spinors on orientable manifolds, crucial for formulating fermionic fields in quantum field theory and general relativity. Spin^c structures extend this concept by incorporating an additional U(1) gauge field, enabling the description of charged fermions and allowing the analysis of anomalies and topological insulators in condensed matter physics. These structures facilitate bridging geometry with physical theories, particularly in understanding Dirac operators, supersymmetry, and string theory compactifications.
Relationship to Clifford Algebras
Spin structures arise as lifts of the frame bundle to the Spin group, associated with Clifford algebras generated by vector spaces with quadratic forms, providing a double cover of the special orthogonal group SO(n). Spin^c structures extend Spin structures by incorporating an additional U(1) factor, linked to complex Clifford algebras and the group Spin^c(n) = (Spin(n) x U(1))/Z_2, enabling constructions on manifolds lacking Spin structures but admitting Spin^c structures. The relationship to Clifford algebras is fundamental, as Spin corresponds to the even subalgebra of real Clifford algebras Cl_n, while Spin^c involves the complexified Clifford algebras Cl_n C, reflecting the interplay between real and complex representations in geometry and topology.
Examples in Geometry and Physics
Spin structures offer a method to define spinor fields on oriented Riemannian manifolds, crucial in modeling fermions in quantum field theory, whereas Spin^c structures generalize this notion, allowing topological obstructions to be circumvented by incorporating an additional U(1) bundle. In geometry, Spin structures exist on manifolds with vanishing second Stiefel-Whitney class, such as simply connected 3-dimensional spheres, while Spin^c structures appear more broadly, for example on complex projective spaces CP^n, enabling the definition of Dirac operators where pure Spin structures fail. In physics, Spin^c structures provide the mathematical framework necessary for analyzing systems with both spin and electromagnetic fields, playing a pivotal role in Seiberg-Witten theory and the study of topological insulators, whereas Spin structures underlie fundamental models of relativistic fermions in spaces like Minkowski spacetime.
Summary and Further Reading
Spin structures provide a framework for defining spinors on manifolds, requiring the second Stiefel-Whitney class to vanish, thus allowing lift of the frame bundle to a Spin group. Spin^c structures generalize spin structures by incorporating an additional U(1) bundle, relaxing the topological constraints and enabling applications on a broader class of manifolds where spin structures may not exist. For further reading, consult "Spin Geometry" by Lawson and Michelsohn and the survey paper "Spin^c Structures and Dirac Operators on Manifolds" for comprehensive insights and advanced mathematical treatments.
Spin structure Infographic
 libterm.com
libterm.com