Baire space is a topological space fundamental in descriptive set theory and analysis, characterized by being homeomorphic to the set of all sequences of natural numbers with the product topology. It exhibits the Baire category property, meaning the intersection of countably many dense open sets is dense, which has important implications in functional analysis and topology. Explore the rest of this article to understand how Baire space influences various mathematical fields and why it matters for your studies.
Table of Comparison
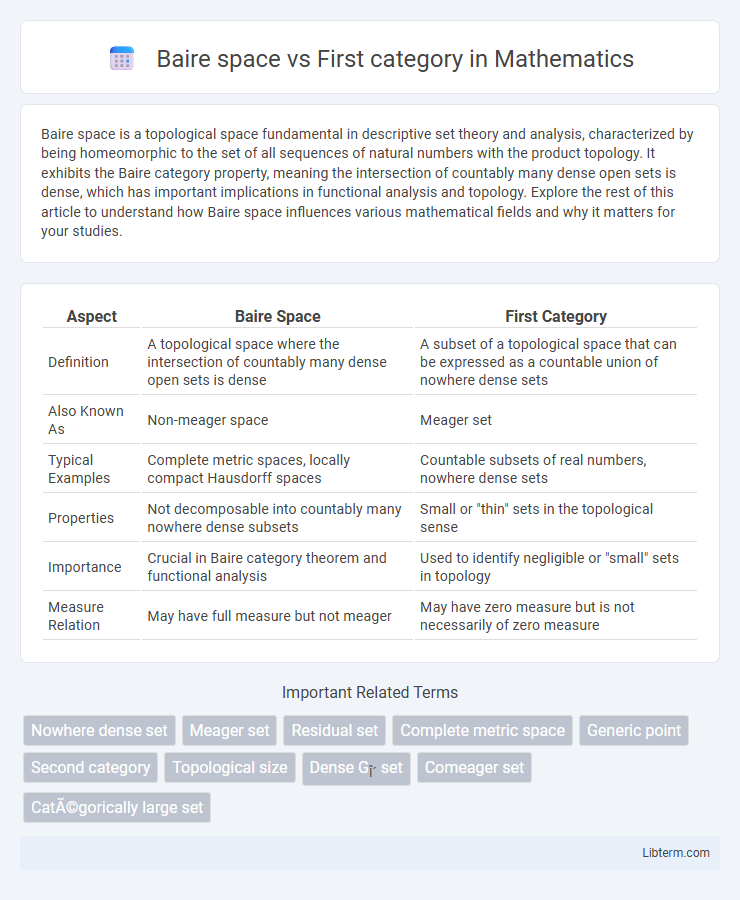
| Aspect | Baire Space | First Category |
|---|---|---|
| Definition | A topological space where the intersection of countably many dense open sets is dense | A subset of a topological space that can be expressed as a countable union of nowhere dense sets |
| Also Known As | Non-meager space | Meager set |
| Typical Examples | Complete metric spaces, locally compact Hausdorff spaces | Countable subsets of real numbers, nowhere dense sets |
| Properties | Not decomposable into countably many nowhere dense subsets | Small or "thin" sets in the topological sense |
| Importance | Crucial in Baire category theorem and functional analysis | Used to identify negligible or "small" sets in topology |
| Measure Relation | May have full measure but not meager | May have zero measure but is not necessarily of zero measure |
Understanding Baire Space: Key Concepts
Baire space is a topological space where the countable intersection of open dense sets is dense, highlighting its robustness against "thin" or negligible subsets. First category sets, also known as meager sets, are those that can be expressed as a countable union of nowhere dense subsets, contrasting with Baire spaces that cannot be decomposed entirely into such "small" sets. This distinction is crucial in functional analysis and topology, ensuring that Baire spaces maintain a rich, nontrivial structure despite the presence of first category subsets.
Defining First Category Sets
First category sets, also known as meager sets, are defined as countable unions of nowhere dense subsets within a topological space, such as a Baire space. In a Baire space, the complement of a first category set is dense, implying that first category sets are "small" or "negligible" in terms of topological size. The distinction between first category and non-first category sets helps characterize the structure of Baire spaces, crucial for understanding typical properties in functional analysis and topology.
Distinctions Between Baire Space and First Category
Baire space is a topological space where the intersection of countably many dense open sets is dense, ensuring it is not of first category (meager). First category spaces, also known as meager spaces, can be expressed as the countable union of nowhere dense subsets, indicating a "small" or "thin" topological structure. The key distinction lies in the robustness of Baire spaces against meagerness, which guarantees the presence of "large" or "typical" subsets, unlike first category spaces that are considered topologically "insignificant.
Topological Implications of Baire Spaces
Baire spaces guarantee that the countable intersection of dense open sets remains dense, preventing the space from being expressed as a countable union of nowhere dense sets, or first category sets. This property ensures robustness in topological structures, supporting the validity of the Baire Category Theorem and enabling critical applications in functional analysis and topology. Consequently, Baire spaces play a pivotal role in distinguishing "large" or "typical" subsets from meager or of first category subsets within a given topological framework.
Dense and Nowhere Dense Sets Explained
Baire space is a topological space where the intersection of countably many dense open sets remains dense, ensuring it is not of first category, meaning it cannot be expressed as a countable union of nowhere dense sets. Dense sets in Baire spaces contain points arbitrarily close to every point in the space, whereas nowhere dense sets have closures with empty interiors, making them "small" in a topological sense. The distinction between dense and nowhere dense sets is fundamental in characterizing Baire spaces and understanding the structure of first category sets, which are considered "topologically meager.
Baire Category Theorem Overview
The Baire Category Theorem states that in a complete metric space or a locally compact Hausdorff space, the intersection of countably many dense open sets is dense, ensuring the space is a Baire space. First category sets, also known as meager sets, are countable unions of nowhere dense sets and represent "small" or "negligible" subsets in the context of topology. The theorem distinguishes spaces where these meager sets do not contain an open subset, emphasizing the robustness of Baire spaces against such sparse configurations.
Examples of Baire Spaces in Mathematics
Baire spaces include complete metric spaces, locally compact Hausdorff spaces, and the space of irrational numbers with the usual topology. These spaces are characterized by the property that countable intersections of dense open sets remain dense, contrasting first category spaces, which can be expressed as countable unions of nowhere dense sets. Prominent examples illustrating Baire category concepts include Banach spaces and the real line with the usual metric topology.
Real-World Applications of First Category Sets
First category sets, also known as meager sets, play a crucial role in functional analysis and dynamical systems by identifying "small" or negligible subsets within Baire spaces, which are complete metric spaces like the real numbers. These sets aid in understanding stability and generic properties of solutions to differential equations, informing the design of stable control systems and signal processing algorithms. The concept of first category sets also supports complexity analysis in computer science, isolating exceptional or rare scenarios that do not affect the overall system behavior in practical applications.
Baire Space vs First Category: Common Misconceptions
Baire spaces are topological spaces where the intersection of countably many dense open sets remains dense, whereas first category sets, also called meager sets, are those that can be expressed as a countable union of nowhere dense sets. A common misconception is that every subset of a Baire space is non-meager, but many important subsets can be first category despite residing in a Baire space. Understanding the distinction helps clarify that Baire spaces provide a robust setting for typical behaviors in topology, while first category sets represent "small" or "negligible" parts within those spaces.
Conclusion: Insights and Comparative Summary
Baire space, characterized by the property that the countable intersection of dense open sets is dense, contrasts sharply with first category (meager) sets, which are countable unions of nowhere dense sets and represent "small" or "negligible" subsets in topological spaces. This distinction underscores that while Baire spaces preserve largeness and density through typical set operations, first category sets indicate topological "thinness" and rarity. Understanding this dichotomy is crucial for analyzing the structural robustness of function spaces and continuity properties in real analysis and topology.
Baire space Infographic
 libterm.com
libterm.com