Elliptic is a leading blockchain analytics company specializing in cryptocurrency compliance and risk management solutions. Their technology helps financial institutions, law enforcement, and enterprises trace illicit activities and ensure regulatory adherence in digital asset transactions. Explore this article to discover how Elliptic can safeguard your crypto operations and enhance security.
Table of Comparison
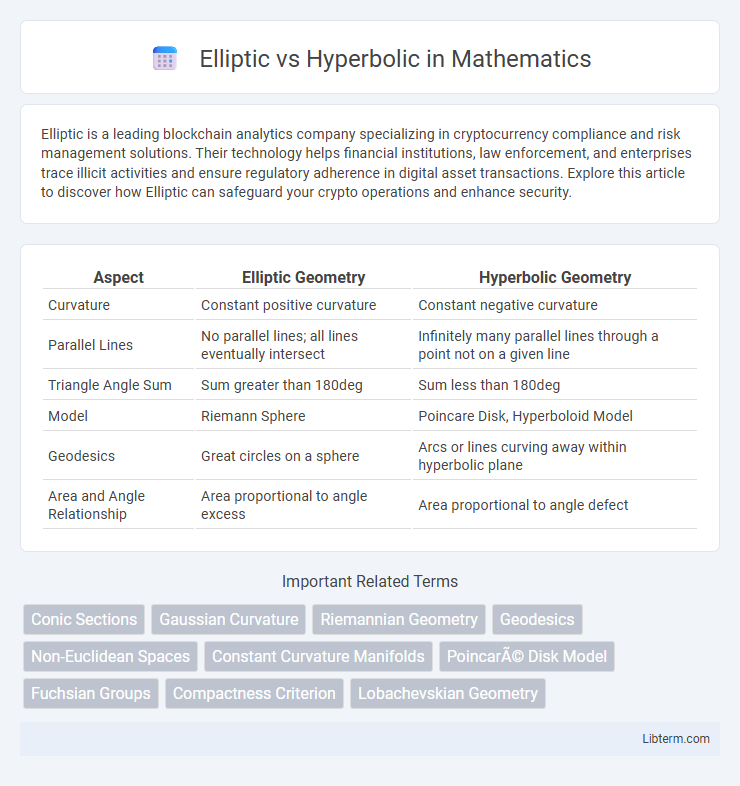
| Aspect | Elliptic Geometry | Hyperbolic Geometry |
|---|---|---|
| Curvature | Constant positive curvature | Constant negative curvature |
| Parallel Lines | No parallel lines; all lines eventually intersect | Infinitely many parallel lines through a point not on a given line |
| Triangle Angle Sum | Sum greater than 180deg | Sum less than 180deg |
| Model | Riemann Sphere | Poincare Disk, Hyperboloid Model |
| Geodesics | Great circles on a sphere | Arcs or lines curving away within hyperbolic plane |
| Area and Angle Relationship | Area proportional to angle excess | Area proportional to angle defect |
Introduction: Understanding Elliptic and Hyperbolic Concepts
Elliptic and hyperbolic geometries represent two distinct types of non-Euclidean geometry, characterized by different curvature properties: elliptic geometry features constant positive curvature while hyperbolic geometry exhibits constant negative curvature. These concepts play crucial roles in various mathematical fields, including differential geometry, complex analysis, and theoretical physics, especially in the study of spacetime models and cosmology. Understanding the fundamental differences between elliptic and hyperbolic spaces aids in grasping the behavior of geodesics, angles, and parallel lines unique to each geometry.
Defining Elliptic Geometry
Elliptic geometry is defined by a surface where straight lines curve inward, resembling the geometry on a sphere, with no parallel lines existing because all great circles eventually intersect. Unlike hyperbolic geometry, which features saddle-shaped curvature and infinite parallel lines through a point, elliptic geometry exhibits positive curvature and finite area. Key properties include triangle angle sums greater than 180 degrees and the absence of boundary, distinguishing it in non-Euclidean geometry.
Exploring Hyperbolic Geometry
Hyperbolic geometry, characterized by a constant negative curvature, contrasts sharply with elliptic geometry's positive curvature, creating unique properties such as the divergence of parallel lines and exponential area growth. This non-Euclidean geometry finds applications in complex analysis, cosmology, and network theory, where traditional Euclidean assumptions fail to model real-world phenomena accurately. Understanding hyperbolic geometry enhances insights into spaces with saddle-like structures and provides tools for visualizing and analyzing large-scale geometric and topological behaviors.
Key Differences Between Elliptic and Hyperbolic Structures
Elliptic structures feature positive curvature, leading to closed and finite geometries such as spheres, while hyperbolic structures exhibit negative curvature, creating open and infinite geometries exemplified by saddle-shaped surfaces. The metric properties differ significantly, with elliptic geometry lacking parallel lines and hyperbolic geometry possessing infinitely many parallels through a point not on a given line. Elliptic spaces are characterized by finite area and volume constraints, contrasting the expansive growth and exponential area increase found in hyperbolic spaces.
Applications in Mathematics and Physics
Elliptic equations, such as Laplace's equation, are fundamental in steady-state heat conduction, electrostatics, and gravitational potentials, providing solutions that describe equilibrium states. Hyperbolic equations, exemplified by the wave equation, model dynamic phenomena including sound propagation, electromagnetic waves, and fluid dynamics, capturing time-dependent behaviors and signal transmission. In mathematical physics, elliptic operators characterize boundary value problems, while hyperbolic operators govern initial value problems, crucial for understanding stability and evolution in physical systems.
Real-World Examples of Elliptic Geometry
Elliptic geometry is exemplified in real-world applications such as the surface of the Earth, where the shortest path between two points follows great circles rather than straight lines. This geometric model is crucial in global navigation systems, including airline route optimization and GPS technology, which rely on curved space representations. Unlike hyperbolic geometry, elliptic geometry governs closed surfaces with positive curvature, making it integral to fields like astronomy and geodesy.
Real-World Implementations of Hyperbolic Geometry
Hyperbolic geometry underpins models of complex networks and hierarchical structures in computer science, enabling efficient data organization and visualization techniques such as hyperbolic trees. In physics, it informs the study of spacetime in cosmology, particularly in models of the universe with negative curvature consistent with Einstein's field equations. Unlike elliptic geometry, which is applied in spherical contexts like global positioning and geodesy, hyperbolic geometry supports non-Euclidean spatial representations essential for advancements in network theory and theoretical physics.
Visual Representations: Comparing Geometric Models
Elliptic geometry is visually represented through spherical models where straight lines correspond to great circles, creating closed and finite spaces with no parallel lines. Hyperbolic geometry uses saddle-shaped models like the Poincare disk or the hyperboloid, illustrating infinite planes where lines curve away and multiple parallels can diverge from a single point. These contrasting visual models highlight the fundamental differences in curvature and parallelism between elliptic and hyperbolic geometries.
Historical Development of Elliptic and Hyperbolic Theories
Elliptic and hyperbolic geometries trace their origins to the 19th century when mathematicians sought alternatives to Euclidean geometry's parallel postulate. Carl Friedrich Gauss, Nikolai Lobachevsky, and Janos Bolyai independently developed hyperbolic geometry by rejecting the parallel postulate, while Bernhard Riemann established elliptic geometry through his work on curved surfaces and the concept of Riemannian manifolds. These groundbreaking theories revolutionized the understanding of space, influencing modern physics and topology.
Conclusion: Choosing Between Elliptic and Hyperbolic Approaches
Elliptic approaches excel in modeling smooth, closed surfaces with stable boundary conditions, ideal for applications requiring precise control and finite domains. Hyperbolic methods are better suited for dynamic systems involving wave propagation and open, unbounded domains where rapid signal transmission is critical. Choosing between elliptic and hyperbolic approaches depends on the problem's nature--elliptic for equilibrium states and boundary value problems, hyperbolic for time-dependent processes and hyperbolic partial differential equations.
Elliptic Infographic
 libterm.com
libterm.com