The outer product is a mathematical operation that takes two vectors and produces a matrix, where each element is the product of elements from the corresponding positions in the vectors. This operation is crucial in fields like linear algebra, machine learning, and quantum computing for creating higher-dimensional representations from lower-dimensional data. Explore the rest of the article to understand how the outer product can enhance your computations and applications.
Table of Comparison
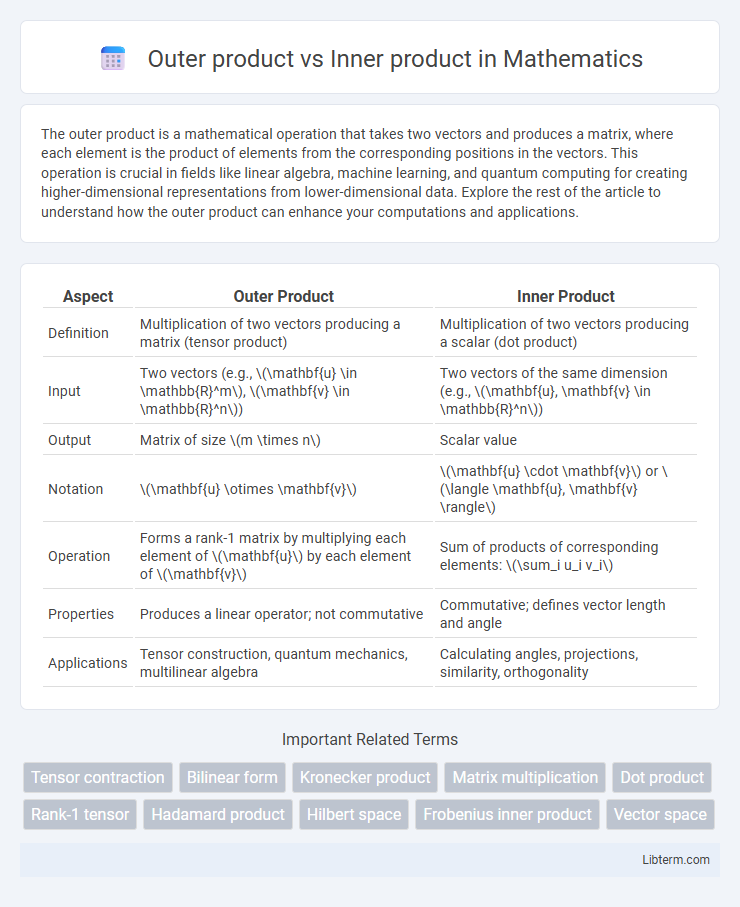
| Aspect | Outer Product | Inner Product |
|---|---|---|
| Definition | Multiplication of two vectors producing a matrix (tensor product) | Multiplication of two vectors producing a scalar (dot product) |
| Input | Two vectors (e.g., \(\mathbf{u} \in \mathbb{R}^m\), \(\mathbf{v} \in \mathbb{R}^n\)) | Two vectors of the same dimension (e.g., \(\mathbf{u}, \mathbf{v} \in \mathbb{R}^n\)) |
| Output | Matrix of size \(m \times n\) | Scalar value |
| Notation | \(\mathbf{u} \otimes \mathbf{v}\) | \(\mathbf{u} \cdot \mathbf{v}\) or \(\langle \mathbf{u}, \mathbf{v} \rangle\) |
| Operation | Forms a rank-1 matrix by multiplying each element of \(\mathbf{u}\) by each element of \(\mathbf{v}\) | Sum of products of corresponding elements: \(\sum_i u_i v_i\) |
| Properties | Produces a linear operator; not commutative | Commutative; defines vector length and angle |
| Applications | Tensor construction, quantum mechanics, multilinear algebra | Calculating angles, projections, similarity, orthogonality |
Introduction to Inner and Outer Products
The inner product is a scalar value representing the projection of one vector onto another, calculated by summing the products of their corresponding components, and it is fundamental in defining vector length and angles. The outer product, in contrast, produces a matrix by multiplying a column vector by a row vector, enabling the construction of linear transformations and capturing directionality in higher dimensions. Both products are essential in linear algebra, with the inner product emphasizing magnitude alignment and the outer product emphasizing tensor formation.
Defining the Inner Product
The inner product is a scalar value obtained by multiplying corresponding components of two vectors and summing the results, defined as
Understanding the Outer Product
The outer product of two vectors produces a matrix, representing all pairwise multiplications between elements of the first vector (column vector) and the second vector (row vector), which is essential in tensor construction and feature interactions. Unlike the inner product that results in a scalar by summing element-wise multiplications, the outer product preserves dimensional relationships and reveals directional dependencies. This operation is fundamental in applications such as quantum mechanics, machine learning for constructing rank-1 matrices, and feature mapping in kernel methods.
Mathematical Notation and Formulas
The inner product, denoted as \(\mathbf{a} \cdot \mathbf{b}\) or \(\langle \mathbf{a}, \mathbf{b} \rangle\), is a scalar defined by \(\sum_{i=1}^n a_i b_i\) for vectors \(\mathbf{a}, \mathbf{b} \in \mathbb{R}^n\). The outer product, represented as \(\mathbf{a} \otimes \mathbf{b}\) or \(\mathbf{a} \mathbf{b}^T\), yields an \(n \times m\) matrix with elements \(a_i b_j\) for \(\mathbf{a} \in \mathbb{R}^n\) and \(\mathbf{b} \in \mathbb{R}^m\). Inner products map \(\mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}\), while outer products map \(\mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^{n \times m}\).
Geometric Interpretation
The inner product, also known as the dot product, represents the projection of one vector onto another, quantifying the cosine of the angle between them and yielding a scalar that reflects their directional alignment. In contrast, the outer product generates a matrix capturing the linear transformation defined by two vectors, geometrically representing an oriented area (or volume in higher dimensions) spanned by these vectors. While the inner product measures similarity and angle, the outer product encodes the multidimensional space defined by vector interactions.
Applications in Linear Algebra
The outer product generates a matrix from two vectors, crucial for constructing rank-1 matrices and tensor decompositions in linear algebra, enhancing dimensionality reduction and data compression techniques. The inner product calculates a scalar representing vector similarity or projection magnitude, widely used in orthogonality tests, vector norms, and solving systems of linear equations. Both products underpin eigenvalue computations, matrix factorization methods, and transformations in machine learning and signal processing.
Differences Between Inner and Outer Products
The inner product, also known as the dot product, results in a scalar value by multiplying corresponding elements of two vectors and summing the results, primarily measuring vector similarity or projection. In contrast, the outer product produces a matrix by multiplying each element of one vector by every element of another, capturing the pairwise interactions between vector components. The core difference lies in their output types and applications: inner product yields a scalar focusing on magnitude relations, while outer product generates a higher-dimensional matrix useful in tensor decomposition and constructing linear transformations.
Computational Complexity and Efficiency
The outer product of two vectors generates a matrix with a computational complexity of O(mn) for vectors of sizes m and n, making it more resource-intensive than the inner product, which computes a scalar with O(n) complexity for vectors of length n. Inner products are generally more efficient in algorithms requiring scalar results, such as projections and distance calculations. Outer products are essential in constructing higher-dimensional matrices but may incur higher memory and computation costs, impacting efficiency in large-scale applications.
Practical Examples in Engineering and Science
The inner product, often realized as the dot product, is essential in engineering and science for calculating work done by a force in physics, where it measures the projection of force along displacement vectors. The outer product generates a matrix representing linear transformations or tensor products, crucial in computer graphics for rotations and in quantum mechanics to describe state vectors. Understanding the distinction allows engineers and scientists to apply vector and matrix operations effectively in simulations, signal processing, and the analysis of multidimensional data.
Summary and Key Takeaways
The outer product of two vectors produces a matrix representing all possible multiplications between vector components, useful for constructing higher-dimensional data representations and matrices. The inner product results in a scalar value representing the sum of pairwise multiplications, often used to measure similarity or projection in vector spaces. Key takeaways include that the outer product expands dimensionality and captures pairwise interactions, while the inner product provides a measure of alignment or correlation between vectors.
Outer product Infographic
 libterm.com
libterm.com